FFT
Die FFT („Fast Fourier Transformation“) ist ein Algorithmus zur Analyse von Signalen im Frequenzbereich.
Aufteilung des Signals nach Frequenzen
Wir gehen ab jetzt davon aus, dass wir mehrere Signale unterschiedlicher Frequenz, Amplitude und Phasenlage überlagert im digitalen Signal vorliegen haben. Das kann z. B. folgendermaßen aussehen, wenn die Zahlen im Speicher (120 Speicherstellen) dargestellt werden:
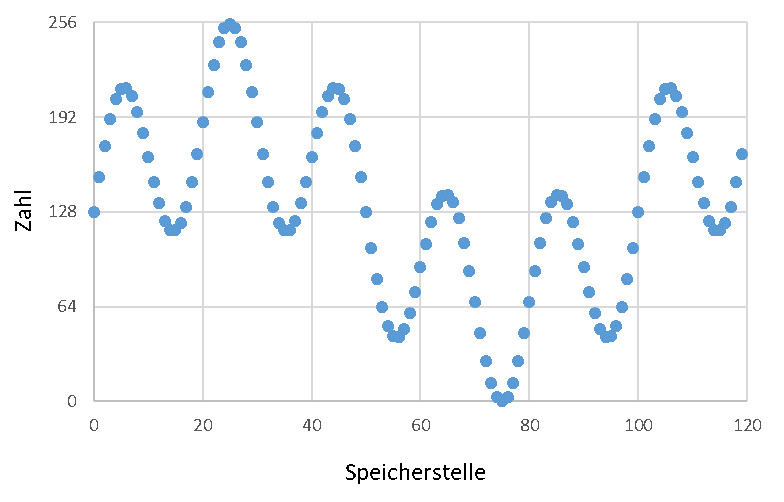
Dieser Zahlenstrom steht dem FFT-Algorithmus als Eingangsgröße zur Verfügung. Der FFT-Algorithmus gibt als Ergebnis Spitzenwert und Phase zu definierten Frequenzen aus. Wir gehen dabei davon aus, dass sich die Frequenz eines Signalanteils über der Zeit nicht ändert. Damit können wir Anteile des Signals über ihre Frequenz identifizieren. Die Frequenz ist viel besser als der Zeitverlauf dazu geeignet, die Signale voneinander zu separieren und dann zu analysieren. Nach Frequenzen getrennt sieht der obere Zeitverlauf folgendermaßen aus:
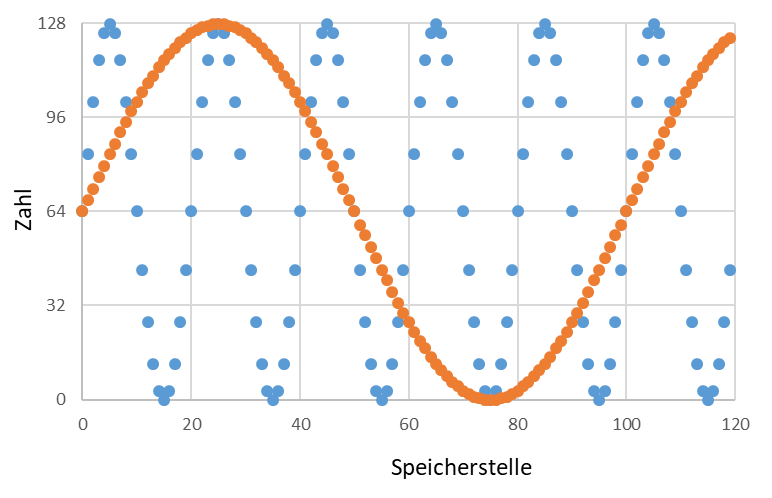
Werden diese beiden Signale addiert, erhalten wir wieder das ursprüngliche Signal. Nachdem der FFT-Algorithmus die Aufspaltung des Signals in die unterschiedlichen Frequenzen vollzogen hat, ist die Ermittlung der Signalparameter Spitzenwert und Phase einfacher möglich. Die Frequenzen geben Sie dem Algorithmus vor. Wie funktioniert das?
Ermittlung des Spitzenwertes
Der FFT-Algorithmus ist ein auf geringe Rechenzeit optimierter Algorithmus, der deshalb aus seinem Code heraus schwierig nachvollziehbar ist. Stattdessen gehen wir der prinzipiellen Funktionsweise der Fourier-Transformation auf den Grund.
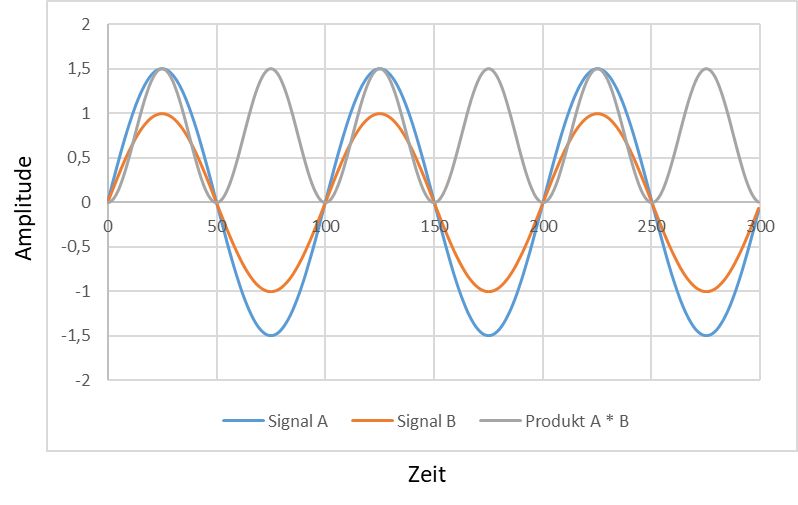
Werden zwei Signale A(t) = A0 ∙ sin (2π ∙ fA ∙ t) und B(t) = B0 ∙ sin (2π ∙ fB ∙ t) gleicher Frequenz fA = fB miteinander multipliziert, sieht das Ergebnis folgendermaßen aus:
Werden zwei Signale A(t) = A0 ∙ sin (2π ∙ fA ∙ t) und B(t) = B0 ∙ sin (2π ∙ fB ∙ t) unterschiedlicher Frequenz fA ≠ fB miteinander multipliziert, sieht das Ergebnis folgendermaßen aus:
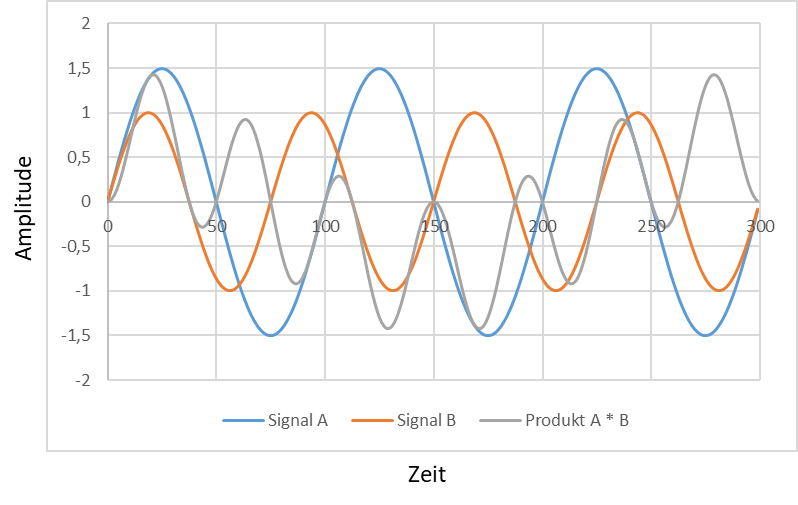
Das graue Signal aus A ∙ B ist in der oberen der beiden Abbildungen nur positiv. In der unteren Abbildung ist es mal positiv und mal negativ. Der Mittelwert des Produkts der Signale ist in der oberen Abbildung eine positive Zahl. Zu jeder Zeit ist das Produkt A ∙ B positiv. In der unteren Abbildung heben sich positive und negative Signalanteile in A ∙ B genau gegenseitig auf, so dass der Mittelwert 0 ist. Wir vereinfachen hier zunächst, dass beide Signale die gleiche Phase haben, also zeitlich nicht zueinander verschoben sind.
Die zentrale Aussage lautet:
Der Mittelwert des Produkts zweier Signale mit unterschiedlicher Frequenz ist gleich 0.
Der Mittelwert des Produkts zweier Signale mit gleicher Frequenz entspricht dem Term A0 ∙ B0 / 2.
Es gilt als Formel:
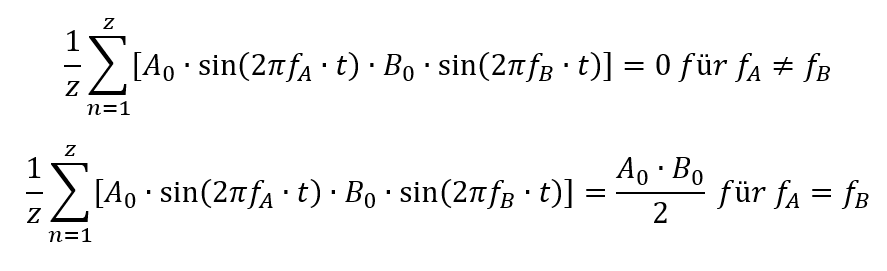
Der Parameter t für die Zeit in analogen Signalen wird bei digitalen Signalen zu einem Zähler n. Das sinusförmige abgetastete zeitdiskrete Signal A(t) wird als A(n) aus dem Speicher gelesen. Ein sinusförmiges Signal, das mit 20 Abtastwerten pro Periode digitalisiert worden ist, liegt folgendermaßen im Speicher vor:
| n | A(n) |
|---|---|
| 0 | 128 |
| 1 | 167 |
| 2 | 202 |
| 3 | 231 |
| 4 | 249 |
| 5 | 255 |
| 6 | 249 |
| 7 | 231 |
| 8 | 202 |
| 9 | 167 |
| 10 | 128 |
| 11 | 88 |
| 12 | 53 |
| 13 | 24 |
| 14 | 6 |
| 15 | 0 |
| 16 | 6 |
| 17 | 24 |
| 18 | 53 |
| 19 | 88 |
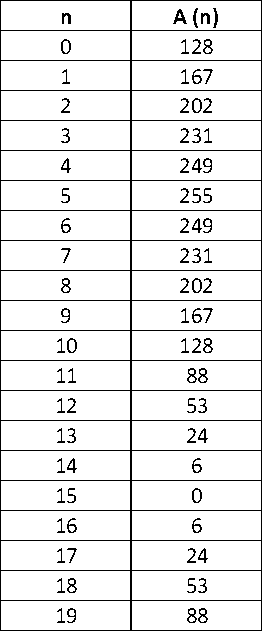
Es gilt also
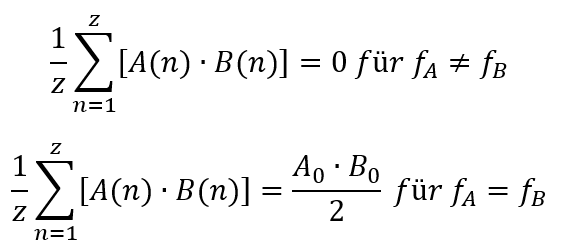
In vielen Anwendungen wissen wir, in welchem Bereich Frequenzen liegen, die im Signal vorhanden sind. Wenn wir z. B. die Spannung an der Steckdose messen, dann wissen wir, dass die Frequenz f = 50 Hz beträgt. Bei der Leitfähigkeitsmessung aus dem vorherigen Kapitel erzeugen wir ein Signal mit f = 1 kHz. Auch da wissen wir, dass Spannung und Strom beide die Frequenz f = 1 kHz haben. Wir können also testen, ob ein Signal bei einer bestimmten Frequenz vorhanden ist, und wie hoch dessen Spitzenwert ist. Dafür müssen wir das Signal nur mit einem Testsignal mit der Frequenz multiplizieren, bei der wir ein Signal erwarten.
Zurück zum Beispiel der Leitfähigkeitsmessung: Um zu ermitteln, welcher Spitzenwert bei 1 kHz im digitalen Datenstrom der Spannung U enthalten ist, multiplizieren wir den Datenstrom mit einem Testsignal T mit der Frequenz fT = 1 kHz und dem Spitzenwert T0 = 1:
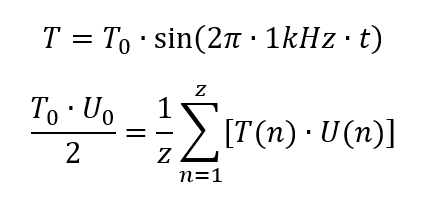
Das Spannungssignal U(n) kommt aus dem ADC. Das Testsignal wird von uns vorgegeben, also können wir es optimieren. Bei T0 = 1 vereinfacht sich das Ergebnis zu
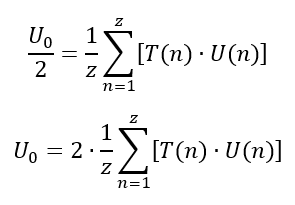
Mit dieser Formel können wir den Spitzenwert U0 des Signals ermitteln, das als Datenstrom im Speicher abgelegt ist.
Wir betrachten als Beispiel 20 Zahlen für U(n), die nacheinander vom ADC abgetastet worden sind. Der Spitzenwert von U (blau) ist hier 5. Wir betrachten zusätzlich das Testsignal T(n) mit dem Spitzenwert 1 (rot). Die Frequenzen von U und T sind gleich gewählt.
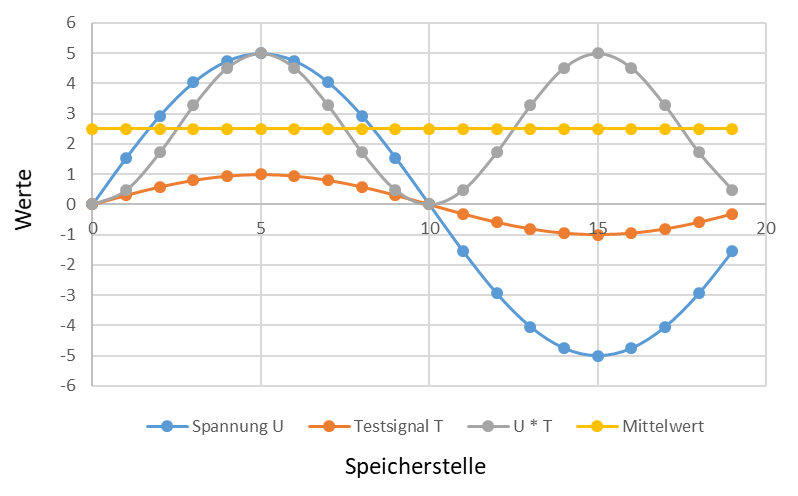
In grau sehen Sie den Verlauf von U(n) ∙ T(n) und in gelb den Mittelwert des grauen Signals. Es gilt
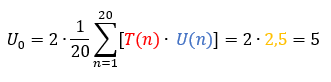
In der Tabelle unten sehen Sie die zugehörigen Daten aus Excel. Der Mittelwert ganz unten ist der Mittelwert der Zahlen in der rechten Spalte.
| n | U(n) | T(n) | U(n) · T(n) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1,54508497 | 0,30901699 | 0,47745751 |
| 2 | 2,93892626 | 0,58778525 | 1,72745751 |
| 3 | 4,04508497 | 0,80901699 | 3,27254249 |
| 4 | 4,75528258 | 0,95105652 | 4,52254249 |
| 5 | 5 | 1 | 5 |
| 6 | 4,75528258 | 0,95105652 | 4,52254249 |
| 7 | 4,04508497 | 0,80901699 | 3,27254249 |
| 8 | 2,93892626 | 0,58778525 | 1,72745751 |
| 9 | 1,54508497 | 0,30901699 | 0,47745751 |
| 10 | 6,1257E-16 | 1,2251E-16 | 7,5049E-32 |
| 11 | -1,54508497 | -0,30901699 | 0,47745751 |
| 12 | -2,93892626 | -0,58778525 | 1,72745751 |
| 13 | -4,04508497 | -0,80901699 | 3,27254249 |
| 14 | -4,75528258 | -0,95105652 | 4,52254249 |
| 15 | -5 | -1 | 5 |
| 16 | -4,75528258 | -0,95105652 | 4,52254249 |
| 17 | -4,04508497 | -0,80901699 | 3,27254249 |
| 18 | -2,93892626 | -0,58778525 | 1,72745751 |
| 19 | -1,54508497 | -0,30901699 | 0,47745751 |
| Mittelwert | 2,5 | ||
Anwendung auf viele Frequenzen
Die FFT führt diese Rechnung (sehr stark optimiert) für viele Frequenzen durch, die eine konstanten Abstand zueinander haben. Sie geben dabei die unterste Frequenz, die oberste Frequenz und die Anzahl der Frequenzen gleichen Abstands dazwischen an. Das folgende Beispiel zeigt ein Signal mit zwei Frequenzanteilen:
Es gilt
U (n) = 3 ∙ sin(2π 100Hz ∙ n) + 1,5 ∙ sin(2π 300Hz ∙ n)
Wir multiplizieren nacheinander Testsignale
T1 (n) = 1 ∙ sin(2π 100Hz ∙ n)
T2 (n) = 1 ∙ sin(2π 200Hz ∙ n)
T3 (n) = 1 ∙ sin(2π 300Hz ∙ n)
T4 (n) = 1 ∙ sin(2π 400Hz ∙ n)
mit dem Spannungssignal U(n). Das Ergebnis lautet:
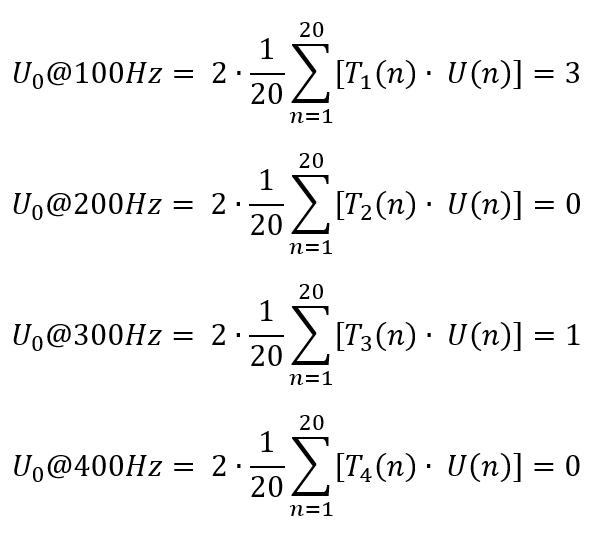
Die Spitzenwerte werden also korrekt ermittelt. Die klassische Darstellung der Spitzenwerte bei unterschiedlichen diskreten Frequenzen sieht folgendermaßen aus:
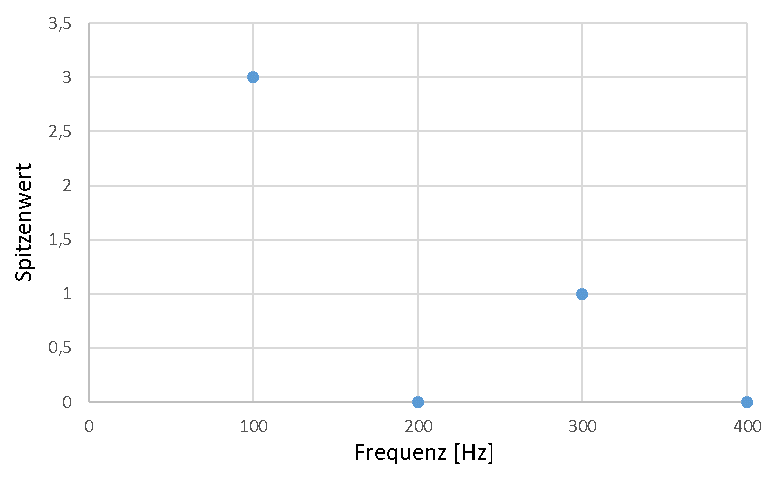
Sie können im Excel-Sheet unten versuchen, diese Frequenzanalyse selbstständig zu programmieren.
Übung zu Fourier-Transformation (Excel)
Phasen
Bisher hatten wir vereinfacht, dass die Phasen aller Signale 0 sind. Alle Signalanteile sind zueinander also nicht zeitlich verschoben. Das ist in realen Messsignalen aber nicht der Fall. Deshalb brauchen wir eine allgemeinere Lösung. Um Spitzenwerte und Phasen zu ermitteln, multiplizieren wir das Eingangssignal pro Test-Frequenz mit zwei Testsignalen, die um 90° oder π / 2 zueinander phasenverschoben sind:
TSin = 1 ∙ sin(2π ∙ f ∙ t)
TCos = 1 ∙ cos(2π ∙ f ∙ t)
Sie erhalten damit Realteil und Imaginärteil des Eingangssignals bezogen auf die Phase des Testsignals. Es gilt
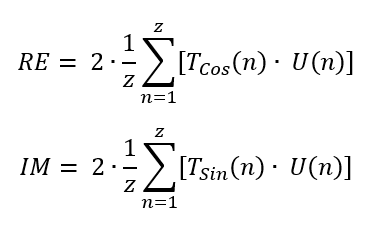
Spitzenwert und Phase berechnen Sie mit
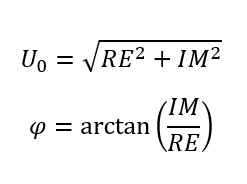
Aufgabe: Verschieben Sie einen Signalanteil einer Frequenz im Excel-Beispiel in der Phase. Programmieren Sie die Auswertung so, dass Phase und Spitzenwert aller Frequenzanteile richtig errechnet werden.