Schwingfähige Systeme mit zwei Speichern und mindestens einem Begrenzer werden als PT-2 Systeme bezeichnet. Allgemein weisen diese Systeme folgende Übertragungsfunktion auf:
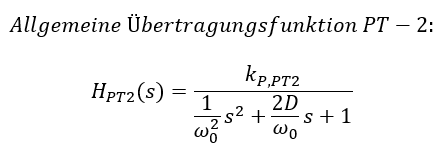
Der Parameter kP,PT2 im Zähler gibt die statische Verstärkung des Systems an. Im Nenner stehen die Parameter Resonanzfrequenz „ω0“ und Dämpfung „D“. Die komplexe Frequenz s stellt im Frequenzbereich immer die veränderliche Größe dar. Im eingeschwungenen Zustand bei s = 0 gilt:
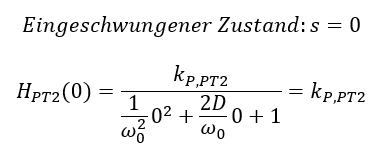
Systeme mit PT-2-Verhalten können schwingen oder auch nicht. Dämpfung und Resonanzfrequenz dieser Systeme hängen von der Parametrierung der Funktionsblöcke ab. Über die Parametrierung des Reglers können wir Dämpfung und Resonanzfrequenz i. A. beeinflussen.
Es werden folgende Fälle für die Dämpfung unterschieden:
D = 0: Kontinuierliche ungedämpfte Schwingung
0 < D < 1: Abklingende Schwingung
D = 1: Aperiodischer Grenzfall: Gerade so keine Schwingung
D > 1: Nicht schwingendes System
Um ein PT-2-System zu analysieren führen wir einen Koeffizientenvergleich durch. Wir setzen die allgemeine Gleichung des Verhaltens gleich der speziellen Gleichung des betrachteten Systems. Das zeige ich an folgendem Beispiel. Dafür nehmen wir ein System mit PT-1 Verhalten und I-Verhalten hintereinander geschaltet in einem Regelkreis. Parameter A besteht also aus I-Verhalten und PT-1-Verhalten. Zur Vereinfachung setzen wir τ des Systems zu 1:

Der Parameter kI bildet zusammen mit dem Integrator 1/s das I-Verhalten ab. Es folgt ein Funktionsblock mit PT-1-Verhalten, der im Beispiel mit KP = 1 und τ = 1 modelliert ist. Der Wert der Dämpfung D hängt von Parameter kI ab. Damit das System „leicht“ schwingt, setzen wir zunächst kI = 10.
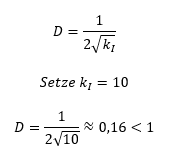
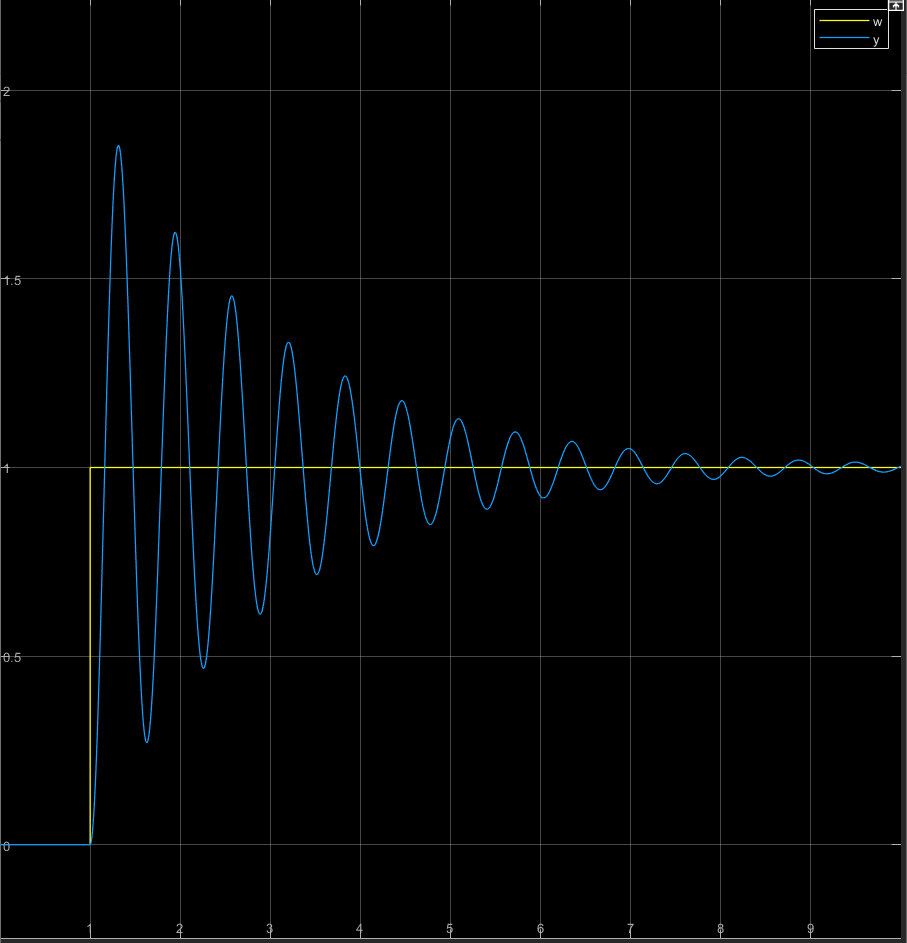
Die Dämpfung D ist kleiner als 1, also schwingt das System. Sie ist aber größer als 0, deshalb schwingt es nicht dauerhaft. Es verhält sich wie eine Schaukel, die aufgrund der Reibung langsamer wird. Die Sprungantwort zeigt typisches schwingfähiges PT-2 Verhalten mit leichtem „Überschwingen“. Die Regelgröße schwingt über die Führungsgröße hinaus und pendelt dann um den Wert der Führungsgrößer herum. Die Schwingung ist abklingend, so dass irgendwann die Regelgröße den Wert der Führungsgröße erreicht.
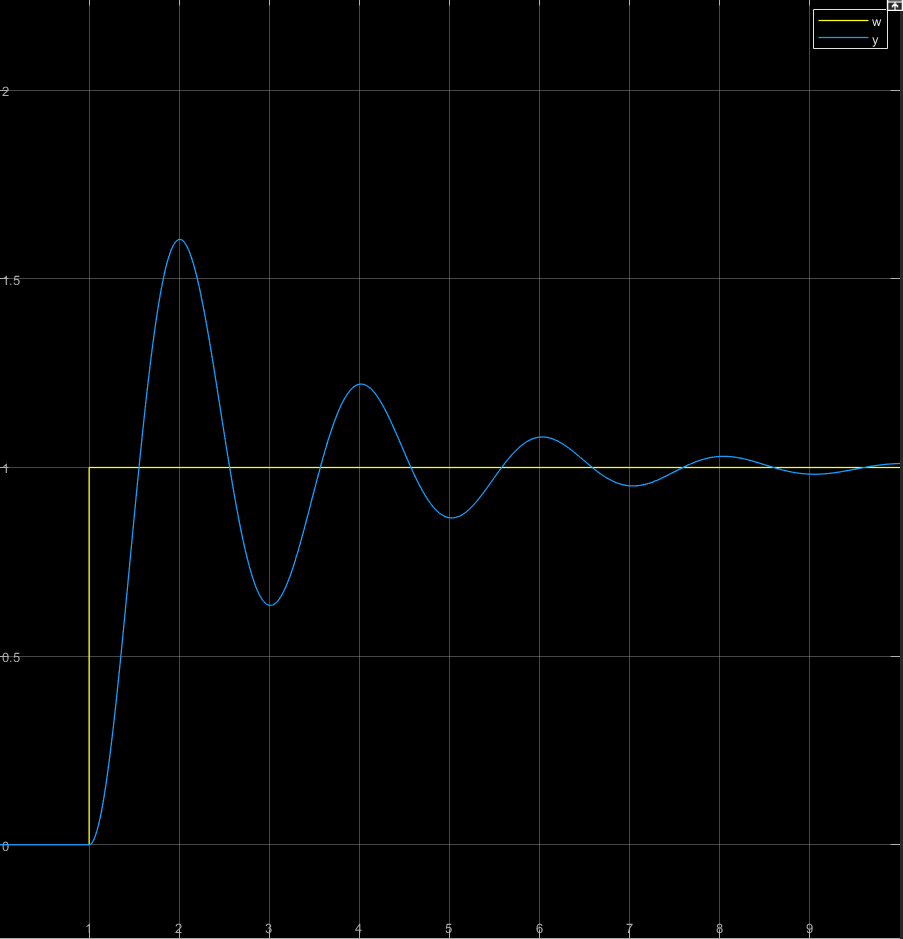
Die Regelgröße erreicht die Führungsgröße zum ersten Mal bereits nach ca. 0,5s. Das ist ziemlich schnell verglichen mit nicht schwingenden PT-2-Systemen. Der charakteristische Parameter ω0 gibt die Kreisfrequenz der abklingenden Schwingung an. Wir ermitteln die Schwing-Kreisfrequenz aus der Grafik über die Periodendauer. Sie ist als Zeit zwischen zwei Maxima der abklingenden Schwingung definiert.

Die Berechnung stimmt mit dem abgelesenen Wert ziemlich gut überein. Die Schwingung klingt ab, so dass wir nach längerer Zeit den eingeschwungenen Zustand erreichen. Hier gilt y = 1.
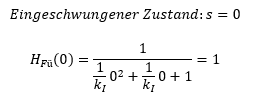
Das Überschwingen charakterisieren wir folgendermaßen: Der maximale Wert der Regelgröße beträgt ca. y = 1,7 bei t = 2s (Sekunden). Die Führungsgröße springt auf w = 1. Damit schwingt die Regelgröße um 70% über den Wert der Führungsgröße über.
Die Dämpfung D können wir aus der Grafik nur schwierig ablesen. Dafür gibt es zwar auch Formeln, aber die sind recht ungenau und komplex zu rechnen.
Wir können durch Änderung des Parameters KI das Verhalten des Systems ändern. Mit größerem KI sinkt die Dämpfung und die Schwingfrequenz steigt. Das zeigt folgende Simulation für KI = 100:

Die Regelgröße erreicht die Führungsgröße zum ersten Mal bereits nach ca. 0,2s. Das Überschwingen steigt aufgrund der geringeren Dämpfung von D = 0,05 auf ca. 80% an. Die Resonanzfrequenz ist größer geworden.
Der aperiodische Grenzfall mit D = 1 wird oft angestrebt, weil er den schnellsten möglichen Anstieg der Regelgröße ohne Überschwingen darstellt. Im Beispielsystem brauchen wir dafür
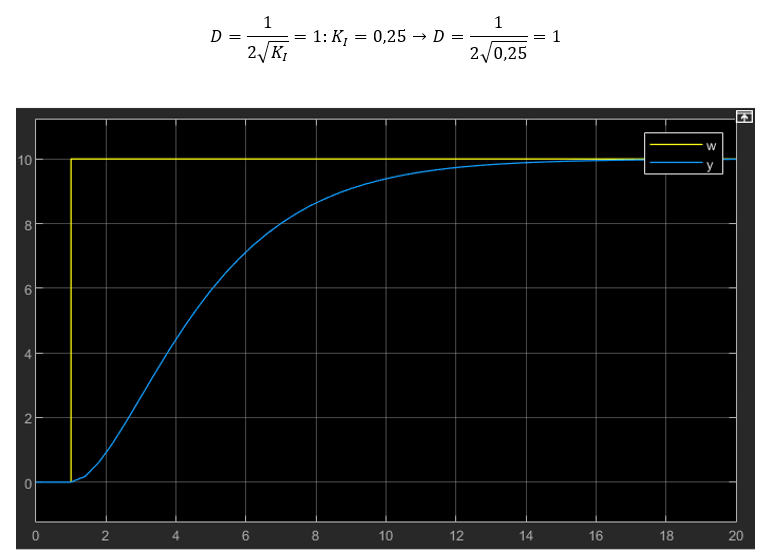
In der Sprungantwort ist die Simulationsdauer auf 20 verdoppelt worden, damit das Einschwingen noch dargestellt werden kann. Die Zeit, bis das System seinen eingeschwungenen Zustand erreicht, ist bei größerer Dämpfung (D = 1 statt D = 0,16) deutlich größer geworden. Dafür schwingt die Regelgröße nicht über.
Auswirkungen von Überschwingen
Beim Überschwingen übersteigt die Regelgröße den maximalen vorgesehenen Wert. Überschwingen ist in Regelkreisen oft problematisch, weil dadurch Komponenten kurzzeitig stärker belastet werden als geplant. Dadurch können die Komponenten beschädigt werden.
In einem Druckregelkreis herrscht z. B. ein maximaler Soll-Druck von 10 bar. Wenn das geregelte System aber um 80% überschwingt, dann können kurzzeitig Drücke von 18 bar auftreten. Das müssen die Komponenten aushalten können. Diese Überdimensionierung kostet Geld.
Parameteroptimierung
Vergleichen wir die drei bisher betrachteten Fälle. Im aperiodischen Grenzfall mit D = 1 ist die Ausgangsgröße träge. Es dauert lange, bis sie den Wert der Führungsgröße erreicht. Dafür schwingt die Regelgröße nicht über.
Bei kI = 10 gilt D = 0,16. Die Regelgröße schwingt um ca. 70% über. Dafür erreicht die Regelgröße den Endwert schneller. Bei kI = 100 und D = 0,05 schwingt die Regelgröße um ca. 80% über. Dafür erreicht die Regelgröße den Wert der Führungsgröße noch schneller.
Je größer die Verstärkung in einem Regelkreis mit 2 Speichern gewählt wird, desto schneller erreicht die Regelgröße den Wert der Führungsgröße. Die Resonanzfrequenz wird größer. Die Regelgröße schwingt stärker über. Hier müssen wir einen Kompromiss für die Applikation finden. Wir können nicht alles gleichzeitig erreichen. Ein System ohne Überschwingen ist langsamer als möglich.
Ein träges System reagiert langsam auf Veränderungen. Während der Übergangszeit bis zum eingeschwungenen Zustand weicht die Regelgröße teilweise deutlich von der Führungsgröße ab. Wenn Trägheit und temporäre Regelabweichung kein Problem für die Anwendung darstellen, dann sollten Sie am Regler den aperiodischen Grenzfall mit D = 1 einstellen.
Ein Beispiel dafür ist der Tempomat am Auto. Es darf ruhig einige Sekunden dauern, bis die Geschwindigkeit sich auf einen neuen Geschwindigkeitswunsch eingestellt hat. Anders herum wäre es ziemlich ärgerlich, wenn die Geschwindigkeit kurzzeitig um 50% über den Sollwert hinausschießt. Deshalb wird hier der aperiodische Grenzfall angestrebt.
Bei einer Werkzeugmaschine geht die Welt nicht unter, wenn die Drehzahl eines Bohrers mal um 50% zu hoch ist. Sie ist aber darauf angewiesen, die Drehzahl sehr schnell ändern zu können. Wenn die Maschine 100 Löcher pro Minute in die Bretter eines Ikea-Schranks bohren soll, dann muss der Bohrer ziemlich schnell reagieren. Hier würde man D zwischen 0 und 1 legen, damit die Einschwingzeit kurz ist.
Erweiterung der Ziele
Für einen Regelkreis werden die Ziele folgendermaßen erweitert:
1. Es sollte gelten: HFü = 1
2. Das System sollte nach möglichst geringer Zeit eingeschwungen sein, also seinen Endwert erreicht haben.
3. Das Überschwingen soll auf einen maximalen Wert begrenzt werden. Das System soll nicht dauerhaft schwingen.
Weiter