Die Physik der Bauelemente gibt uns folgende Gleichungen für die Berechnung von Spannung und Strom. Die Gleichungen sind das Ergebnis der LaPlace-Transformation.
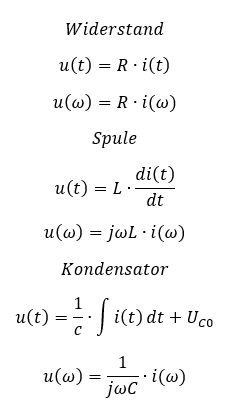
Diese Gleichungen geben an, wie groß eine Spannung an einem Bauelement ist, wenn der Strom bekannt ist. Oder wir nutzen Sie anders herum zur Berechnung eines Stroms, wenn die Spannung bekannt ist.
Die drei Bauelementgleichungen ähneln sich stark. Wir nutzen die Ähnlichkeit und definieren eine komplexe Impedanz Z(ω), mit der wir Spannung und Strom immer auf die gleiche Weise berechnen können: Es gilt immer u(ω) = Z(ω) ∙ i(ω). Dies wird auch als komplexes Ohm´sches Gesetz bezeichnet, denn es ist u(t) = R ∙ i(t) ähnlich. Wir definieren komplexe Impedanzen für die Bauelemente so, dass das komplexe Ohm´sche Gesetz gilt:

Eine Impedanz ist ein Wechselstrom-Widerstand. Er gibt an, wie viel Widerstand ein Bauelement dem Wechselstrom entgegensetzt. Bei größerer Impedanz fließt weniger Strom. Mit Impedanzen rechnen Sie wie mit Widerständen.
Wir definieren die komplexe Impedanz vor allem, damit wir mit Wechselstrom genauso einfach rechnen können wie mit Gleichstrom. Es handelt sich um eine mathematische Vereinfachung. Sie beschreibt aber auch das Verhalten der Bauelemente bei Wechselstrom in der Denkweise der komplexen Rechnung. Das möchte ich Ihnen nahebringen, weil es dem Verständnis dient.
Bedeutung von j und ω
Strom und Spannung an Speichern hängen mathematisch über j und ω zusammen. Mit der Definition von komplexen Impedanzen werden die Größen j und ω in die Bauelementgleichung verschoben. Sie kommen erst durch die Bauelemente ins Spiel, deshalb gehören sie da auch hin. Die Netzwerkgleichungen bleiben mit diesem Trick genauso wie bei Gleichstrom. Bei Wechselstrom gilt z. B. die gleiche Stromteiler-Regel wie bei Gleichstrom. Nur setzen wir statt Widerstandswerten R komplexe Impedanzen Z ein.
Der Parameter ω = 2πf ist eine Frequenz. Je größer die Frequenz f einer Wechselspannung ist, die an einem Bauelement anliegt, desto größer ist auch ω. Wenn die Impedanz eines Bauelements den Parameter ω enthält, dann ändert sich der Wechselstrom-Widerstand mit der Frequenz der Spannung, die am Bauelement anliegt.
Der Faktor ∙j dreht die Phase um 90° gegen den Uhrzeigersinn. Im Zeitbereich verschiebt er damit ein Wechselsignal zeitlich nach links. Das Signal ist also zeitlich voraus. Die Winkelverschiebung um π/2 oder 90° ist mit einer Zeitverschiebung um eine Viertel Periodendauer verknüpft. Wie lange eine Periode dauert hängt davon ab, wie hoch die Frequenz des Signals ist (T = 1/f). Also verschiebt die Multiplikation mit ∙j ein Signal um T/4 zeitlich nach vorne (nach links). Ein Signal kann eine Spannung oder ein Strom sein, je nachdem vor welcher Größe das j auftaucht.
Der Faktor ∙(-j) dreht die Phase um 90° im Uhrzeigersinn. Im Zeitbereich entspricht das einer Verschiebung des Signals um T/4 hinter die Spannung (nach rechts).
Der Widerstand dreht die Phase gar nicht, seine Impedanz ist rein reell. Die Spulenimpedanz beinhaltet Faktor j. Die Kondensatorimpedanz weist Faktor 1/j = -j auf. Speichernde Bauelemente drehen immer die Phase von Spannung und Strom relativ zueinander um ±j.
Im Rest des Kapitels betrachten wir einfache Beispielaufgaben für das Rechnen mit Impedanzen. Es wird jeweils eine Impedanz zu einem der drei Bauelemente berechnet. Anschließend wird bei einer Wechselspannung der Wechselstrom durch das Bauelement berechnet.
Widerstand
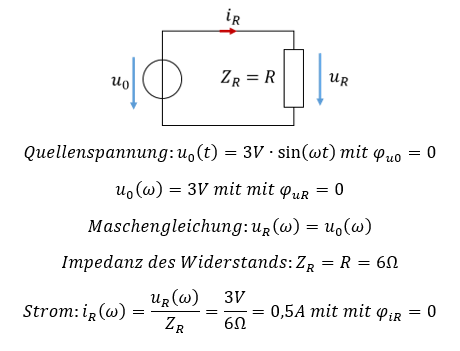
Wir beginnen mit dem Ohm´schen Widerstand mit R = 6Ω. Der Widerstand wird an einer idealen Wechselspannungsquelle betrieben. Liegt der Widerstand parallel zur Quelle, liegt an ihm die Spannung uR = u0 an. Die Maschengleichung gilt bei Gleichstrom und bei Wechselstrom.
In der unteren Abbildung sehen Sie oben den Zeitverlauf von Spannung und Strom am Widerstand. Es wird deutlich, dass keine Phasenverschiebung vorliegt. Darunter sehen Sie die komplexe Spannung und den komplexen Strom. Er wird nicht über der Zeit t, sondern über der Kreisfrequenz ω aufgetragen. Strom und Spannung sind in dieser Darstellung Punkte. Ganz unten sehen Sie die Phase von Strom und Spannung über der Kreisfrequenz ω aufgetragen. Auch die Phase ist jeweils ein Punkt im Diagramm.
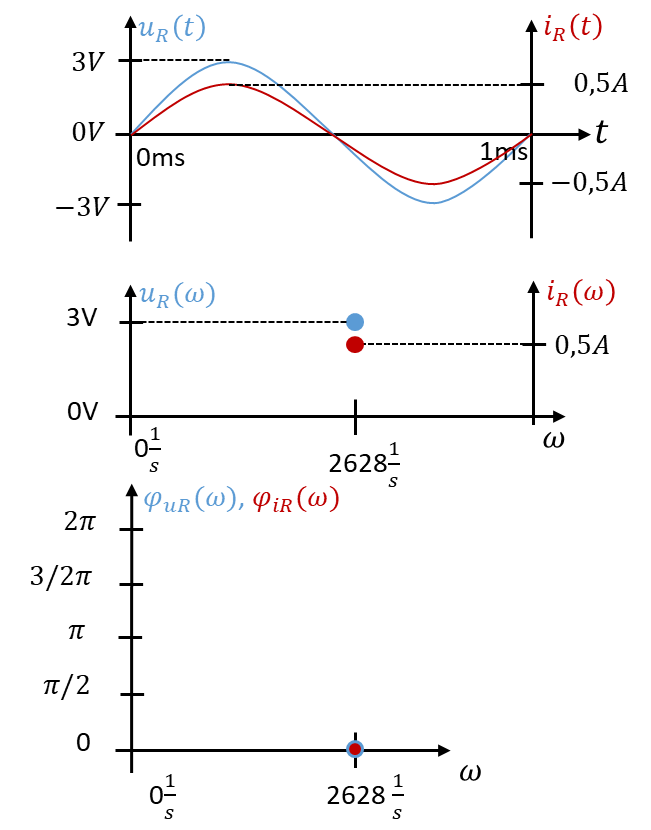
In der oberen Abbildung sind die Verläuft von Spannung und Strom gleichzeitig in einem Grafen dargestellt. Da Strom und Spannung unterschiedliche y-Achsen mit unterschiedlichen Einheiten sind, muss dafür jeweils eine eigene Y-Achse gezeichnet werden. Die roten Verläufe des Stroms gelten also für die Strom-Achse, die blauen der Spannung für die Spannungs-Achse. Die x-Achse (Zeitachse) gilt für beide Verläufe. In der untersten Grafik sind die Phasen für Spannung und Strom gleich. Damit man beide sehen kann ist der Punkt der Stromphase etwas kleiner als der der Spannungsphase dargestellt.
Kondensator
Wir legen jetzt die gleiche Spannung u0 an einem Kondensator mit C = 1mF an. Zunächst berechnen wir die Impedanz des Kondensators. Dafür ist die Frequenz f wichtig. Wir betreiben die Schaltung im Beispiel bei f = 1kHz. Es gilt
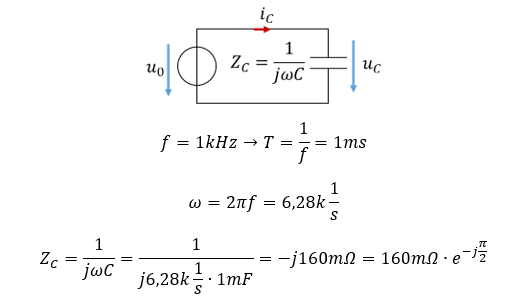
Zur Erinnerung: Es gilt 1/j = -j. Da eine Impedanz immer den Quotienten aus Spannung und Strom abbildet, muss jede Impedanz die Einheit Ω haben. Die Impedanz eines Kondensators ist immer negativ. Für den Strom gilt:
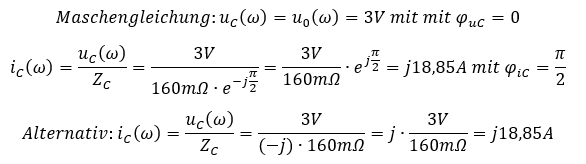
Der Strom ist gegenüber der Spannung um π/2 im Zeitverlauf nach links verschoben. Der Strom eilt der Spannung voraus. Der Spitzenwert des Stroms beträgt 18,85A. Er hängt vom Term ωC der Impedanz ab. Der Spitzenwert des Stroms am Kondensator ist also auch eine Funktion der Frequenz. Der Strom steigt mit steigender Frequenz linear an.
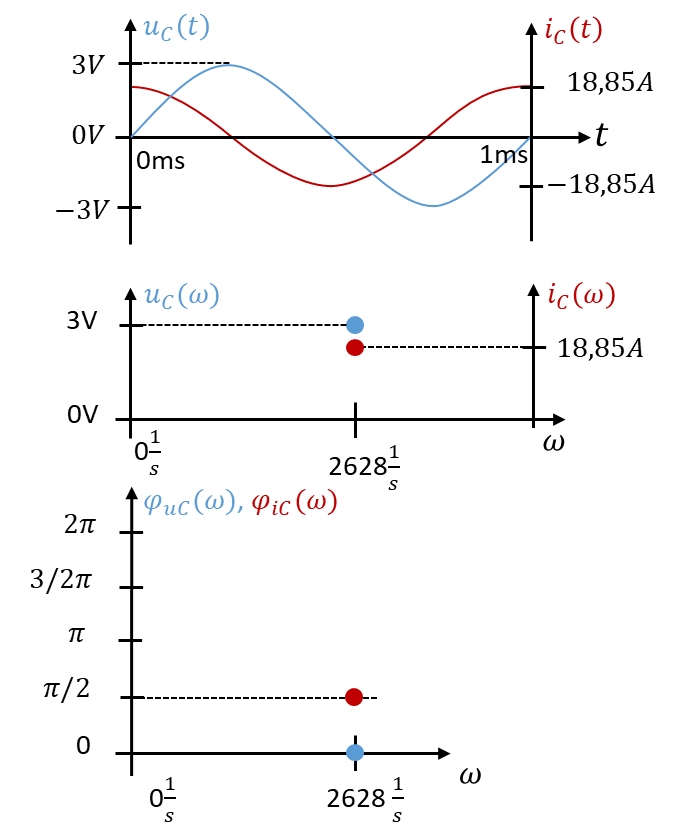
Die Parameter j und ω werden für die Berechnung der Spulenimpedanz verwendet. Die Kreisfrequenz ω geht in den Zahlenwert der Impedanz ein und ist anschließend nicht mehr in den Formeln sichtbar. Der Parameter j wird bei den weiteren Berechnungen mitgenommen.
Spule
Wir betreiben die Quelle jetzt an einer Spule. Berechnen wir als nächstes die Impedanz einer Spule mit L=5mH. Dann berechnen wir den zugehörigen Strom aus Spannung und Impedanz:
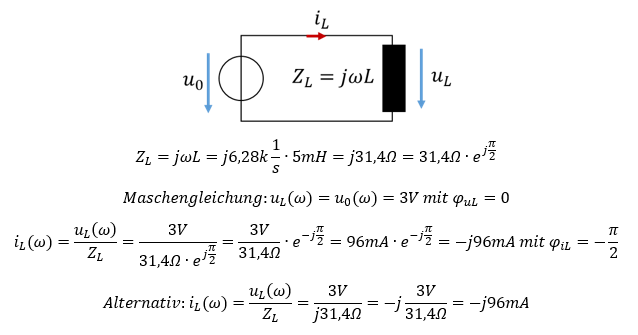
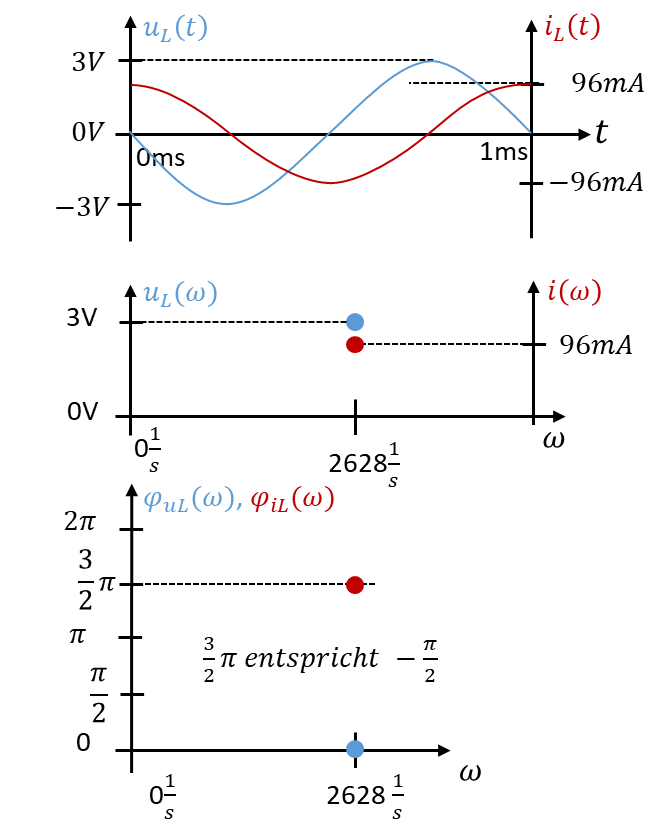
Auch an der Spule ist der Strom abhängig von der Frequenz. Er sinkt bei konstanter Spannung mit steigender Frequenz f.
Weiter