Ein System, dessen Ausgang den Eingang ableitet, weist „D-Verhalten“ auf. Das „D“ steht für Differenzierung oder Differenzial. D-Verhalten oder differenzierendes Verhalten liegt in der Praxis selten vor. Wenn Sie bei einem System mit I-Verhalten Eingang und Ausgang vertauschen, dann erhalten Sie die Umkehrfunktion der ursprünglichen Übertragungsfunktion als neue Übertragungsfunktion. Die Umkehrfunktion des Integrals ist die Ableitung. Wenn wir also z. B. bei einem Eimer den Zulauf als Ausgang und den Füllstand als Eingang definieren, dann weist das System D-Verhalten auf.
Ein gutes Beispiel ist die Fahrrad-Luftpumpe. Sie ist ein Tank mit vertauschtem Ein- und Ausgang. Der Eingang ist der Hub des Kolbens, den Sie mit der Hand bewegen. Er entspricht der Füllhöhe der Kompressionskammer der Pumpe. Durch die Bewegung des Kolbens wird die Höhe reduziert und es entweicht Luft aus dem Ausgang. Je schneller Sie den Kolben bewegen, desto mehr Luft entweicht aus dem Ausgang. Es gilt:

Wir nutzen wieder die LaPlace-Transformation, um die Ableitung zu umgehen. Die Übertragungsfunktion eines allgemeinen Blocks mit D-Verhalten lautet:
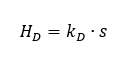
Der charakteristische Parameter zur Beschreibung von D-Verhalten lautet kD. Im Beispiel oben gilt kD = A (Fläche). Im Blockschaltbild wird ein Funktionsblock mit D-Verhalten folgendermaßen modelliert:
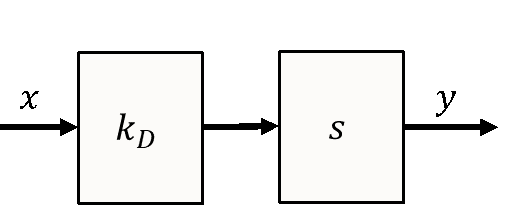
Immer wenn Sie in einem Blockschaltbild den Faktor s (nicht 1/s) sehen, wird D-Verhalten modelliert. Die Sprungantwort von D-Verhalten ist schwierig zu zeichnen. Wird ein idealer Sprung der Dauer 0s im Eingangssignal abgeleitet, ist das Ergebnis unendlich. Wir zeichnen die Sprungantwort folgendermaßen:
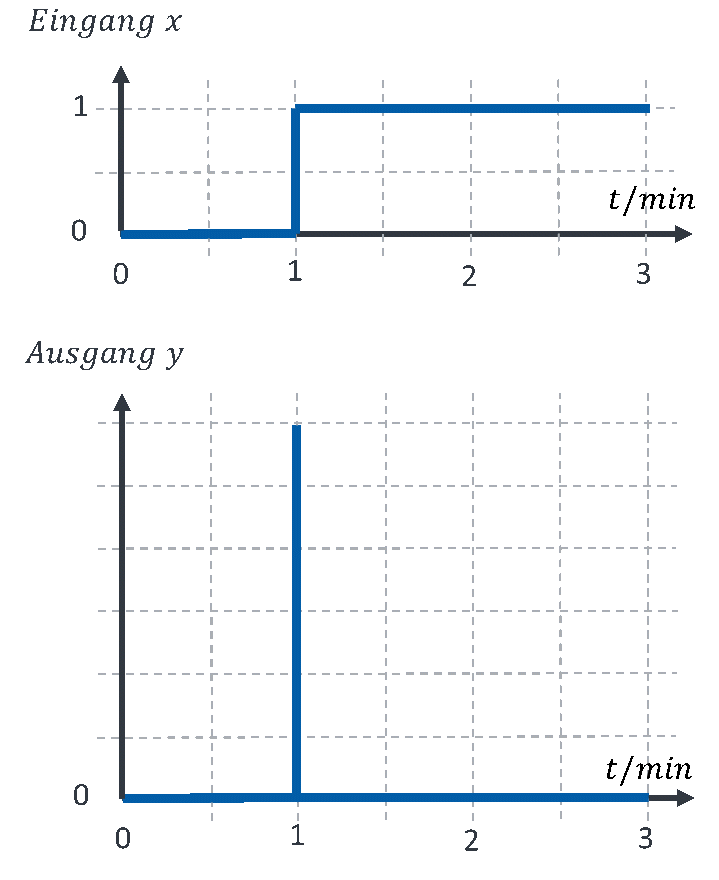
Während der Eingang konstant ist, ist der Ausgang = 0, denn die Ableitung eines konstanten Werts ist immer 0. Während des Sprungs ist die Steigung der Eingangsgröße unendlich hoch. Der Ausgang reagiert, indem er unendlich hochsteigt. In realen Systemen springt der Ausgang auf einen sehr hohen Wert, üblicherweise auf das physikalische Maximum des Ausgangs. Wie hoch das Maximum ist, ist bei jedem System unterschiedlich. Nach dem Sprung ist die Eingangsgröße wieder konstant. Die Ableitung am Ausgang ist wieder gleich 0.
Wir betrachten D-Verhalten nicht im Regelkreis, weil das den zeitlichen Rahmen des Tutorials sprengt. Tendenziell schwingt ein geregeltes System durch D-Verhalten schneller ein. Dafür wird es instabiler.
Weiter