Wenn Sie 10 Widerstände mit R=10kΩ nebeneinanderlegen und mit einem Multimeter vermessen stellen Sie fest, dass die Werte der Widerstände sich unterscheiden, obwohl der Hersteller sie alle mit der gleichen Bezeichnung verkauft. Es ist nicht möglich, unterschiedliche Dinge gleicher Bauart exakt identisch herzustellen, Sie müssen nur genau genug messen um überall Unterschiede festzustellen.
Initiale Genauigkeit
Bauelemente sind in Genauigkeitsklassen eingeteilt. Wenn Sie 10kΩ-Widerstände der 1%-Klasse kaufen, dann liegen die Werte um ±1% um den Sollwert von 10kΩ zwischen 9,9 kΩ und 10,1 kΩ. Es gibt auch Widerstände mit 0,1% Abweichung vom Sollwert und noch bessere. Je genauer der Widerstandswert, desto teurer der Widerstand. Die Verteilung der Werte folgt der Gauß-Verteilung aus der Stochastik. Dabei werden auf der Y-Achse die Anzahl der Widerstände und auf der X-Achse die Werte dargestellt. Wir betrachten dabei sehr viele Widerstände, die nominell den gleichen Wert haben sollten. Je mehr dieser Widerstände einen bestimmten Wert haben, desto größer ist der Wert auf der Y-Achse. Es wird deutlich, dass die meisten Werte in der Nähe des Sollwerts liegen und nur extrem wenige an den Bereichsgrenzen liegen. Siehe dazu hier.
Sie können sicher sein, dass der Wert eines Widerstands innerhalb des spezifizierten Bereichs (z. B: ±1% des Sollwerts) liegt. Wenn Sie den Wert eines Widerstands genauer wissen möchten, dann müssen Sie mit einem Multimeter seinen Wert nachmessen. Beachten Sie, dass es auch unterschiedlich genaue Multimeter gibt, die sind auch nicht ideal.
Alterung
Wenn Sie den Wert eines Widerstands ausreichend genau kennen, können Sie noch nicht sicher sein, dass er diesen Wert behält. Mit zunehmendem Alter ändert sich der Wert eines Widerstands. Diese Änderung wird üblicherweise in PPM/Jahr angegeben. PPM steht für Parts Per Million. Die Angabe 10PPM/Jahr bedeutet, dass sich der Wert pro Jahr um 10 Millionenstel des Sollwerts ändert. Sie berechnen die Widerstandsänderung ΔR eines Widerstand mit nominal 10kΩ mit der Formel

Nach 10 Jahren im Einsatz weicht der Widerstandswert vom Nominalwert um maximal ±0,01% ab. Ein Widerstand mit dem Nominalwert R = 10 kΩ ändert also seinen Wert um bis zu ±1Ω. Oft können wir diesen Effekt ignorieren, weil er so klein ist.
Temperaturabhängigkeit
Widerstände sind temperaturabhängig. Es wird die Änderung des Widerstandswerts pro °C angegeben. Ein Widerstand mit einem Temperaturkoeffizienten TK= 0,1%/°C ändert seinen Wert nach folgender Formel über der Temperartur:
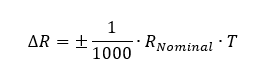
Wird unser 10kΩ-Widerstand z. B. im Motorraum eines Autos eingesetzt, muss er Temperaturen zwischen -40°C und 85°C aushalten können. Die Nominaltemperatur, für die er ausgelegt ist, beträgt 25°C. Es treten also im normalen Betrieb Änderungen von +60°C und -65°C auf. Das führt zu einer zusätzlichen Widerstandsänderung bei extrem kalten Temperaturen von
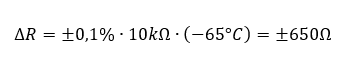
Diesen Effekt müssen wir bei der Auslegung von Schaltungen beachten. Es gibt natürlich für Geld auch Widerstände mit kleinerem Temperaturkoeffizienten am Markt.
Maximale Leistung
Elektrische Leistung erwärmt einen Widerstand. Diese Wärme muss er an seine Umgebung abgeben, sonst steigt seine Temperatur immer weiter an. Ab einer Grenztemperatur brennt der Widerstand und er wird zerstört. Widerstände werden in unterschiedlichen Leistungsklassen angeboten. Je größer (im Sinne der Geometrie, nicht im Sinne des Widerstandswerts) er ist, desto mehr Oberfläche hat er und desto mehr Wärme gibt er an die Umgebung ab.
Weiter