Alte Kurse › Antriebstechnik › Energieversorgung

Phasenwinkel und Leistungsfaktor

Zunächst müssen wir ermitteln, wie hoch Wirk- und Blindleistung an einem Verbraucher sind. Die Spannungen am Netz sind immer unveränderlich. Deshalb wird die Art der Leistung durch die Lastimpedanz bzw. den Laststrom bestimmt. Der Phasenwinkel φ aus der Wechselstromleistung beschreibt den Zusammenhang folgendermaßen:

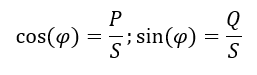
\[ \cos(\varphi) = \frac{P}{S};\; \sin(\varphi) = \frac{Q}{S} \]

Der Leistungsfaktor cos(φ) gibt an, wie hoch der Anteil der Wirkleistung an der Scheinleistung ist. Das Ziel ist Wirkleistung = Scheinleistung und Blindleistung = 0. Dafür muss gelten:

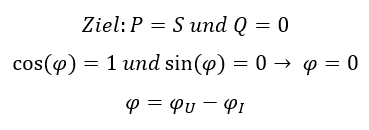
\[ \begin{gathered} \text{Ziel: } P = S \text{ und } Q = 0 \\[4pt] \cos(\varphi) = 1 \text{ und } \sin(\varphi) = 0 \rightarrow \varphi = 0 \\[4pt] \varphi = \varphi_U - \varphi_I \end{gathered} \]

Wenn der Phasenwinkel φ zwischen Spannung und Strom 0° beträgt, dann haben wir nur Wirkleistung im System. Dann sind Spannung und Strom in Phase und die Last verhält sich wie ein Ohm´scher Widerstand. Sobald im Verbraucher Spulen oder Kondensatoren auftauchen, fällt an diesen Bauelementen Blindleistung ab. Üblicherweise liegt also ein Mix aus Wirk- und Blindleistung an einem Verbraucher vor. Es gilt für Spannung, Strom und Phasenwinkel:

Zeitverläufe und Zeiger von Spannung (325 V, φu = 0) und Strom (5 A, φi = π/6); Phasenwinkel φ = φu − φi = −π/6

Die Zeitverläufe im Beispiel oben sind willkürlich gewählt, sie sind nicht allgemeingültig. Die Berechnung der Phase φ aus den Phasen von Spannung und Strom ist allgemein so wie oben beschreiben gültig. Bei Maschinen und Anlagen mit hoher Leistung muss für den Leistungsfaktor gelten:

\[ \cos(\varphi) \geq 0{,}95 \]

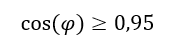
Die allgemeine Formel (inklusive Herleitung) zur Berechnung der Phase zwischen Spannung und Strom am Netz mit der Lastimpedanz Z lautet:

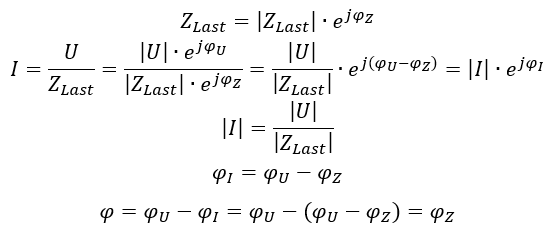
\[ \begin{gathered} Z_{\mathrm{Last}} = |Z_{\mathrm{Last}}| \cdot e^{j\varphi_Z} \\[6pt] I = \frac{U}{Z_{\mathrm{Last}}} = \frac{|U| \cdot e^{j\varphi_U}}{|Z_{\mathrm{Last}}| \cdot e^{j\varphi_Z}} = \frac{|U|}{|Z_{\mathrm{Last}}|} \cdot e^{j(\varphi_U - \varphi_Z)} = |I| \cdot e^{j\varphi_I} \\[6pt] |I| = \frac{|U|}{|Z_{\mathrm{Last}}|} \\[4pt] \varphi_I = \varphi_U - \varphi_Z \\[4pt] \varphi = \varphi_U - \varphi_I = \varphi_U - (\varphi_U - \varphi_Z) = \varphi_Z \end{gathered} \]

Für die Berechnung des Laststroms teilen wir die Spannung durch die Lastimpedanz. Der Phasenwinkel des Stroms entspricht deshalb dem Phasenwinkel der Lastimpedanz multipliziert mit -1. Der Phasenwinkel φ wird aus Spannungswinkel minus Stromwinkel berechnet. Insgesamt entspricht der Phasenwinkel zwischen Spannung und Strom φ dem Phasenwinkel der Lastimpedanz φ_z. Betrachten wir in einem Beispiel die Phase der Impedanz einer Reihenschaltung aus R und L an der Sternspannung U₁. Die Zahlenwerte der Lastimpedanz sind willkürlich gewählt.

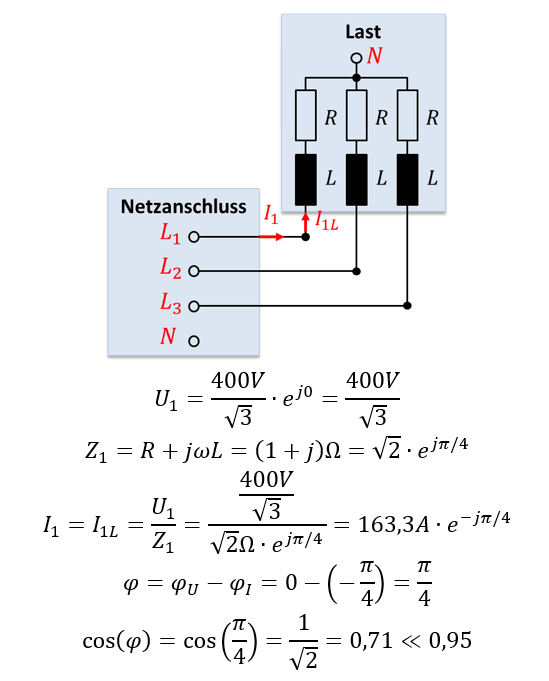
Last aus drei Strängen R und L in Sternschaltung am Netzanschluss L1, L2, L3, N

\[ \begin{gathered} U_1 = \frac{400\,\mathrm{V}}{\sqrt{3}} \cdot e^{j0} = \frac{400\,\mathrm{V}}{\sqrt{3}} \\[4pt] Z_1 = R + j\omega L = (1 + j)\,\Omega = \sqrt{2} \cdot e^{j\pi/4} \\[4pt] I_1 = I_{1L} = \frac{U_1}{Z_1} = \frac{\frac{400\,\mathrm{V}}{\sqrt{3}}}{\sqrt{2}\,\Omega \cdot e^{j\pi/4}} = 163{,}3\,\mathrm{A} \cdot e^{-j\pi/4} \\[4pt] \varphi = \varphi_U - \varphi_I = 0 - \left(-\frac{\pi}{4}\right) = \frac{\pi}{4} \\[4pt] \cos(\varphi) = \cos\left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}} = 0{,}71 \ll 0{,}95 \end{gathered} \]

Wichtig ist hier erstmal nur der Winkel. Der Phasenwinkel des Stroms entspricht dem der Impedanz mit anderem Vorzeichen. Sind R und ωL – wie im Beispiel – gleich groß, ist der cos(φ) viel zu klein. Das gibt Ärger mit dem Netzbetreiber.

Die Cosinus-Funktion ergibt für positive und für negative Winkel das gleiche Ergebnis. Es gilt cos(φ) = cos(-φ). Das ist ärgerlich, denn damit verschwindet bei der Angabe des cos(φ) das Vorzeichen des Winkels. Bei vorwiegend induktiver Last ist der Phasenwinkel positiv im Bereich φ_ind = [0 .. π/2]. Bei vorwiegend kapazitiver Last ist der Phasenwinkel negativ im Bereich φ_kap = [-π/2 .. 0].

Es gibt deshalb die zusätzlichen Angaben zum cos(φ):

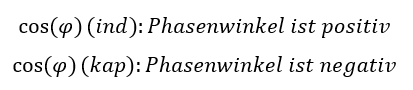
\[ \begin{gathered} \cos(\varphi) \text{ (ind): Phasenwinkel ist positiv} \\[4pt] \cos(\varphi) \text{ (kap): Phasenwinkel ist negativ} \end{gathered} \]

Weil elektrische Maschinen induktive Lasten darstellen, brauchen wir oft eine lokale Kompensation induktiver Blindleistung: Die Blindleistungskompensation.