Magnetische Felder werden mathematisch durch mehrere Größen beschrieben. Der elektrische Strom bewirkt zunächst eine magnetische Feldstärke H. Sie ist mit der elektrischen Feldstärke E vergleichbar. Es gilt die allgemeine Formel:
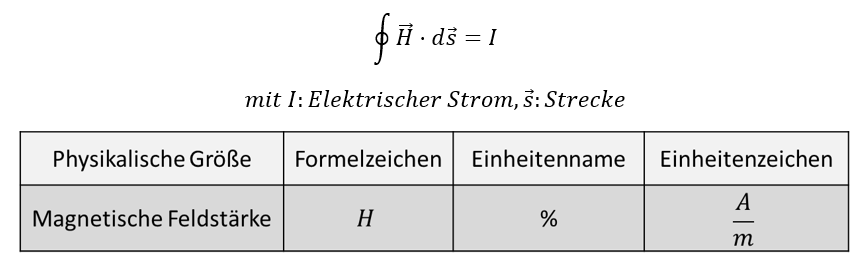
Das „Ringintegral“ H über der Strecke ds entspricht dem Strom, der das Feld verursacht. Das Ringintegral wird jeweils auf die Geometrien angewendet, in der sie den stromdurchflossenen Leiter für ihre Anwendung formen. Wenn der Draht gerade und lang ist, dann löst sich das Integral folgendermaßen in einer speziellen Formel in Wohlgefallen auf:
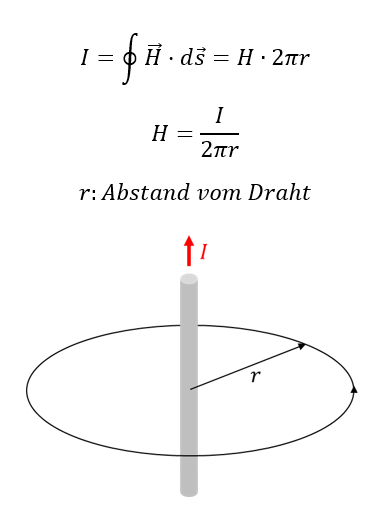
Die Intensität des H-Felds sinkt mit Abstand r zum Draht. Wichtig: Es handelt sich hier um eine spezielle Formel, die nur für lange gerade Drähte gilt. In anderen Geometrien gelten andere Formeln.
Erklärung des Ringintegrals
Das Ringintegral besagt anschaulich folgendes: Wir stellen uns gedanklich auf eine Feldlinie des H-Felds und laufen einmal entlang der Feldlinie im Kreis herum. Dabei addieren wir die Intensität des H-Felds auf dem Weg auf. Am Ende kommen wir wieder am Startpunkt an. Wir haben dabei einmal
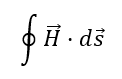
integriert. H entspricht immer der Intensität des Felds an dem Ort im Raum, an dem Sie gerade sind. Der Term ds beschreibt die Strecke, die sie zurückgelegt haben. Wenn Sie also eine kreisförmige Feldlinie entlanglaufen, dann laufen Sie dem Umfang des Kreises mit dem Radius r ab. Es gilt dann:
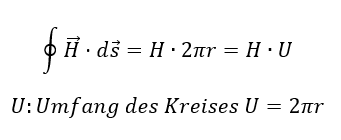
Die Intensität des H-Felds ist überall auf dem Kreisumfang U = 2πr gleich groß, weil hier überall der Abstand zum Leiter r gleich groß ist. Wenn Sie eine Feldlinie für die Integration wählen, die sehr nah am Draht verläuft, dann sind der Radius des Kreises und damit die Strecke ds klein. Bei festem Strom I ist dann das H-Feld groß. Bei einer weit entfernten Feldlinie mit gleichem Strom I im Draht sind Radius und Strecke ds größer. Dann muss das H-Feld kleiner sein. Auf diese Weise wird mathematisch beschrieben, wie das Feld mit steigendem Abstand zum Draht immer weniger intensiv wird.
Überlagerung mehrerer Ströme als Quellen
Die magnetischen Felder von n Strömen durch n Leiter überlagern sich. Um zu berechnen, wie hoch die magnetische Feldstärke an einem Ort im Raum ist, müssen zunächst die Abstände ri der Leiter von diesem Ort im Raum ermittelt werden. Dann brauchen wir noch die Intensitäten der Ströme. Wir berechnen nacheinander die Felder der einzelnen Leiter an diesem Ort und addieren die Teilergebnisse am Ende vektoriell. Das läuft wie in der Elektrostatik bei der Berechnung des elektrischen Felds mehrerer Punktladungen.
Es gibt einen einfacheren Weg für die Berechnung, deshalb gehe ich auf die Überlagerung nicht näher ein:
Verlaufen mehrere Ströme durch einen Integrationsweg des Ringintegrals, dann wirken sie alle im Ringintegral. Das Vorzeichen des Stroms hängt von der Stromrichtung ab. Mit Hilfe der „Rechte-Hand-Regel“ können Sie ermitteln, welcher Strom positiv wirkt. Wir lösen uns jetzt gedanklich von Feldlinien, die im Kreis um einen Leiter herum verlaufen. Diese sind mathematisch einfach, weil auf ihnen überall die gleiche Feldstärke H vorliegt. Sie können das Ringintegral auch auf beliebigen Integrationswege ds anwenden.
Im folgenden Beispiel gilt für die Integration entlang der schwarzen Linie:
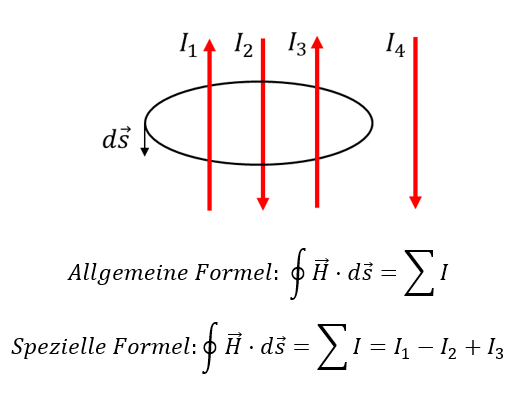
Diesen Zusammenhang nennt man „Durchflutungsgesetz“. Das Ringintegral entlang des schwarzen Kreises in der eingezeichneten Richtung ds umfasst nur die Ströme I1 bis I3. I4 liegt außerhalb des Integrationswegs und wirkt deshalb nicht im Ringintegral. I1 wirkt nach „Rechter-Hand-Regel“ positiv, weil die Finger in Richtung von ds zeigen, wenn der Daumen in Richtung I1 zeigt.
Diese Betrachtung ist zur Feldberechnung oft einfacher als die Anwendung der Überlagerung. Später werden wir den Integrationsweg des Ringintegrals fixieren. Die Intensität von H wird auf diesem Integrationsweg konstant sein. Dann gilt für eine Integration entlang der Länge l:
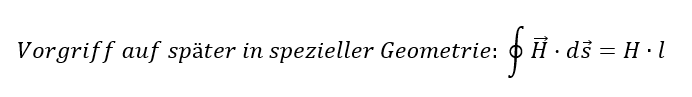
Achtung: Das ist keine allgemeine Formel, sondern das Ziel für eine vereinfachte Feldberechnung, die ohne Lösung des Ringintegrals auskommt.
Zusammenfassung
Ein elektrischer Strom bewirkt eine magnetische Feldstärke H. Sie wirkt ähnlich wie die elektrische Feldstärke E. Diese ist abhängig vom Abstand zur Feldquelle, also von Abstand zur stromführenden Leiter. Für die Berechnung der Intensität der magnetischen Feldstärke nutzen wir die Formel mit dem Ringintegral. Die Felder mehrerer Ströme überlagern sich. Deshalb nutzen wir folgende allgemeine Formel zur Feldberechnung:

Für elektrisch erzeuge Magnetfelder („Elektromagnet“) brauchen wir elektrischen Strom. Das Magnetfeld eines Permanentmagneten wird auf atomarer Ebene ebenfalls durch bewegte Ladung erzeugt. Das Erdmagnetfeld wird auch durch bewegte Ladung erzeugt. Der Effekt der Feldquelle ist also bei jedem Magnetfeld immer gleich.
Weiter