Regelungstechnik › Schwingende Systeme 2

Übertragungsfunktion

Im vorletzten Kapitel haben wir den Regelkreis aufgetrennt, um die Ringverstärkung zu ermitteln. Jetzt schließen wir den Regelkreis wieder und betrachten die Übertragungsfunktion eines Regelkreises. Wir können dafür die Ringverstärkung in die Formel der Übertragungsfunktion einsetzen. Betrachten wir dafür ein System aus zwei hintereinander geschalteten I-Blöcken in einem Regelkreis. Es sind zwei Speicher im Spiel, also ist eine Schwingung möglich. Es gilt:

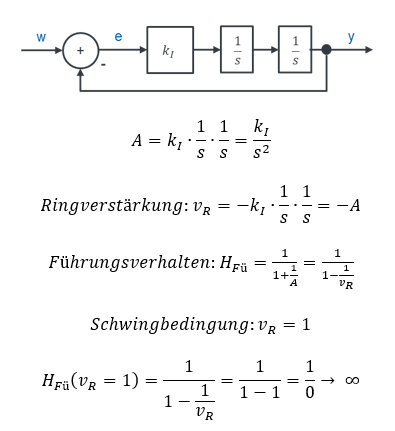
Regelkreis mit Regler k_I und zwei Integratoren 1/s

\[ \begin{gathered} A = k_I \cdot \frac{1}{s} \cdot \frac{1}{s} = \frac{k_I}{s^2} \\[6pt] \text{Ringverstärkung: } v_R = -k_I \cdot \frac{1}{s} \cdot \frac{1}{s} = -A \\[6pt] \text{Führungsverhalten: } H_{\mathrm{FÜ}} = \frac{1}{1 + \frac{1}{A}} = \frac{1}{1 - \frac{1}{v_R}} \\[6pt] \text{Schwingbedingung: } v_R = 1 \\[6pt] H_{\mathrm{FÜ}}(v_R = 1) = \frac{1}{1 - \frac{1}{v_R}} = \frac{1}{1 - 1} = \frac{1}{0} \rightarrow \infty \end{gathered} \]

Wenn ein geregeltes System schwingt, geht der Nenner seiner Übertragungsfunktion gegen 0. Damit wird die Übertragungsfunktion selbst unendlich groß. Wir können ausrechnen, wann ein System schwingt. Dafür setzen wir den Nenner seiner Übertragungsfunktion zu 0 und schauen, ob es für die Gleichung eine Lösung gibt. Falls ja, schwingt das System.

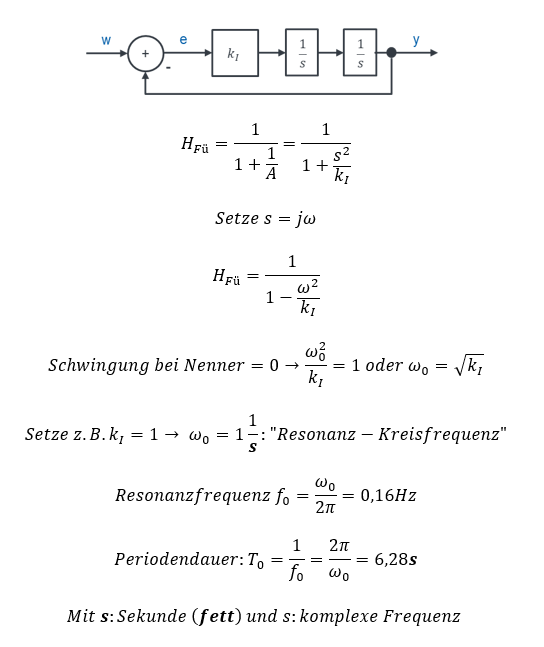
\[ \begin{gathered} H_{\mathrm{FÜ}} = \frac{1}{1 + \frac{1}{A}} = \frac{1}{1 + \frac{s^2}{k_I}} \\[6pt] \text{Setze } s = j\omega \\[6pt] H_{\mathrm{FÜ}} = \frac{1}{1 - \frac{\omega^2}{k_I}} \\[6pt] \text{Schwingung bei Nenner} = 0 \rightarrow \frac{\omega_0^2}{k_I} = 1 \text{ oder } \omega_0 = \sqrt{k_I} \\[6pt] \text{Setze z. B. } k_I = 1 \rightarrow \omega_0 = 1\,\frac{1}{\mathrm{s}}\text{: „Resonanz-Kreisfrequenz“} \\[6pt] \text{Resonanzfrequenz } f_0 = \frac{\omega_0}{2\pi} = 0{,}16\,\mathrm{Hz} \\[6pt] \text{Periodendauer: } T_0 = \frac{1}{f_0} = \frac{2\pi}{\omega_0} = 6{,}28\,\mathrm{s} \\[6pt] \text{Mit } \mathrm{s}\text{: Sekunde (aufrecht) und } s\text{: komplexe Frequenz (kursiv)} \end{gathered} \]

Hinweis: Hier macht die Angaben von Zeiten in Minuten keinen Sinn, deshalb sind ausnahmsweise Sekunden verwendet worden. Für Sekunden wird der Buchstabe s fett dargestellt.

Es gibt eine Lösung, bei der der Nenner der Übertragungsfunktion 0 wird. Also schwingt das System bei der Kreisfrequenz, bei der der Nenner 0 wird. Das ist unsere Resonanzfrequenz.

Die Sprungantwort eines schwingenden Systems schwingt im Anschluss an den Eingangssprung. Der Zeitverlauf der Sprungantwort des Beispielsystems mit k_I = 1 ist in der unteren Abbildung dargestellt. Der Sprung der Eingangsgröße in blau erfolgt bei t = 1s.

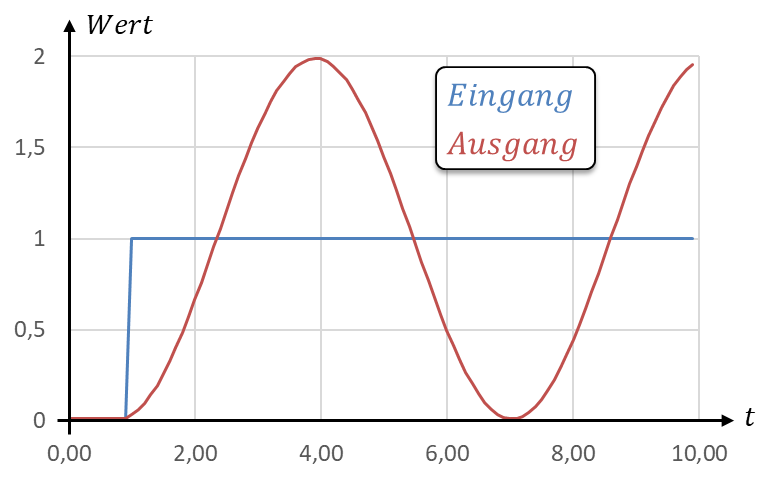
Sprung am Eingang bei t = 1 und ungedämpfte Schwingung des Ausgangs zwischen 0 und 2

Die Schwingung der Ausgangsgröße startet, sobald der Eingang springt. Die Periodendauer T₀ in der Grafik entspricht dem berechneten Wert von T₀ = 6,28s. Sie kann aus dem Abstand der Maxima bestimmt werden. Eine sinusförmige Dauer-Schwingung wird über den Parameter „Schwingfrequenz“ oder „Resonanzfrequenz“ charakterisiert. Dieser Parameter liegt immer als Kreisfrequenz ω, als Frequenz f und als Periodendauer T vor.

Der Spitzenwert der Schwingung beträgt 1. Die Ausgangsgröße schwingt nach dem Sprung um die Führungsgröße w = 1 herum.

Aufgabe

Modellieren Sie das geregelte System in Matlab Simulink. Regen Sie das System mit einem Sprung von 0 auf 1 an. Variieren Sie k_I und beobachten Sie, wie sich das Ausgangsverhalten ändert. Hier die Lösung für k_I = 1:

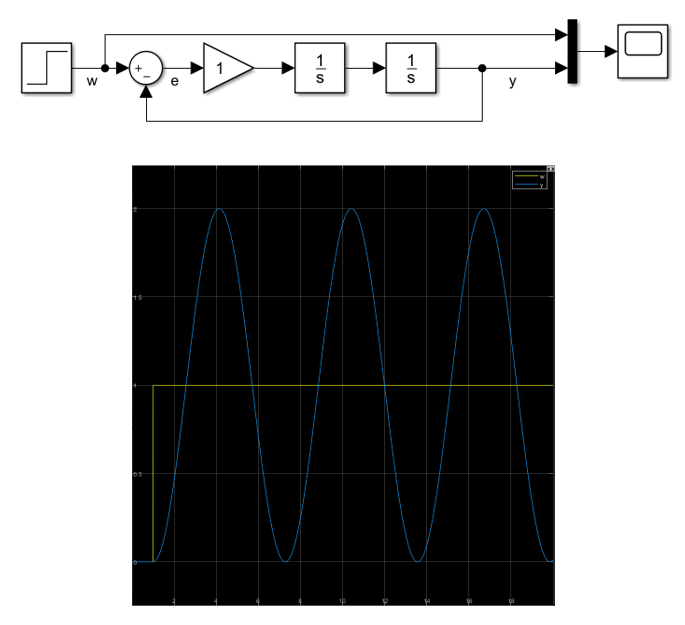
Simulationsmodell des Regelkreises mit Sprungquelle, Verstärkung 1, zwei Integratoren und Oszilloskop sowie simulierte Dauerschwingung

Die Resonanzfrequenz ist abhängig von K_I. Also erwarten wir, dass sie sich mit Variation von K_I ändert. Der Parameter K_I ist in diesem Regelkreis wie die Fadenlänge beim Pendel: Er beeinflusst die Resonanzfrequenz.