Am Beispiel des realen Widerstands zeige ich Ihnen Eigenschaften, die viele weitere Bauelemente ebenfalls aufweisen. In diesem Kapitel gehe ich dazu mehr ins Detail, in den Kapiteln zu den anderen Bauelementen nicht mehr.
Legen wir 10 Widerstände mit R=10kΩ nebeneinanderlegen und vermessen deren Widerstandswert nacheinander mit einem Multimeter. Dann stellen wir fest, dass die Werte der Widerstände sich unterscheiden, obwohl der Hersteller sie alle mit der gleichen Bezeichnung verkauft. Es ist weder möglich, unterschiedliche Dinge gleicher Bauart exakt identisch herzustellen, noch dass diese gleichbleiben. Sie müssen nur genau genug messen um überall Unterschiede festzustellen.
Initiale Genauigkeit
Bauelemente sind in Genauigkeitsklassen eingeteilt. Wenn Sie 10kΩ-Widerstände der 1%-Klasse kaufen, dann liegen die Werte um ±1% um den Sollwert von 10kΩ zwischen 9,99 kΩ und 10,1 kΩ. Es gibt auch Widerstände mit 0,1% Abweichung vom Sollwert und noch bessere. Je genauer der Widerstandswert, desto teurer der Widerstand.
>br>
Die Verteilung der Werte folgt der Gauß-Verteilung aus der Stochastik. Dabei werden auf der Y-Achse die Anzahl der Widerstände und auf der X-Achse die Werte dargestellt. Wir betrachten dabei sehr viele Widerstände, die nominell den gleichen Wert haben sollten. Je mehr dieser Widerstände einen bestimmten Wert haben, desto größer ist der Wert auf der Y-Achse. Es wird deutlich, dass die meisten Werte in der Nähe des Sollwerts liegen und nur extrem wenige an den Bereichsgrenzen liegen. Siehe dazu hier.
Sie können sicher sein, dass der Wert eines Widerstands innerhalb des spezifizierten Bereichs (z. B: ±1% des Sollwerts) liegt. Wenn Sie den Wert eines Widerstands genauer wissen möchten, dann müssen Sie mit einem Multimeter seinen Wert nachmessen. Beachten Sie beim Messen, dass es auch unterschiedlich genaue Multimeter gibt, die sind auch nicht ideal ;-).
Alterung
Wenn Sie den Wert eines Widerstands ausreichend genau kennen, können Sie noch nicht sicher sein, dass er diesen Wert behält. Mit zunehmendem Alter ändert sich der Wert eines Widerstands. Diese Änderungsrate wird üblicherweise in PPM/Jahr angegeben. PPM steht für Parts per Million. Die Angabe 10 PPM/Jahr bedeutet, dass sich der Wert pro Jahr um 10 Millionenstel des Sollwerts ändert. Sie berechnen die Widerstandsänderung ΔR eines Widerstand mit der Formel

Nach 10 Jahren im Einsatz weicht der Widerstandswert vom Nominalwert um maximal ±0,01% ab. Ein Widerstand mit dem Nominalwert R = 10 kΩ ändert also seinen Wert um bis zu ±1Ω. Oft können wir diesen Effekt ignorieren, weil er so klein verglichen mit anderen Problemen ist.
Bauelemente altern nicht nur dadurch, dass Zeit vergeht. Sie altern schneller, wenn sich ihre Temperatur zyklisch ändert. Je öfter und je intensiver die Temperaturänderung stattfindet, desto schneller altern sie. Dadurch ändert sich ständig ihre Ausdehnung. Das führt zu Kräften an Übergängen zwischen Materialien mit unterschiedlichen thermischen Ausdehnungskoeffizienten.
Temperaturabhängigkeit
Widerstände (und alle anderen Bauelemente) sind temperaturabhängig. Der Widerstandswert ist abhängig von der Temperatur im Inneren des Bauelements. In Datenblättern wird dazu die Änderung des Widerstandswerts pro °C angegeben. Ein Widerstand mit einem Temperaturkoeffizienten α ändert seinen Wert nach der folgenden allgemeinen Formel über der Temperatur.

Wird unser 10kΩ-Widerstand z. B. im Auto eingesetzt, muss er Temperaturen zwischen -40°C und 85°C aushalten können. Die Nominaltemperatur, für die er ausgelegt ist, beträgt 25°C. Es treten also im normalen Betrieb Änderungen von +60°C und -65°C auf. Für das Beispiel nutzen wir einen (sehr schlechten) Temperaturkoeffizienten α = 0,1%/°C. Das führt zu einer zusätzlichen Widerstandsänderung bei extrem kalten Temperaturen von
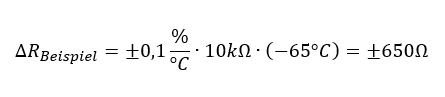
Diesen Effekt müssen wir bei der Auslegung von Schaltungen beachten. Es gibt natürlich für mehr Geld auch Widerstände mit kleinerem Temperaturkoeffizienten am Markt.
Maximale Leistung
Elektrische Leistung erwärmt einen Widerstand. Diese Wärme muss er an seine Umgebung abgeben, sonst steigt seine Temperatur immer weiter an. Ab einer Grenztemperatur verbrennt der Widerstand und er wird zerstört. Widerstände werden in unterschiedlichen Leistungsklassen angeboten. Je größer (im Sinne der Geometrie, nicht im Sinne des Widerstandswerts) er ist, desto mehr Oberfläche hat er und desto mehr Wärme gibt er an die Umgebung ab. Damit ist er für höherer Leistung ausgelegt.
Elektrisches Ersatzschaltbild (ESB)
Ein realer Widerstand in der Bauform bedrahteter Widerstand besteht aus zwei Zuleitungsdrähten und dazwischen dem Widerstandsmaterial. Die Zuleitungsdrähte werden zum Befestigen (Anlöten) an der Schaltung genutzt.
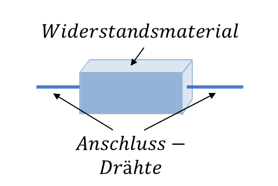
So ein Draht mit der Länge einiger cm wirkt als Spule mit der Windungszahl n = 1. Er verhält sich also nicht nur wie ein Widerstand, er hat auch induktive Eigenschaften. Die Induktivität eines solchen Drahts ist sehr gering und liegt im nH oder µH-Bereich. Die komplexe Impedanz dieser parasitären Induktivität lautet
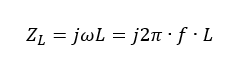
Wenn in der Schaltung Signale mit extrem hoher Frequenz f auftreten, dann ist die Impedanz trotz des kleinen L-Werts nicht mehr klein. Ein Stück Draht mit der Induktivität L = 10nH wirkt bei der Frequenz f = 100MHz mit der Impedanz
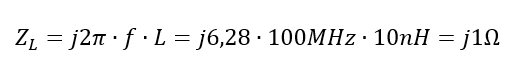
Wenn der Widerstand selbst sehr hochohmig ist, dann spielt das keine Rolle. Beträgt der nominale Wert des Widerstands aber nur R = 1Ω, dann ändert sich sein Verhalten durch die parasitäre Spule für das Signal mit sehr hoher Frequenz enorm.
Betrachten wir deshalb Widerständen in SMD (Surface Mounted Devices) Bauform. Diese werden heute vorwiegend in Schaltungen eingesetzt. Ein SMD-Widerstand besteht aus zwei Metallkappen mit dem Widerstandsmaterial dazwischen.
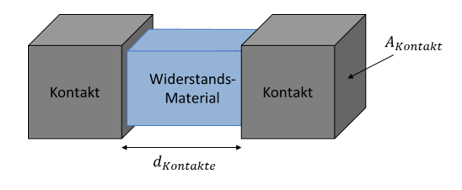
Die beiden Anschluss-Kappen bilden miteinander einen parasitären Kondensator. Zwischen den Anschlüssen ist schlecht leitendes Material (zumindest bei hochohmigen Widerständen). Sie haben zueinander den Abstand d. Die Fläche A des Kondensators ist über die Querschnittsfläche des Widerstandsmaterials gegeben. Das Widerstandsmaterial wird oft so gewählt, dass es nur wenig εr aufweist. Für den parasitären Kondensator gilt:

Bei diesem Aufbau ist kein Zuleitungsdraht vorhanden. Deshalb ist die Zuleitungsinduktivität deutlich geringer als bei bedrahteten Widerständen. Durch den Aufbau des Bauelements können wir also auf die parasitären Eigenschaften Einfluss nehmen. Für den Parasitären Kondensator gilt:

Oft ist die parasitäre Kapazität C verschwindend gering, weil der Abstand d so groß ist. Die Impedanz des Kondensators ist dann sehr hoch verglichen mit der Impedanz der anderen Elemente des ESBs. Signale mit sehr hohen Frequenzen reduzieren die Impedanz des Kondensators, denn die Frequenz Omega steht im Nenner der Kondensatorimpedanz. Der gleiche Kondensator wirkt bei Signalen mit niedriger Frequenz hochohmig und bei Signalen mit hoher Frequenz niederohmig.
Elektrisches Ersatzschaltbild ESB
Das Ersatzschaltbild des realen Widerstands besteht aus einem idealen Widerstand, der parasitären Spule und dem parasitären Kondensator.
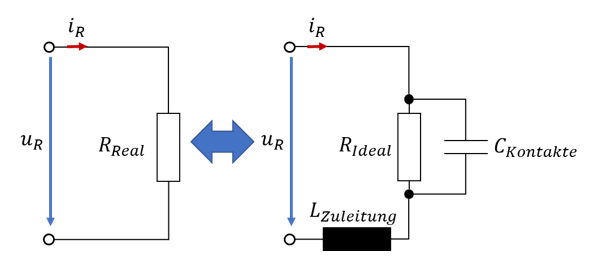
Strom und Spannung am realen Widerstand (links) verhalten sich so, wie Strom und Spannung am Ersatzschaltbild (rechts). Damit bildet das Ersatzschaltbild das Verhalten des realen Widerstands elektrotechnisch ab. Sie können in Gedanken jeden realen Widerstand in einem Schaltplan durch das Ersatzschaltbild ersetzen.
Der Kondensator wirkt parallel zum Widerstand. Die Impedanz des Kondensators ist bei niedriger Frequenz der Signale sehr hoch. Ein hochohmiges Bauelement in einer Parallelschaltung hat fast keine Wirkung auf die Schaltung, weil durch das Bauteil nur ein Bruchteil des Stroms fließt. Der Strom der Signale mit sehr hoher Frequenz fließt fast ausschließlich über den Kondensator und überbrückt damit den Widerstand. Ein parallel geschalteter parasitärer Kondensator schließt hochfrequente Signale kurz.
Die parasitäre Spule ist in Reihe zum Widerstand geschaltet. Bei niedriger Frequenz im Signal ist die Impedanz der Spule gering. In der Reihenschaltung wirkt eine niedrige Impedanz kaum. Die Impedanz der Spule steigt mit der Frequenz der Signale an. Damit fließt bei hoher Frequenz weniger Strom pro angelegter Spannung in die Schaltung hinein.
Die Wirkung von Spule und Kondensator bemerken Sie am realen Widerstand erst bei hohen Signalfrequenzen. Deshalb müssen Sie die im ESB enthaltenen parasitären Bauelemente oft erst bei hohen Frequenzen berücksichtigen. Je nachdem wie groß L und C der parasitären Bauelemente sind, wirkt bei hohen Frequenzen vorwiegend die Spule oder der Kondensator.
Die Detailtiefe des Ersatzschaltbilds (ESB) wählen sie selbst. Es gibt noch weitere Effekte, die aber klein gegenüber den hier beschriebenen Effekten sind. Je nachdem was Sie mit dem Ersatzschaltbild erreichen wollen entscheiden Sie, welche der bekannten Effekte Sie berücksichtigen und welche nicht. Sie finden zu allen elektrischen Bauelementen und zu vielen anderen elektrischen Komponenten die elektrischen Ersatzschaltbilder in unterschiedlicher Detailtiefe im Internet.
Kurzzusammenfassung ESB
Allgemein gilt: Der Widerstandswert ist material- und geometrieabhängig. Parasitäre Bauelemente wie Kondensatoren, Spulen und parasitäre weitere Widerstände sind ebenfalls material- und geometrieabhängig. Deshalb steigen oder sinken deren Einfluss über Geometrie und Material. Dazu kommen Einflüsse aus der Verbindung des Bauelements mit einer Schaltung.
Schauen Sie sich bei Interesse den sehr guten
Wikipedia-Artikel zum Ohm´schen Widerstand an. Hier finden Sie u. A. noch die Spannungsabhängigkeit und die Frequenzabhängigkeit des Widerstandswerts.
Weiter