Zwei Bauelemente sind parallelgeschaltet, wenn zwischen den Anschlüssen, die die Bauelemente verbinden, keine anderen Bauelemente liegen. Wenn man sich gedanklich auf den einen Anschluss eines Bauelements setzt, kann man in der Schaltung nur über Leitungen zu einem Anschluss des anderen Bauelements kommen. Wenn dies für beide Anschlüsse beider Bauelemente gilt, dann sind diese parallelgeschaltet.
Sie können mit diesem Merkmal in einer Schaltung prüfen, ob eine Parallelschaltung vorliegt. In einer Parallelschaltung fällt an beiden Bauelementen nach der Maschenregel die gleiche Spannung ab: Es gilt
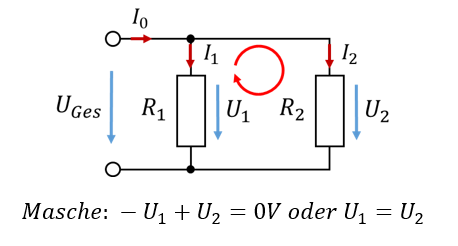
Der Strom teilt sich bei einer Parallelschaltung nach der Knotenregel auf. Es können mehr als zwei Bauelemente parallelgeschaltet sein.

In der Beispielschaltung kann geprüft werden, welche Bauelemente parallelgeschaltet sind. Setzen Sie sich dafür gedanklich auf den oberen Anschluss von Widerstand R3. Sie kommen nur über Leitungen zum oberen Anschluss von R4. Setzen Sie sich anschließend auf den unteren Anschluss von R3. Sie gelangen ebenfalls nur über Leitungen – also ohne dass ein anderes Bauelement im Weg liegt – zum unteren Anschluss von R4. Diese Bauelemente sind also parallelgeschaltet.
Wenn Sie den gleichen Test mit R2 und R3 durchführen werden Sie feststellen, dass diese vom oberen Anschluss von R3 aus gesehen direkt miteinander verbunden sind. Vom unteren Anschluss von R3 aus gesehen liegen aber die Spannungsquelle und R1 im Weg. Deshalb sind R2 und R3 nicht parallelgeschaltet.
Wird die gleiche Schaltung etwas anders gezeichnet, fällt die Analyse etwas schwerer. Der untere Schaltplan entspricht von seinen Verbindungen und seiner Funktion her exakt dem oberen, die Anordnung der Widerstände und der Quelle ist aber ungeschickter gewählt. In dieser Schaltung wirkt es auf den ersten Blick so, als seinen R1 und R2 parallelgeschaltet, während man die Parallelschaltung von R3 und R4 nicht mehr auf den ersten Blick als solche erkennt.
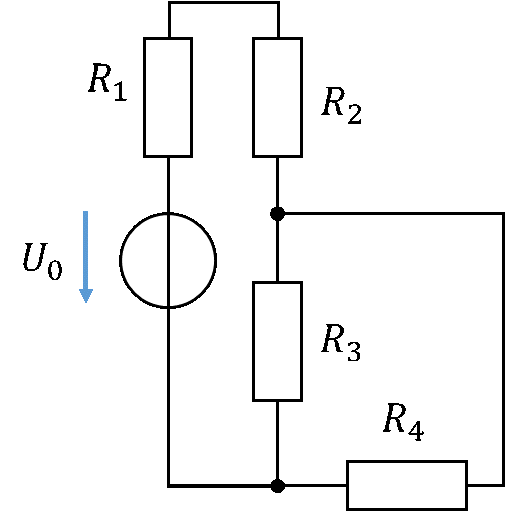
Achten Sie darauf, dass nicht alle Bauelemente parallelgeschaltet sind, die parallel zueinander gezeichnet sind und nicht alle Bauelemente in Reihe geschaltet sind, die übereinander oder nebeneinander gezeichnet sind.
Auch in einer Parallelschaltung würde es die Berechnung vereinfachen, wenn beide Widerstände zu einem zusammengefasst werden könnten, der das gleiche Verhalten zeigt wie die Parallelschaltung aus zwei Widerständen. Auch hier gilt: Das Verhalten des Ersatzwiderstands ist gleich der Parallelschaltung der Widerstände, wenn Spannung und Strom an beiden Schaltungen gleich groß sind.
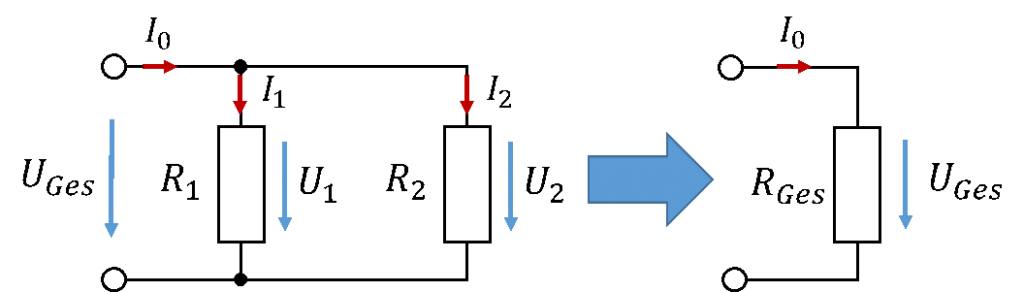
Der Strom durch den Ersatzwiderstand RGes muss gleich der Summe der Teilströme durch R1 und R2 sein. Es gilt:
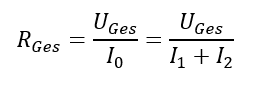
Weil bei der Parallelschaltung von Widerständen eine Summe im Nenner steht, kann der Bruch mathematisch nicht so einfach umgeformt werden wie bei der Reihenschaltung. Die Gleichung ist für Leitwerte statt Widerstände einfacher zu lösen:
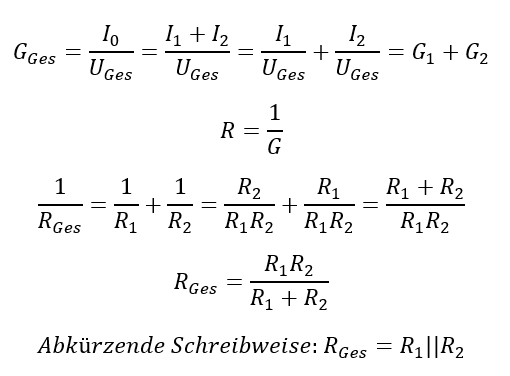
Die abkürzende Schreibweise mit den beiden senkrechten parallelen Strichen ist nur zur Reduktion von Schreibaufwand gedacht. Damit kennzeichnen Sie in einer Rechnung, dass zwei Bauelemente parallelgeschaltet sind. Gemeint ist damit immer die mathematisch korrekte Schreibweise direkt darüber. Beispiel:
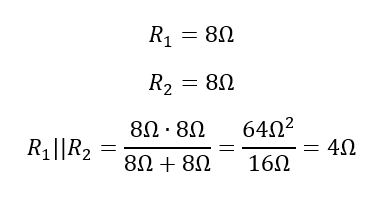
In Parallelschaltung gilt grundsätzlich: Der Ersatzwiderstand ist kleiner als die Original-Widerstände. In Reihenschaltung ist das umgekehrt.
Für die Spannungen zweier parallelgeschalteter Bauelemente gilt:
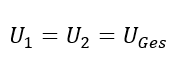
Für die Berechnung des Ersatzwiderstands wird also die gleiche Spannung im Zähler, aber ein größerer Strom im Nenner genutzt. Deshalb muss der Ersatzwiderstand immer kleiner als die Teilwiderstände sein.
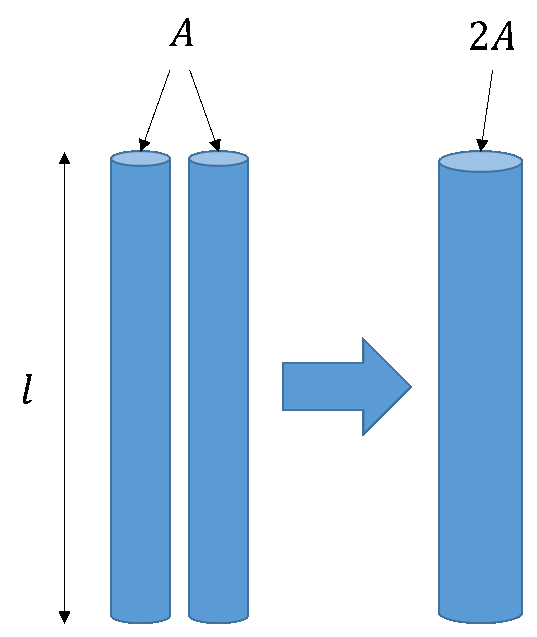
Die Parallelschaltung von Widerständen kann am Wassermodell mit zwei Rohren erklärt werden, die nebeneinander verlaufen. Die Höhendifferenz der Rohre ist gleich, so wie die Spannung an zwei parallelen Widerstände gleich groß ist. Nehmen wir zur Vereinfachung an, dass beide Rohre gleichen Durchmesser, gleiche Länge und gleichen Materialparameter aufweisen. Wenn wir versuchen, beide Rohre durch ein einziges Ersatz-Rohr mit gleichen Eigenschaften zu beschreiben, stellen wir fest: Die Fläche A des Ersatzrohres muss verdoppelt werden.
Für den Widerstand eines einzelnen Rohrs gilt
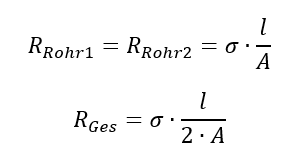
Der effektiv wirksame Widerstandswert – also die Behinderung des Wasserflusses, der aufgrund einer Höhendifferenz durch Rohre fließt – hat sich durch die Parallelschaltung halbiert.
Das Beispielnetzwerk aus dem vorherigen Kapitel, in dem bereits die in Reihe liegenden Widerstände zusammengefasst worden sind, kann weiter vereinfacht werden. Alle vier Ersatzwiderstände sind parallelgeschaltet.
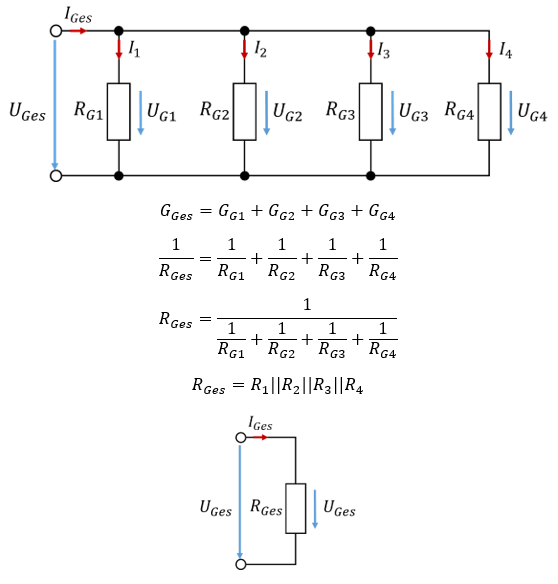
Die Schaltung kann nochmal stark vereinfacht werden. Die untere Schaltung verhält sich hinsichtlich Spannung und Strom genau wie die obere Schaltung, wenn der Gesamtwiderstand nach den Regeln der Parallelschaltung berechnet wird.
Am Widerstand können Spannung und Strom der Gesamtschaltung einfach mit dem Ohm´schen Gesetz in einer Gleichung berechnet werden. Das ist eine heftige Vereinfachung der Komplexität. Jede Schaltung, die aus linearen Bauelementen besteht, kann auf diese Weise vereinfacht werden.
Es gibt eine Online-Simulation zu vielen Elektrotechnik-Themen, die sehr gut veranschaulicht, wie Spannung und Strom sich verhalten. Die Parallelschaltung von zwei Widerständen ist dort sehr schön simuliert. Schauen Sie bitte mal bei Falstad (https://www.falstad.com/circuit/) und stellen Sie folgendes ein:
Schaltungen/Grundlagen/Ohm´sches Gesetz, Kirchhoff´sches Gesetz 1
Sie sehen in der Simulation die Intensität der Spannung als Farbe. An der Quelle oben die 5V in grün, unten an der Masse die 0V in grau. Die Intensität des Stroms wird als Teilchenbewegung angezeigt. Sie erkennen, dass durch den niederohmigen Widerstand mehr Strom fließt als durch den hochohmigen. Sie können die Werte der Quelle und der Widerstände einstellen und beobachten, wo wie viel Strom entlang fließt.
Im Beispiel „Gemischte Widerstandsschaltungen“ direkt darunter im Auswahlmenü finden Sie eine Möglichkeit, Reihenschaltungen zu simulieren. Sie können mit Schaltern Reihen- und Parallelschaltungen erstellen und beobachten. Ich halte viel von dem Tool, weil es Elektrotechnik grafisch und ohne Zahlen erklärt. Sie finden zu vielen anderen Themen dieses Tutorials unter Falstad anschauliche Beispiele.
Analogie zwischen Spannung, Potential und Höhen
Potentiale und Spannungen in Maschen können mit Höhen von Zimmern in einem Haus verglichen werden. Betrachten wir in der folgenden Abbildung rechts eine elektrische Schaltung als Beispiel mit vorgegebenen Spannungen und Potentialen. Die Potentiale sind in rot und die Spannungen in blau abgebildet. Die Spannung der Quelle U0=5V teilt sich an 5 Widerständen in Teilspannungen auf.
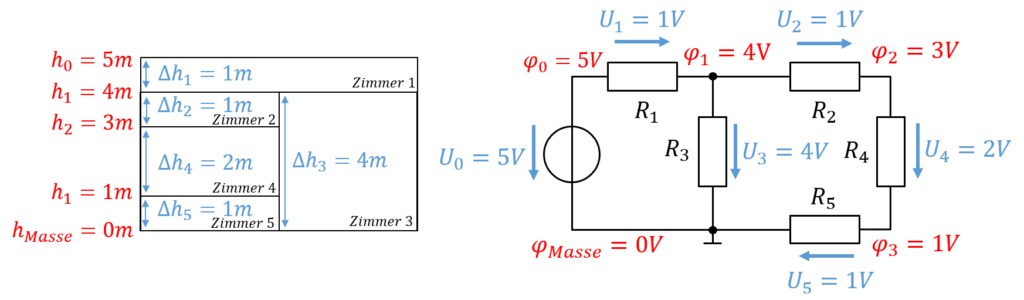
Links ist ein Haus mit unterschiedlich hohen Zimmern dargestellt. Die Zimmer entsprechen den Widerständen. Das Haus ist insgesamt 5m hoch. Die Gesamthöht des Hauses teilt sich in Teilhöhen der Zimmer auf. Die absoluten Höhen der Zimmerdecken entsprechen den Werten der Potentiale in der Schaltung. Die Höhendifferenzen entsprechen den Spannungen.
Zimmer 1 benötigt die oberste Etage komplett. Zimmer 3 ist so hoch wie Zimmer 2, 4 und 5 zusammen. Diese Zimmer liegen übereinander bzw. nebeneinander. Eine Reihenschaltung entspricht dem Stapeln von Zimmern übereinander. Eine Parallelschaltung der Anordnung von Zimmern nebeneinander.
Die Maschengleichung der rechten Masche U3=U2+U4+U5 kann auf die Höhendifferenzen übertragen werden. Die Höhendifferenz von Zimmer 3 entspricht offensichtlich der Summe der Höhendifferenzen der Zimmer 2, 4 und 5.