Die Sinus-Funktion wird zur Berechnung von Längen und Winkeln an einem Dreieck eingesetzt. Betrachten wir ein Dreieck mit den Seitenlängen a, b und c und dem Winkel φ:
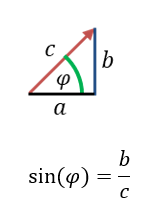
Die Sinus-Funktion gibt an einem Dreieck die Länge der Seite b in Relation zur Länge von Seite c an. Wir setzen dieses Dreieck in einen Kreis in einem x-y-Koordinatensystem ein:
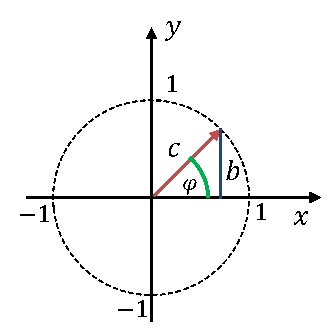
Wir bewegen den roten Zeiger gedanklich entlang der gestrichelten schwarzen Linie in der oberen Abbildung. Dadurch ändern wir den Winkel φ, wir lassen die Länge c des roten Zeigers aber konstant. Wenn der gestrichelte Kreis die Achsen immer an den Punkten 1 und -1 schneidet, dann gilt immer c = 1. Der Zusammenhang zwischen b und c vereinfacht sich mit c = 1 zu:
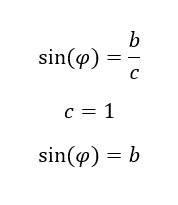
Das gilt auf allen Punkten des gestrichelten Kreises. Das Ergebnis der Sinus-Funktion kann an diesem Kreis grafisch veranschaulicht werden. Wenn der Winkel φ verändert wird, können wir an der Länge der blauen Linie b direkt ablesen, wie hoch der Wert von sin(φ) ist. Der Sinus eines Winkels kann anhand der Länge einer Linie abgelesen werden. Das ist eine gute Vereinfachung.
Wem das zu schnell geht, dem empfehle ich folgendes Video zu den Grundlagen von Sinus und Cosinus:
Als nächstes vergrößern wir den Winkel φ kontinuierlich über der Zeit. Damit wandert der rote Zeiger gegen den Uhrzeigersinn um den Kreis herum. Es gilt:
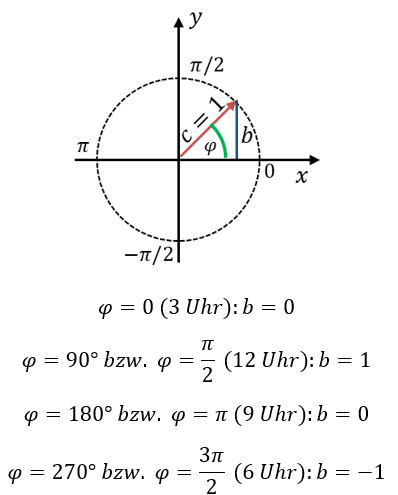
Der Winkel φ ändert sich über der Zeit t, und damit ändert sich auch die Länge b.
Die Zeit eines vollständigen Kreisumlaufs definieren wir als Periodendauer T. T beschreibt also die Zeitspanne bis zur ersten Wiederholung des Verlaufs. Bei φ = 2π gilt t = T. Die Zeit t entspricht dann einer Periodendauer T. Jetzt können wir den Verlauf von b auf eine Zeitachse übertragen und erhalten folgende Grafik für b(t):
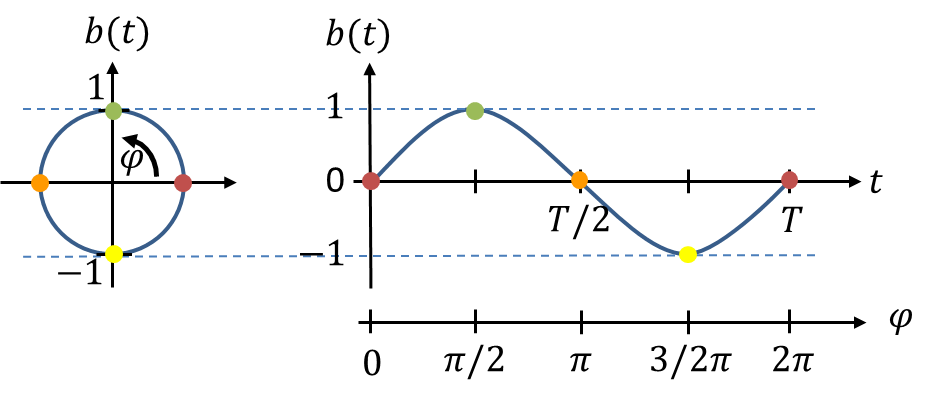
Die farblichen Punkte auf dem Kreis entsprechen denen im rechten Zeitverlauf. Die y-Werte, also die Werte von b(t), stimmen links und rechts überein. Es ist eine vollständige Kreisumdrehung – also eine Periode – dargestellt. Der Winkel φ hat einen Wertebereich von φ = [0.. 2π].
Der Verlauf b(t) = sin(φ) weist noch keine Zeitabhängigkeit auf. Wenn sich der Winkel über der Zeit ändert, brauchen wir eine Formel für dessen Zeitabhängigkeit. Es gilt:
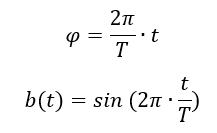
Um zu prüfen, ob diese Formel den Verlauf in der rechten Abbildung richtig wiedergibt, setzen wir zur Probe ein paar Werte für t ein. Die Zeit t ändert sich über eine Kreisumdrehung im Wertebereich t = [0 .. T].
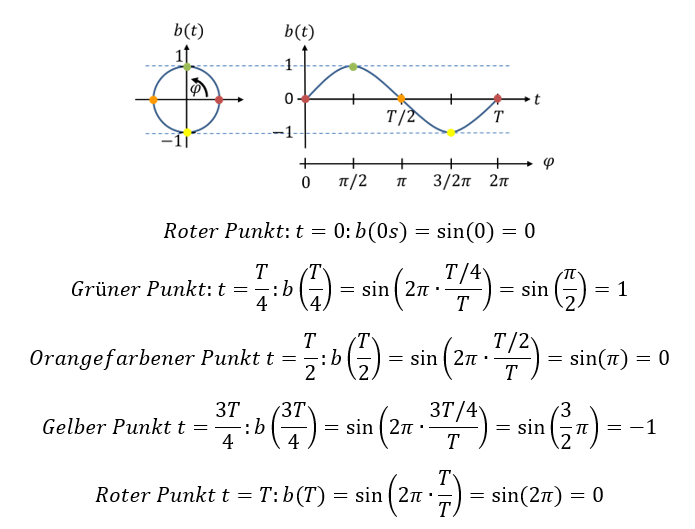
Durch Einsetzen von Zahlenwerten in eine Formel haben wir gezeigt, dass diese Formel gültig ist. Die Zahlenwerte entsprechen alle den erwarteten Werten, die wir in der Grafik des Kreises sehen.
Wir können auch Werte von t außerhalb der Periode T in die Formel einsetzen. Dann drehen wir den Punkt am Kreis einmal rum und dann noch weiter. Jede vollständige Drehung können wir auch weglassen, ohne das Ergebnis zu verändern. Es gilt z. B. sin(3π) = sin(π). Eine vollständige Umdrehung weist den Winkel 2π auf. Die Drehung um 3π dreht also einmal in Kreis und dann nochmal um π weiter.
Wir haben damit eine Formel gefunden, mit der ständig weiterdrehende Größen an einem Kreis mathematisch beschreiben können. Das sind sinusförmige Größen der allgemeinen Form
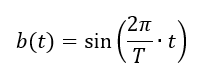
Der Parameter t in der Gleichung stellt die Zeit dar. Er ist wie das x in Gleichungen mit f(x) in der Schulmathematik. Wenn Sie b zu einer bestimmten Zeit berechnen wollen, dann setzen Sie diese Zeit t in die Gleichung ein. Die Formel hat dann eine einzige Lösung b als Zahl. Das wollen wir aber gar nicht erreichen. Die Formel selbst ist die Lösung des Problems: Die mathematische Beschreibung einer Wechselgröße über der Zeit t. Sie setzen also normalerweise nicht für t einen Zeitwert ein, sondern Sie nutzen diese Formel für weitere Berechnungen.
Das ist wie mit z. B. einer Geradengleichung y = m ∙ x + b. Die Gleichung beschreibt alle Punkte y auf der Geraden mathematisch. Sie können durch Einsetzen von x einen Wert y berechnen. Das ist nett, aber oft nicht das Ziel. Sie können die Gleichung auch nutzen um zu prüfen, ob eine andere Gerade parallel zu ihr verläuft oder diese schneidet. Dafür brauchen Sie die Gleichung an sich, nicht einen einzigen Zahlenwert. In der Elektrotechnik nutzen wir die obere Gleichung für weitere Berechnungen.
Weiter