Der Ladungszustand an einem Ort wird mit dem Begriff elektrisches Potential φ beschrieben. Je mehr Elektronenüberschuss in einem Körper vorhanden ist, desto stärker negativ ist sein Potential. Bei Elektronenmangel ist das Potential eines Körpers positiv. Das Potential ist mit der Ladung der Körper und dem Abstand der Körper voneinander verknüpft. In der Elektrostatik wird dieser Zusammenhang genauer definiert, darauf wird hier verzichtet. Für die Anschauung genügt es, dass Sie Potential und Ladung als ähnliche oder verwandte Größen betrachten.

Die elektrische Spannung U ist als Differenz zweier Potentiale definiert. Zwischen den beiden Körpern kann eine Spannung
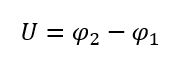
gemessen werden. Der Wert der Spannung ist positiv, wenn der Spannungspfeil vom höheren zum niedrigeren Potential weist. Eine Spannung wird auch zwischen zwei positiv geladenen Körpern gemessen, wenn einer der beiden mehr positiv geladen ist als der andere. Eine Spannung zeigt also eine Ladungsdifferenz an.
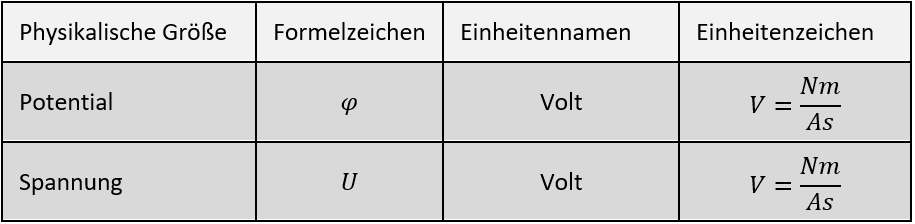
Die Einheit der Spannung ist Volt. Dann muss auch die Einheit des Potentials Volt sein, denn links und rechts einer Gleichung muss immer die gleiche Einheit stehen. Das Volt kennen Sie wahrscheinlich schon.
Spannungen sind aus dem Alltag bekannt. An einer Steckdose liegt eine Spannung von U=230V an. Eine LiPo-Batterie, die z. B. im Smartphone verbaut ist, weist eine Spannung von U=3,7V auf. Die Spannung ist das Maß für die Kraft, die auf die Elektronen aufgrund von Ladungstrennung wirkt.
Einschub: Es gibt neben der elektrischen Spannung auch eine mechanische Spannung. In diesem Text ist immer die elektrische Spannung gemeint. Das gilt auch für andere elektrische Größen. Diese werden einmalig als elektrische Größe eingeführt, anschließend spare ich mir aus Faulheit das Wort „elektrisch“.
Die elektrische Spannung ist mit der mechanischen Spannung einer Feder vergleichbar. Beide bewirken eine Kraft. Sie können sich eine geladene Batterie, die an ihren Klemmen eine elektrische Spannung aufweist, wie eine gespannte Feder vorstellen. Sie wartet nur darauf, dass die darin gespeicherte Energie freigesetzt werden kann.
Die Richtung der Spannung
Betrachten wir zwei Körper, auf denen jeweils Elektronenüberschuss herrscht. Auf Körper 1 sind 5 Elektronen zu viel, auf Körper 2 sind 3 Elektronen zu viel vorhanden.
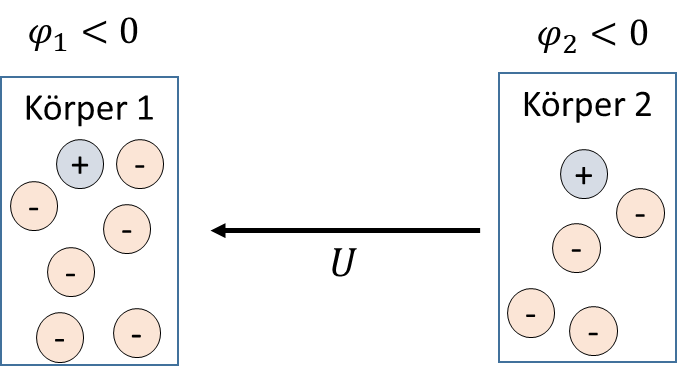
Beide Körper weisen ein negatives Potential auf, Körper 1 ist aber stärker negativ geladen als Körper 2. Deshalb wirkt eine Spannung, die von Körper 2 in Richtung von Körper 1 positiv ist. Die Spannung ist dann positiv, wenn der Pfeil vom relativ gesehen höheren zum niedrigeren Potential weist.
Wird zwischen diesen Körpern ein Weg für die Elektronen bereitgestellt, fließt aufgrund der Spannung ein Strom von Körper 1 in Richtung von Körper 2. Die Ladungen gleichen sich so aus, dass anschließend auf beiden Körpern 4 Elektronen zu viel vorhanden sind. Der Ladungsausgleich funktioniert also unabhängig von der Anzahl an Ladungen, er orientiert sich viel mehr am Unterschied zwischen Ladungen. Das Ergebnis eines Ladungsausgleichs sind also nicht immer zwei elektrisch neutrale ungeladene Körper, sondern zwei gleich geladene Körper. Dies gilt auch bei unterschiedlich großem Ladungsmangel zwischen zwei Körpern. Fehlen 10000 Elektronen auf Körper 3, während 9000 Elektronenauf Körper 4 fehlen, stellt sich nach einem Ladungsausgleich auf beiden Körpern ein Mangel von 9500 Elektronen ein.
Die Spannung bildet die Differenz aus zwei Potentialen. Betrachten wir ein Beispiel mit anderen Körpern mit anderen Ladungen:

Die Spannung kann auch anders herum eingezeichnet werden, dann gilt:
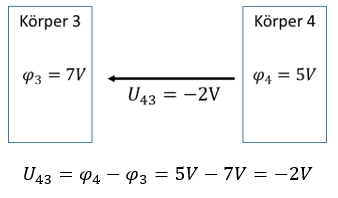
Im Ergebnis ändert das Umdrehen der Pfeilrichtung das Vorzeichen im Wert. Die Pfeilrichtung in Ihrer Skizze definiert also das Vorzeichen der Spannung.
Rechnen mit Potentialen und Spannungen
Beispiel: Wir betrachten ein System mit drei Körpern, die drei Potentiale aufweisen.
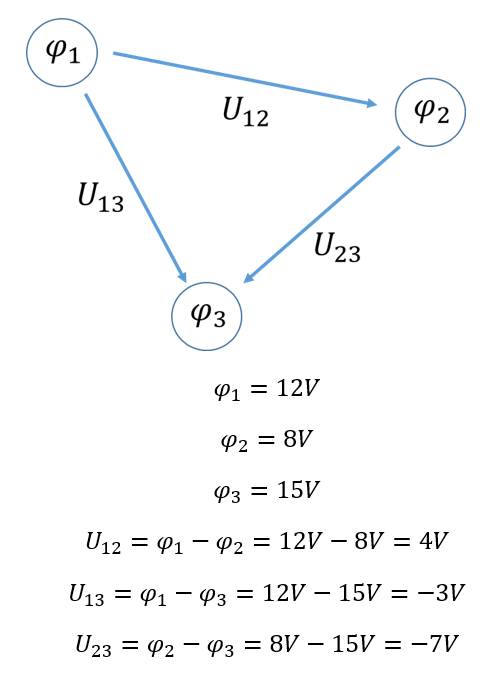
Die Spannungen werden anhand der in der Skizze angegebenen Pfeilrichtung berechnet.
Eine Spannung als Differenz zweier Potentiale ist einfach berechnet. Das Problem liegt in der richtigen Angabe der Richtung und des Vorzeichens. Das Vorzeichen ist immer richtig, wenn das Potential am Fußpunkt des Spannungs-Pfeils minus das Potential an der Spitze des Spannungspfeils gerechnet wird. Zeigt der Spannungspfeil vom größeren zum kleineren Potential, dann ist der Wert der Spannung positiv.
Wahl des Bezugspunkts
Es geht noch einfacher: Gehen wir gedanklich zurück zu dem Beispiel, in dem ein Stein hochgehoben wird und anschließend fallen gelassen wird. Angenommen der Stein wird auf h2 = 2m hochgehoben und fällt anschließend auf den Boden. Wir definieren dafür die Höhe des Bodens intuitiv als den Nullpunkt des Systems mit h1 = 0m.
Der Stein fällt um die Höhendifferenz Δh = h2 – h1 =2m – 0m = 2m nach unten. Wäre da aber kein Boden, würde der Stein tiefer herunterfallen. Der wahre Nullpunkt ist der Erdmittelpunkt, denn dort hin will der Stein eigentlich fallen, das ist der tiefste mögliche Punkt. Der Stein ist in Wahrheit etwa von der Höhe h2 = 6371002m auf h2 = 6371000m gefallen. In dem lokal begrenzten Experiment definieren wir aber den lokal tiefsten Punkt als Nullpunkt. Egal wo wir den Nullpunkt hinlegen, der Stein fällt um 2 Meter nach unten, denn die Differenz Δh = h2 – h1 beträgt in beiden Fällen 2m.
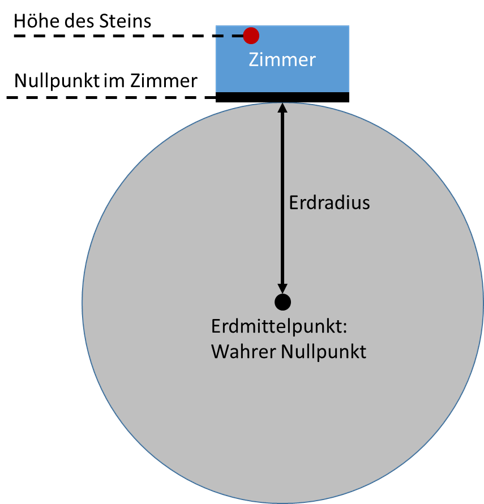
Mit Potentialen handhaben wir es in der Elektrotechnik genauso. Es gibt in einem System immer unterschiedliche Potentiale, denn Körper weisen alle unterschiedlich viel Ladung auf. Die Ladung zu bestimmen ist messtechnisch nicht einfach, wir können Ladungen nicht zählen und damit Potentiale nicht genau bestimmen. Die Potentialdifferenz, die Spannung, kann aber sehr einfach gemessen werden, und diese brauchen wir für die Lösung technischer Probleme.
Wie bei der Höhe des Steins ist die Wahl des Nullpunkts nicht entscheidend, so lange uns nur die Differenz Δh interessiert, um die der Stein heruntergefallen ist. In der Elektrotechnik interessiert uns das Potential eines Körpers ebenso wenig wie absolute Höhe eines Steins über dem Erdmittelpunkt. Uns interessiert nur die Spannung zwischen Körpern. Deshalb definieren wir normalerweise das niedrigste Potential als Nullpunkt, dann können wir einfacher rechnen.
Der Wert des niedrigsten Potentials wird zu φ = 0V definiert, so wie wir die Höhe des Bodens im Zimmer als h = 0m definieren. Beides ist physikalisch falsch, in beiden Fällen spielt das aber keine Rolle, denn wir wollen vor allem einfach rechnen. So wie wir von allen anderen Höhen den Erdradius von r = 6371000m abziehen müssen (ich nehme an, dass dies die Höhe des Bodens ist), so ziehen wir von allen anderen Potentialen den Wert des kleinsten Potentials ab, das wir als Nullpunkt ausgewählt haben.
Wir wählen im Beispiel oben das kleinste Potential φ2 als Nullpunkt und setzen φ2 = 0V. Dann ändern sich die anderen Potentiale zu
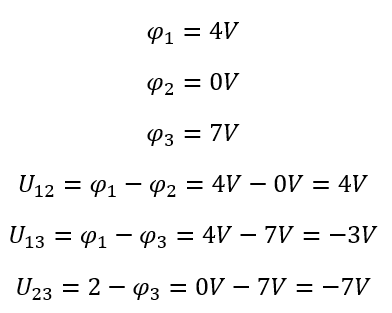
Die Spannungen werden wieder genauso aus der Differenz der Potentiale berechnet. Die Spannungen sind natürlich gleich groß wie vorher, denn wir haben nur von allen Potentialen das gleiche abgezogen. In der Differenz zweier Potentiale sieht man dies nicht.
In diesem System kann jetzt aber z. B. die Spannung U12 = φ1 – φ2 viel einfacher bestimmt werden, denn es gilt ja φ2 = 0V und damit U12 = φ1. In der Praxis werden viele Spannungen in einer elektrischen Schaltung auf den Nullpunkt bezogen. Dieser Nullpunkt ist so wichtig, dass er ein eigenes Schaltsymbol und eine eigene Bezeichnung bekommt: Die Masse. Dazu später mehr.
Negative Spannungen
Genau wie es unter dem Fußboden noch den Keller gibt, dessen Höhe geringer als die des Fußbodens ist, so kann es auch in Schaltungen Potentiale geben, die kleiner als der Nullpunkt sind. Dies ist teilweise so gewünscht. Darauf wird später eingegangen. Wichtig ist jetzt: Spannungen können positiv und negativ sein. Das Vorzeichen hängt davon ab, ob die Ladung größer oder kleiner als die Ladung der Masse ist. Die Masse ist die Referenz im System, die den Nullpunkt der Potentiale angibt.
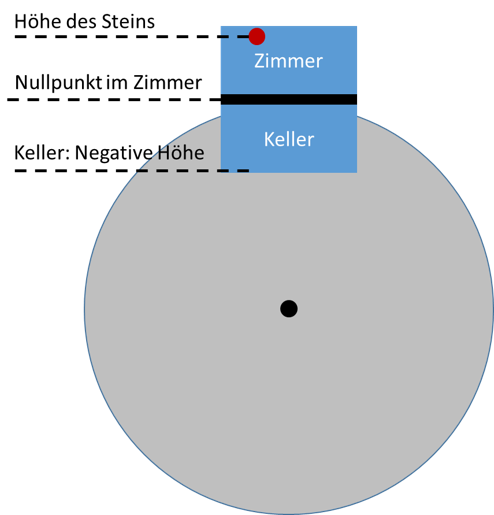
Addition von Spannungen
Wenn Batterien z. B. in einer Fernbedienung hintereinander verschaltet werden, dann addieren oder subtrahieren sich die Spannungen der Batterien. Dafür müssen wir die Anschlüsse auf die richtige Art verschalten. Das können wir mit Potentialdifferenzen erklären. Betrachten wir eine Amazon-Fernbedienung mit zwei AAA-Batterien. Jede AAA-Batterie weist eine Spannung von U = 1,5V auf.
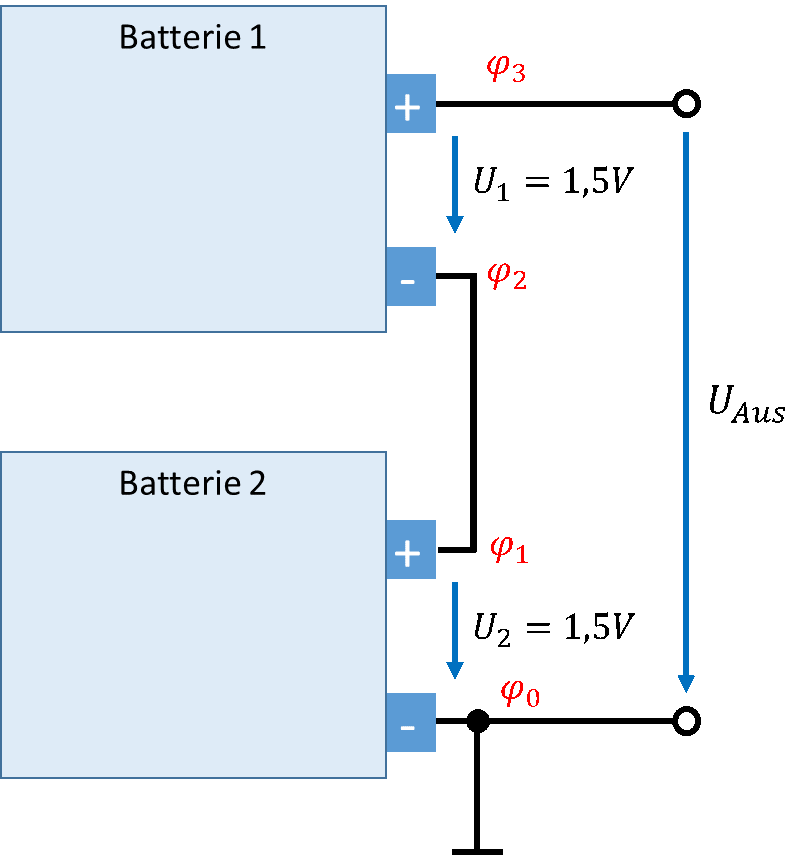
In schwarz sind Kabel oder Metallbleche gezeichnet, die in der Fernbedienung Anschlüsse der Batterien elektrisch leitfähig verbinden. Die schwarzen Kreise sind die Punkte, an denen wir weitere Schaltungsteile anschließen können. Die Elektronik der Fernbedienung wird rechts von den beiden Punkten angeschlossen. Die Batterien stellen nur eine Spannung für den Betrieb zwischen den beiden Punkten bereit.
Den Punkt mit niedrigstem Potential ganz unten definieren wir willkürlich als Bezugspunkt oder Masse. Damit beträgt dessen Potential φ0 = 0V. Die untere Batterie schiebt das Potential φ1 um 1,5V über das Potential φ0. Damit gilt φ1 = 1,5V.
Der obere Anschluss der unteren Batterie ist mit dem unteren Anschluss der oberen Batterie verbunden. Damit haben die beiden Anschlüsse das gleiche Potential. Wären diese Potentiale unterschiedlich hoch, würde sofort ein Ladungsausgleich stattfinden, bis die beiden gleich hoch sind. Also können wir bei elektrisch leitfähig verbundenen Körpern immer davon ausgehen, dass beide das gleiche Potential haben. Es gilt also φ2 = φ1 = 1,5V.
Das Potential φ3 wird von der oberen Batterie um 1,5V über das den Wert von φ2 geschoben. Damit beträgt dessen Potential φ3 = φ2 + 1,5V = 3V. Die Ausgangsspannung ist in der Zeichnung als Differenz der Potentiale φ3 und φ0 definiert. Damit gilt für die Ausgangsspannung UAus = φ3 – φ0 = 3V – 0V = 3V. Auf diese Weise schaffen wir es, die Fernbedienung mit 3V zu versorgen, obwohl wir nur 1,5V Batterien zur Verfügung haben. Hier nochmal die Zusammenfassung:
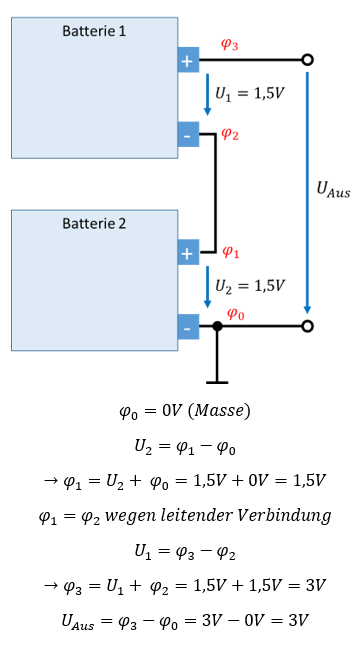
Setzen des Bezugspunkts
Jetzt setzen wir die Masse zwischen die beiden Batterien und schauen was sich verändert. Wir beziehen zwei neue Ausgangsspannungen auf die Masse.
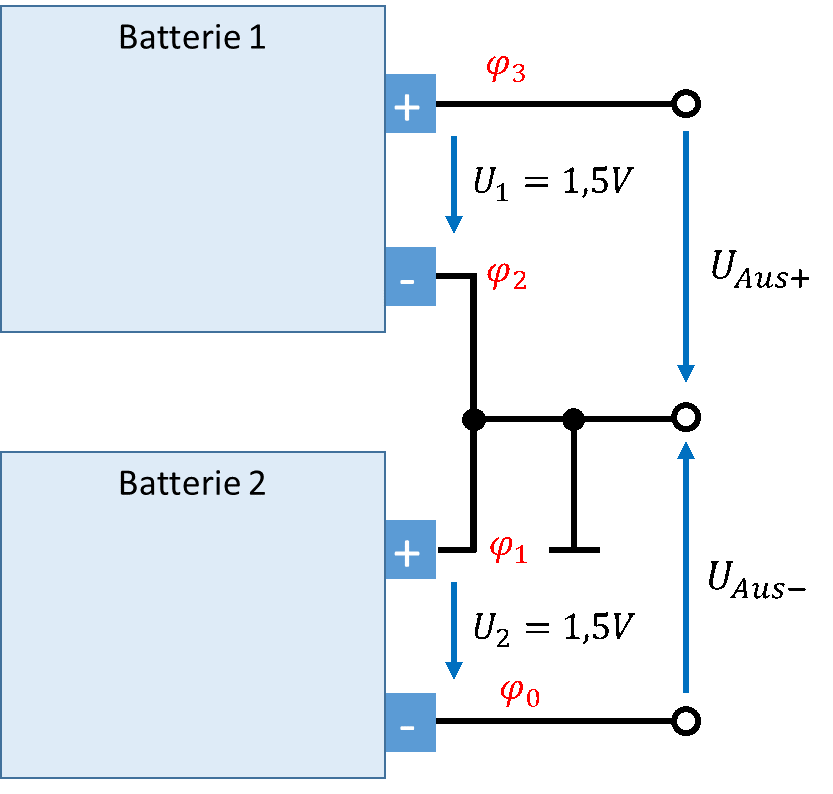
Durch die neue Festlegung der Masse gilt jetzt φ1 = φ2 = 0V. Die untere Batterie schiebt beide Anschlüsse um 1,5V auseinander. Weil jetzt der obere Anschluss per Definition den Wert φ1 = 0V hat, muss gelten φ0 = φ1 – 1,5V = -1,5V. Das Potential φ0 ist jetzt negativ (bezogen auf φ1).
An der oberen Batterie gilt weiterhin, dass φ3 von der Batterie um 1,5V über φ2 geschoben wird. Da φ2 = 0V gilt, gilt φ3 = 1,5V. Die Ausgangsspannung wird üblicherweise auf Masse bezogen. Es ergeben sich jetzt zwei Ausgangsspannungen, die wir jeweils mit der Pfeilspitze auf Masse einzeichnen. Es gilt UAus- = φ0 – φ1 = -1,5V – 0V = -1,5V. Und es gilt UAus+ = φ3 – φ2 = 1,5V – 0V = 1,5V. Hier nochmal die Zusammenfassung:
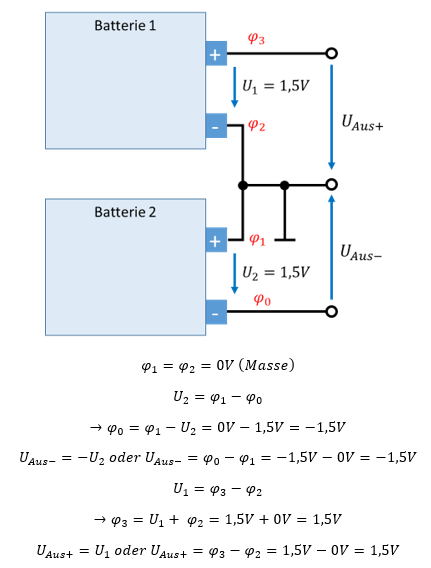
Wir haben mit den gleichen Batterien eine positive und negative Spannung bezogen auf Masse erzeugt. Negative Spannungen bekommen wir durch Verschiebung des Nullpunkts über das negativste Potential.
Weiter