Wir lösen uns jetzt vom Pendel und betrachten ein allgemeines geregeltes System. Schwingfähige Systeme schwingen bei einer Anregung von selbst, ohne dass von außen viel passieren muss. Regler sorgen dafür, dass die Regelgröße der Führungsgröße entspricht. Was passiert, wenn ein schwingfähiges System in einen Regelkreis eingebunden wird und die Führungsgröße konstant ist? Dann versucht der Regler, die Regelgröße konstant zu halten. Das System tendiert bei kleinster Anregung bereits zum Schwingen, was eine nicht konstante Regelgröße zur Folge hat. Wer gewinnt, der Regler oder die Schwingneigung?
Ein schwingfähiges System kennt zwei stabile Zustände. Es kann in Ruhe gehalten werden und sich einfach nicht „bewegen“. Oder es schwingt sinusförmig. Bei einer Schwingung können wir die Änderung des Spitzenwerts über der Zeit beeinflussen.
Ein „guter“ Regelkreis mit konstanter Führungsgröße versucht immer den Ruhezustand zu erreichen. Dafür reduziert er den Spitzenwert der Schwingung durch Dämpfung. Bei einer Anregung des Systems durch den Regler fängt es meistens erstmal an zu schwingen. Es ist eine der schwierigsten Aufgaben der Regelungstechnik, einen Regler so zu entwerfen, dass diese Schwingung gedämpft wird und die Regelgröße in möglichst geringer Zeit konstant wird.
Wenn die Führungsgröße einen Sollwertsprung vollzieht, also eine Heizung die Raumtemperatur z. B. von 20°C auf 25°C erhöhen soll, reagiert der Aktor mit einer geänderten Ansteuerung der Strecke. Das wirkt auf ein schwingfähiges System so, als wenn man ein Pendel anstößt. Es wird in Schwingung versetzt. Um das Problem zu analysieren zerlegen wir es in Teile und fügen es am Ende zusammen. Betrachten wir zunächst einen Teil des Regelkreises isoliert: Ein Aktor steuert eine Strecke in einem schwingfähigen System an.
Aktor und Strecke
Das Pendelbeispiel im Regelkreis ist zu kompliziert um es hier weiter zu betrachten. Deshalb lösen wir uns vom Pendel-Beispiel und betrachten allgemein einen Aktor mit P-Verhalten, der eine Strecke mit P-Verhalten ansteuert. Angenommen, die Regelgröße schwingt bereits gedämpft. Der Spitzenwert der Schwingung sinkt also mit der Zeit. Über den Aktor können wir die Schwingung entweder weiter dämpfen oder aufrechterhalten bzw. verstärken.
Um die Schwingung aufrechtzuerhalten, muss der Aktor in Phase zur Regelgröße agieren. Die Phasenverschiebung zwischen Aktor und Strecke muss 0 sein. Dann wirkt der Aktor immer so, dass die Regelgröße „gestützt“ wird.
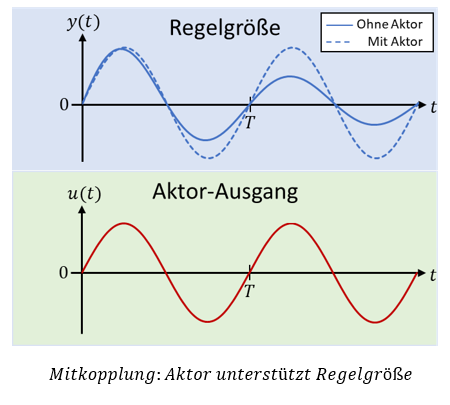
Der Aktor-Ausgang (rot) ist eine Größe, die über die Strecke auf die Regelgröße (blau) wirkt. Ohne Aktor würde der Spitzenwert der Regelgröße aufgrund der Dämpfung über der Zeit sinken (durchgezogene Linie). Weil der Aktor zu jeder Zeit in Richtung der Regelgröße eingreift, wirkt er der Dämpfung entgegen (gestrichelte Linie). In dem dargestellten Spezialfall entspricht die Energie, die der Aktor der Strecke hinzufügt, genau der Energie, die die Dämpfung der Strecke entzieht. Deshalb bleibt der Spitzenwert der Schwingung konstant. Übersteigt die eingebrachte Energie die Dämpfung, steigt der Spitzenwert mit der Zeit an. Wir sprechen von „Mitkopplung“, wenn der Aktor die Regelgröße unterstützt oder verstärkt.
Soll anders herum eine Schwingung durch den Aktor gedämpft werden, muss der Aktor gegenüber der Regelgröße um 180° Phasenverschoben agieren. Dann zieht der Aktor die Regelgröße immer in die Richtung, die der aktuellen Bewegung der Regelgröße entgegengesetzt ist.
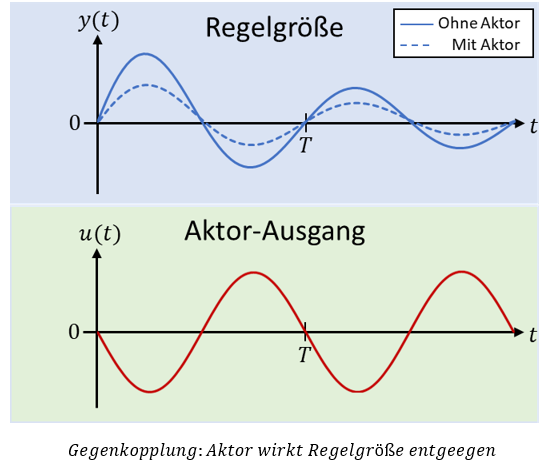
Beachten Sie die Phasenverschiebung zwischen Aktor und Regelgröße. Der Aktor wirkt entgegen der „Richtung“ der Regelgröße. Bei der Gegenkopplung wirkt der Aktor als zusätzliche Dämpfung. Der Spitzenwert der Schwingung sinkt durch den Eingriff schneller ab.
Aufgetrennter Regelkreis
Die Analyse von schwingfähigen Systemen muss den gesamten Regelkreis einbeziehen. Dafür wird der geschlossene Regelkreis an einer beliebigen Stelle aufgetrennt. Üblicherweise trennen wir ihn zwischen Ausgang der Strecke und Regelgröße auf. Wir erhalten damit eine Form der Berechnung, aus der wir direkt auf die Veränderung der Schwingung durch die Regelung schließen können:
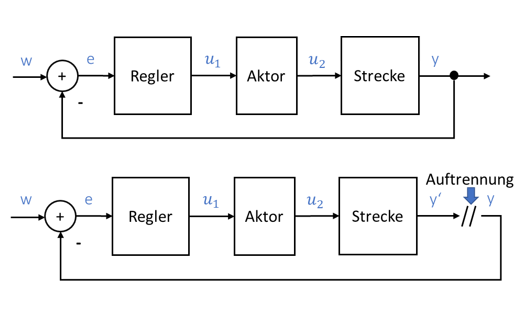
Die obere Abbildung zeigt den geschlossenen Regelkreis, der in der unteren Abbildung aufgetrennt wird. Links von der Auftrennung kommt die Größe y` aus der Strecke heraus. Die Größe y wird zurückgeführt auf den Eingang. Warum tun wir das? Wir können jetzt berechnen, wie sich die Größe y ändert, wenn sie einmal durch den Regelkreis hindurchläuft und als y` wieder herauskommt. Weil nur die Wirkung des Regelkreises interessiert, setzen wir die Führungsgröße zur Reduktion der Komplexität auf 0.
In der Praxis wird kein Regelkreis aufgetrennt oder unterbrochen, sonst funktioniert die Regelungstechnik nicht mehr. Das Auftrennen des Regelkreises ist nur ein mathematischer Trick, der zum Verständnis beiträgt. Es gilt:
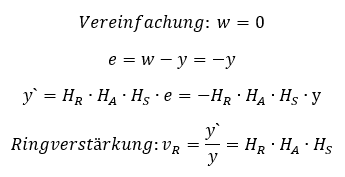
Die Veränderung des Signals y durch den Regelkreis erkennen wir am Quotienten aus y` geteilt durch y. Der Quotient wird am aufgeschnittenen Regelkreis als „Ringverstärkung“ bezeichnet. In die Ringverstärkung fließen alle Funktionsblöcke ein. Ist die Übertragungsfunktion eines Funktionsblocks kleiner als 1, dann dämpft er das Signal. Ist sie größer als 1, dann verstärkt er das Signal. Gleiches gilt auch für die Ringverstärkung als Produkt aller Funktionsblöcke.
Betrag der Ringverstärkung
Wenn die Ringverstärkung 1 beträgt, ändert sich das Signal beim Durchlauf durch den Regelkreis nicht. Dann gilt y` = y. Dämpfung und Verstärkung heben sich gegenseitig auf. Ist der Betrag der Ringverstärkung größer als 1, wird das Signal insgesamt verstärkt und es gilt y` > y. Der Spitzenwert einer Schwingung wird dann bei jedem Durchlauf durch den Regelkreis etwas größer. Ist der Betrag der Ringverstärkung kleiner als 1, sinkt der Spitzenwert einer Schwingung, weil das Signal insgesamt gedämpft wird.
Um dies grafisch zu verdeutlichen habe ich für unterschiedlichen Ringverstärkungswerte ein Signal vor dem Durchlauf durch den Regelkreis in rot und nach dem Durchlauf in blau dargestellt.
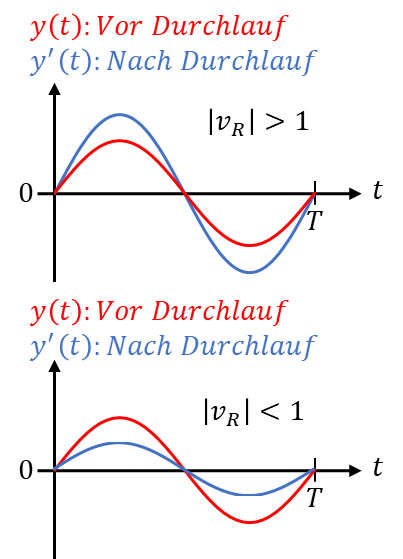
Wenn wir wissen, wie sich ein Signal bei einem Durchlauf durch den Regelkreis verändert, können wir sein Zeitverhalten bestimmen. Wird ein Signal bei einem Durchlauf kleiner, wird es mit der Zeit verschwinden. Wird es bei einem Durchlauf größer, wird es immer weiter ansteigen. Die Ringverstärkung zeigt uns, wie sich ein Signal über der Zeit verändern wird.
Phase der Ringverstärkung
Wir wissen bereits aus der Betrachtung von Aktor und Strecke, dass es wichtig ist, in welcher Phase ein Aktor eine Strecke „anstößt“. Ein Aktor kann eine Schwingung dämpfen oder verstärken, je nachdem wie Anregung und Schwingung zueinander verschoben sind. 0° Verschiebung bewirken eine Verstärkung, 180° Verschiebung bewirken eine Dämpfung. Wir können diese Erkenntnisse auf die Ringverstärkung übertragen:
Wenn ein Signal beim Durchlauf durch den Regelkreis keine Phasendrehung (0°) durchmacht, stößt sich das Signal selbst an, so dass die Schwingung verstärkt wird. Ist die Schwingung gerade positiv, wird sie noch positiver, weil sie sich selbst nach einem Durchlauf mit dem positiven Wert antreibt. Gleiches gilt, wenn die Phasendrehung n ∙ 360° beträgt.
Beträgt die Phasendrehung 180°, dämpft sich die Schwingung selbst. Ist die Schwingung gerade positiv, wird sie beim Durchlauf durch den Regelkreis negativ und reduziert sich selbst. Das gilt nicht nur bei 180°, sondern auch bei 180° + n ∙ 360°.
Jeder Regelkreis beinhaltet einen Subtrahierer im Eingang. Dieser dreht die Phase der Ringverstärkung immer um 180°. Ein Faktor –1 entspricht der Phasendrehung um 180°.
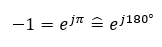
Schwingbedingungen
Eine Schwingung kann also nur dann dauerhaft aufrechterhalten werden, wenn zwei Bedingungen gelten:
1. Der Betrag der Ringverstärkung ist gleich 1. Damit bleibt der Spitzenwert der Schwingung konstant. Oder er ist größer als 1, dann steigt der Spitzenwert an.
2. Die Phase der Ringverstärkung beträgt 0° bzw. n ∙ 360°
Wenn ein Regelkreis nicht dauerhaft schwingen soll, müssen wir diese Bedingungen vermeiden. Das tun wir entweder durch Einstellung der Phase oder des Betrags der Ringverstärkung.
Speicher im Regelkreis
Jeder Speicher dreht die Phase zwischen Eingangs- und Ausgangsgröße um 90° oder π/2. Integratoren und Differenzierer drehen jeweils in unterschiedliche Richtungen. Bei sinusförmigen Signalen gilt:

Wenn zwei Integrierer im Regelkreis enthalten sind, wird die Phase insgesamt um 180° gedreht. Betrachten wir dafür die Ringverstärkung eines aufgetrennten Regelkreises mit I-Regler und I-Verhalten im Aktor:
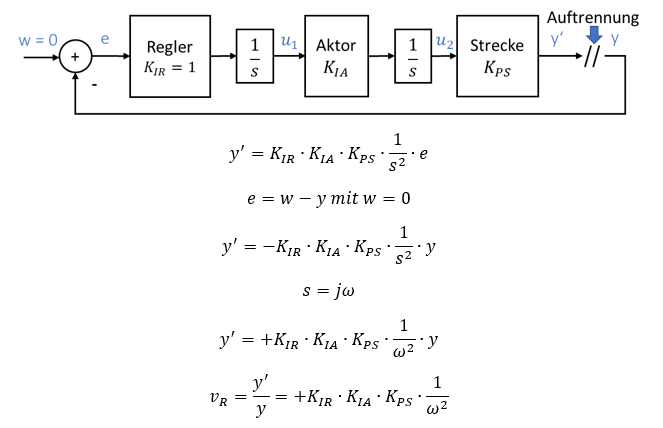
Das Minuszeichen im Subtrahierer dreht die Phase um 180°. Jeder Integrator dreht um -90° zurück. Damit ist die Phase der Ringverstärkung insgesamt 0°. Der Regelkreis ist mitgekoppelt. Das System schwingt.
Die Art der Schwingung hängt von den Parametern KIR, KIA und KPS ab.

Wir können den Betrag der Ringverstärkung über den Regler einstellen.
Es ist egal, an welcher Stelle im Regelkreis die Phase durch Speicher gedreht wird. Das kann auch in der Strecke passieren. Ein System ist auch schwingfähig, wenn zwei Differenzierer im Regelkreis enthalten sind. Ein I-Regler oder D-Regler verhalten sich ebenfalls wie Speicher. Ein System mit einem „echten“ Speicher und einem „Software“-Speicher im Regler ist ebenfalls schwingfähig. Es müssen nur mindestens zwei Speicher vorhanden sein.
Ein System mit einem Speicher ist prinzipiell nicht schwingfähig. Wir brauchen mindestens zwei Speicher, damit die Energie zwischen zwei Speichern hin- und herwechseln kann. Die Schwingung klappt auch mathematisch nicht, denn mit nur einem Speicher bekommen wir die Phase der Ringverstärkung nur um 180° ± 90° gedreht. Eine Drehung um insgesamt 0° bzw. 360° klappt so nicht.
Die Phasendrehung von Differenzierern und Integrierern können sich unter Umständen gegenseitig aufheben. Man kann z. B. mit einem D-Regler I-Verhalten in einer Strecke kompensieren. Das ist in theoretischen Regelkreisen gut möglich, in der Praxis ist es leider oft schwieriger.
Besonders rückgekoppelte Systeme neigen zum Schwingen, weil sie sich potentiell in der richtigen Phase selbst anstoßen können. Deshalb sind Regelkreise häufig schwingfähig. Wenn insgesamt zwei oder mehr Speicher in einem Regelkreis vorhanden sind, ist das geregelte System schwingfähig. Es ist dann Aufgabe der Regelungstechnik, die Schwingung zu unterdrücken. Das System wird bei einer Sprunganregung immer schwingen, aber wir können dafür sorgen, dass die Schwingung möglichst schnell abklingt.
Weiter