Ein reelles technisches System wird durch mathematische Gleichungen beschrieben. Gleichungen helfen beim Ausrechnen. Sie helfen aber wenig beim Verstehen. Für das Verständnis eignet sich ein Blockschaltbild besser. In einem Blockschaltbild wird ein System in Teilsysteme zerlegt.
Das Blockschaltbild besteht aus (Funktions-)Blöcken, die mit Signalen verbunden sind. Zur Vereinfachung betrachten wir in diesem Tutorial nur Blöcke mit einem Eingangs- und einem Ausgangssignal. Ein Block wird mathematisch durch die Übertragungsfunktion beschrieben. Es gilt

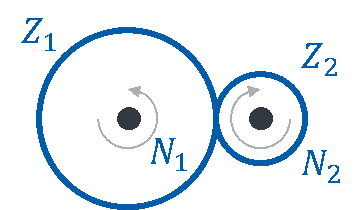
Beispiel eines Funktionsblocks: Getriebe
Ein Getriebe weist als Eingangsgröße die Drehzahl N1 an der Eingangsachse (schwarz) auf. Auf der Eingangsachse befindet sich ein Zahnrad (blau) mit Z1=20 Zähnen. Eine Ausgangsachse weist ein kleineres Zahnrad mit Z2=10 Zähnen auf. Es ist mit dem ersten Zahnrad verbunden. Die Drehzahl der Ausgangsachse N2 ist der Ausgang des Getriebes.
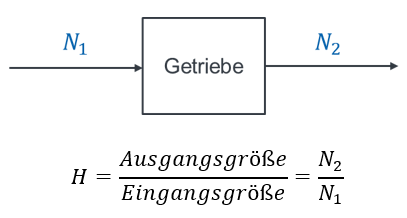
Das Getriebe wird als Block modelliert. Eingang des Blocks ist die Drehzahl N1. Ausgang ist die Drehzahl N2. Das Getriebe wird dadurch beschrieben, dass die Ausgangsdrehzahl auf die Eingangsdrehzahl bezogen wird. Der Block wird als Rechteck mit der Bezeichnung in der Mitte gezeichnet. Die Signale werden als Pfeile mit Bezeichner darüber gezeichnet.
Die Drehzahlen stehen in folgendem Zusammenhang mit der Anzahl der Zähne der Zahnräder:
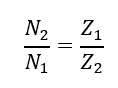
Damit können wir die Übertragungsfunktion unabhängig von den Werten an Ein- und Ausgängen beschreiben:
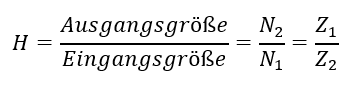
Das ist für die Modellierung wichtig, denn die Drehzahlen ändern sich, die Anzahl der Zähne der Zahnräder aber nicht. Die Übertragungsfunktion muss unabhängig von den aktuellen Werten der Eingangs- und Ausgangsgröße durch innere Größen definiert sein.
Mit der Übertragungsfunktion können Sie aus einer Eingangsgröße direkt die Ausgangsgröße ausrechnen. Durch Umstellen der Gleichung erhalten wir
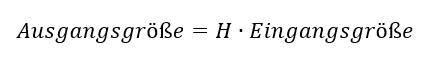
Für die Modellierung eines Blocks benötigen Sie also die Benennung von Ein- und Ausgangsgröße sowie den mathematischen Zusammenhang zwischen den beiden.
Addition und Subtraktion
Für ein Blockschaltbild müssen Signale addiert und subtrahiert werden. Diese mathematischen Operationen werden folgendermaßen modelliert:
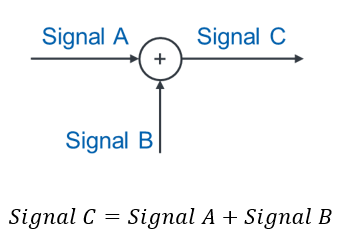
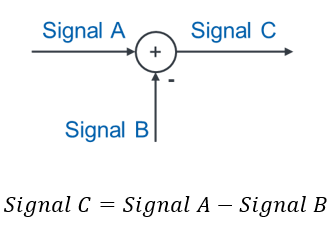
Soll subtrahiert werden, wird ein Minus-Zeichen an das Signal gezeichnet, das subtrahiert werden soll.
Multiplikation und Division
Wenn wir das Produkt zweier Größen modellieren wollen, dann fügen wir dafür einen Block mit einer Übertragungsfunktion ein. Der Faktor, mit dem multipliziert wird, entspricht dabei der Übertragungsfunktion H des Blocks. Wir schreiben den Zahlenwert des Faktors in den Block hinein. Soll z. B. Signal B mit Faktor 5 multipliziert werden, dann modellieren Sie das folgendermaßen:
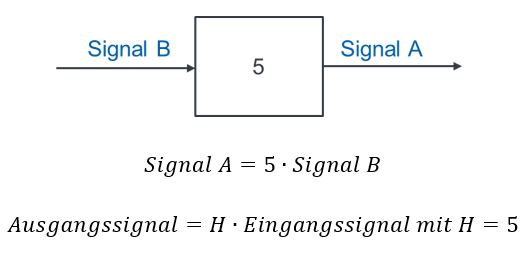
Wenn wir dividieren möchten, dann verwenden wir als Faktor H des Blocks einen Bruch. Um das Signal B durch 5 zu teilen nutzen Sie folgende Modellierung:
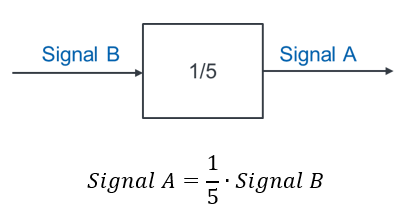
Beispiel 1
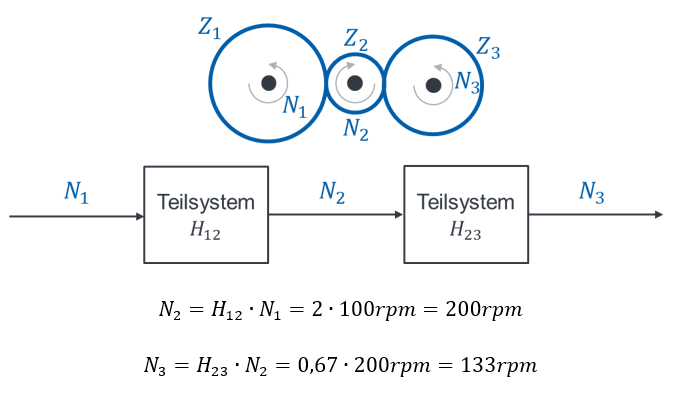
Betrachten wir ein zweistufiges Getriebe. Drei Zahnräder sind folgendermaßen zusammengeschaltet:
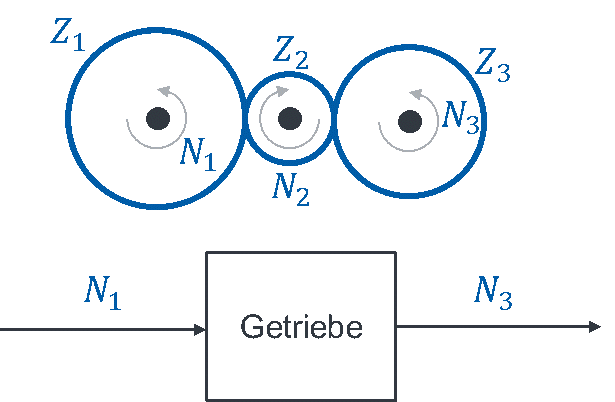
Eingangsgröße und Ausgangsgröße müssen in der Aufgabenstellung definiert sein, die kann man nicht „erkennen“. Die Eingangsgröße ist die Drehzahl N1 des linken Zahnrads. Die Ausgangsgröße des Getriebes ist die Drehzahl des rechten Zahnrads N3.

Berechnen wir die Übertragungsfunktion des Funktionsblocks „Getriebe“. Es gibt hier nicht die eine richtige Lösung, sondern das Getriebe kann unterschiedlich modelliert werden. Beginnen wir damit, jede der Stufen einzeln zu modellieren. Wir zerlegen das System in Teilsysteme und betrachten zunächst nur Zahnräder 1 und 2.
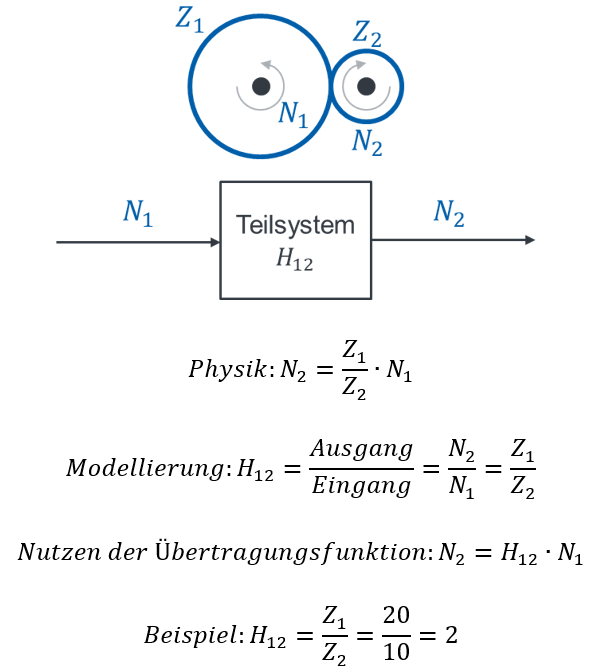
Anschaulich bedeutet die Lösung H = 2, dass sich Zahnrad 2 doppelt so schnell wie Zahnrad 1 dreht.
Anschließend betrachten wir das Teilsystem aus Zahnrad 2 und Zahnrad 3:
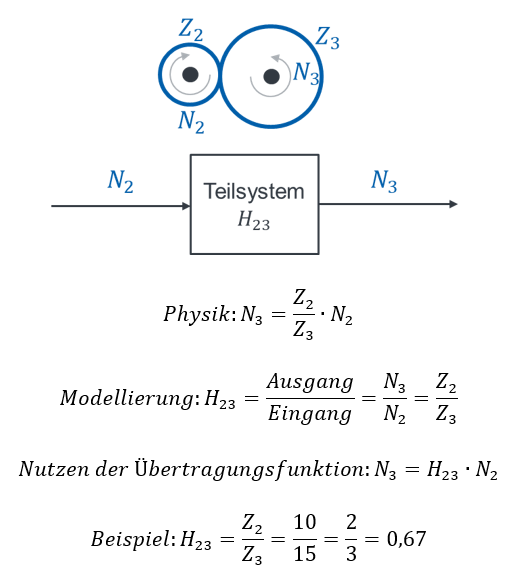
Wenn wir das Gesamtsystem modellieren wollen, dann bringen wir beide Teilsysteme zusammen. Sie werden hintereinandergeschaltet, weil die Ausgangsgröße von Teilsystem 1 die Eingangsgröße von Teilsystem 2 ist.
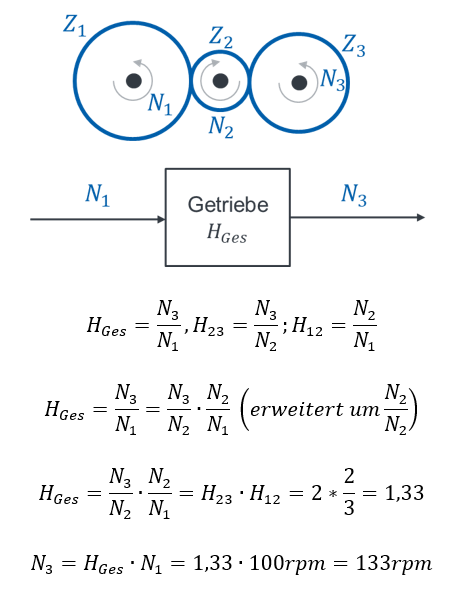
Als faule Ingenieure sind wir jetzt fertig. Wir können die Modellierung aber in diesem Fall noch vereinfachen. Wir können die Übertragungsfunktionen zu einer Gesamt-Übertragungsfunktion zusammenfassen. Das geht in diesem Fall einfach, weil beider Übertragungsfunktionen Faktoren sind:
Beispiel 2
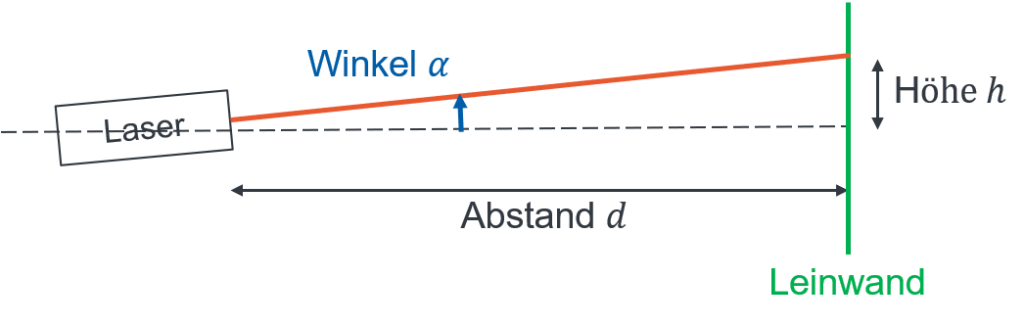
Wir betrachten einen drehbar gelagerten Laserpointer, der einen Punkt auf eine Leinwand projiziert. Wenn der Winkel des Laserpointers verändert wird, dann bewegt sich der Punkt auf der Leinwand. Die Eingangsgröße ist der Winkel α (mit dem wir in das System eingreifen) und die Ausgangsgröße ist die Höhe h des Punktes auf der Leinwand (die Auswirkung).
Wir brauchen immer etwas Physik zur Modellierung, sonst erhalten wir keine mathematischen Zusammenhänge. In Regelungstechnik-Prüfungen und in weiteren Übungsaufgaben wird die Physik immer vorgegeben. Es gilt für die Höhe h:
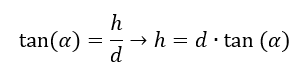
In diesem Beispiel haben wir eine Formel ermittelt, die man nicht einfach nach Ausgang geteilt durch Eingang umstellen kann. Der Winkel α ist im Tangens gefangen, den bekommen wir da nicht einfach raus. Mit dem Arcos-Tangens klappt das auch nicht, probieren Sie das mal. Deshalb nutzen wir die „Kleinwinkelnäherung“ aus der Mathematik. Für kleine Winkel gilt:
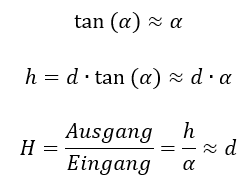
Damit können wir die Modellierung abschließen. Wir zeichnen das System im Blockschaltbild als Block mit seiner Übertragungsfunktion. Als Eingangsgröße geben wir den Winkel und als Ausgangsgröße die Höhe an.
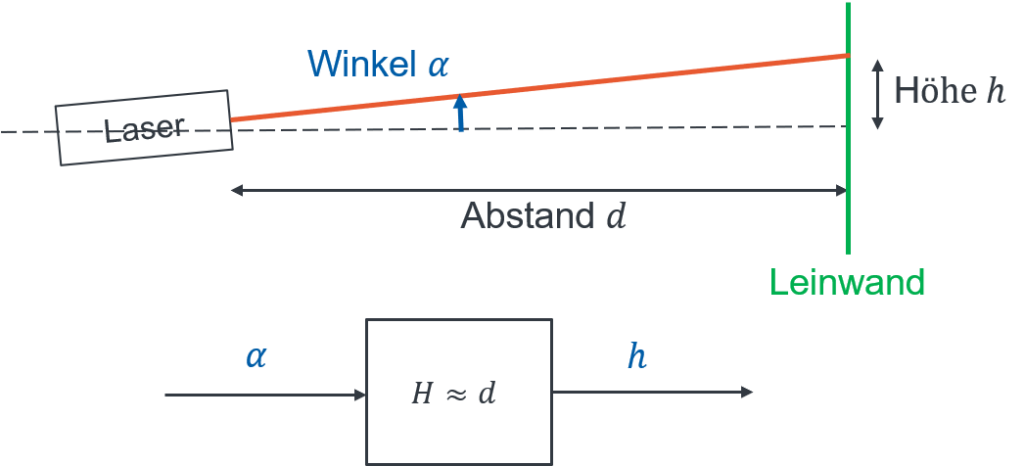
Das Ergebnis der Modellierung ist auch anschaulich plausibel. Wenn wir den Abstand d vergrößern, dann steigt bei gleichem Winkel α die Höhe h an.
Plausibilisierung
Wichtig: Bei jeder Modellierung muss das Ergebnis plausibilisiert werden. Das bedeutet: Variieren Sie den Eingang und überlegen Sie, wie sich der Ausgang verändern müsste. Dann rechnen Sie nach, ob das Modell in die richtige Richtung arbeitet. Wegen nicht plausibilisierten Modellen stürzen Brücken ein und Flugzeuge ab. Zu plausibilisieren ist die wichtigste Fähigkeit des Ingenieurs, gerade wenn wir Ergebnisse einer Modellierung durch künstliche Intelligenz betrachten.
Exakte Modellierung
Ein Modell bildet niemals exakt die Wirklichkeit ab. Deshalb ist es OK zu nähern, wenn wir uns dessen bewusst sind. Wir können im oberen Aufbau den Winkel α nicht beliebig genau vorgeben, weil nichts auf der Welt einen Laserpointer exakt und ohne Toleranzen dreht. Also brauchen wir auch keine perfekte und fehlerfreie Mathematik für die Modellierung.
In der Regelungstechnik geht es eher darum, dass das Modell das Verhalten des Systems grob abbildet. Die Erstellung exakter Modelle ist so aufwändig, dass dies in der Praxis nur selten gemacht wird. Wenn exakte Modellierung gefordert wird, dann holt man sich dafür einen Modellierungsexperten oder einen Regelungstechnik-Spezialisten und keinen ETR-Absolventen mit einem Semester Regelungstechnik im Gepäck.
Weiter