In einer Schaltung liegen unterschiedliche Potentiale vor. Betrachten wir die untere Schaltung als Beispiel. Oberhalb der Quelle liegt das höchste Potential in der Schaltung φ1 vor. Das Potential φ6 unterhalb der Quelle ist das niedrigste Potential.
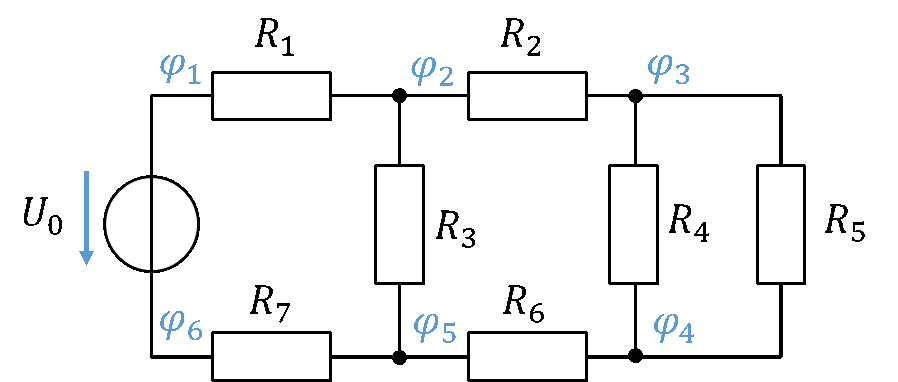
Durch den Widerstand R1 fließt der Strom I1. Dieser Strom führt dazu, dass nach Ohm´schen Gesetz die Spannung U1 über R1 abfällt.
Das Potential φ2 am nächsten Knoten ist also geringer als φ1 direkt an der Quelle. In der Analogie des Wassermodells ist das Potential φ1 die Höhe des Bergsees, an dem der Fluss entspringt. φ6 hat die Höhe des Meeresspiegels. Der Fluss fließt durch das erste Flussbett R1 in Richtung Meer. Dabei verliert er etwas an Höhe, die Höhe am Ende dieses Teils des Flussbetts muss also geringer sein als die des Bergsees.
Der Fluss teilt sich jetzt in zwei Arme I2 und I3 auf, deren Flussbette jeweils unterschiedlich sind. Das Potential φ5 ist niedriger als φ2, aber höher als φ6, denn der Strom ist in der Richtung von oben nach unten (von φ2 in Richtung φ5) durch den Widerstand R3 geflossen. An R3 ist dabei eine Spannung in Höhe von U3 = R3 ∙ I3 abgefallen. Je weiter man den Fluss in Fließrichtung (Stromrichtung) entlangläuft, desto geringer wird die Höhe (das Potential).
Die Maschenregel bringt in die Potentiale und Spannungen eine Systematik. Eine Masche ist dabei ein geschlossener Umlauf in einer Schaltung entlang einer Leitung, in dem jedes Bauelement und jeder Knoten nur einmal enthalten sein darf.
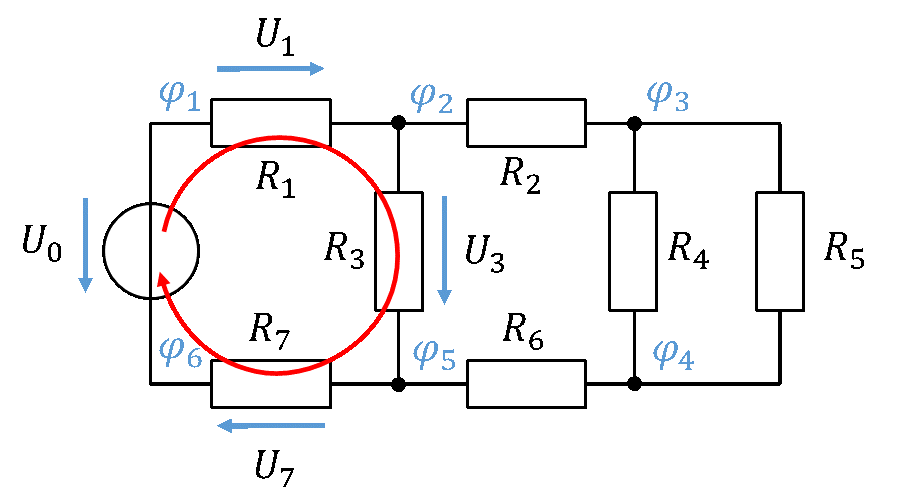
Der in Rot eingezeichnete Weg entlang von Leitungen bildet nach dieser Definition eine Masche, denn kein Bauteil im Umlaufweg wird mehrfach durchlaufen. In einer Masche gilt die Maschengleichung, nach der die Summe der Spannungen im Maschenumlauf gleich 0V ist. Dabei werden Spannungen im Uhrzeigersinn positiv, die gegen den Uhrzeigersinn negativ gezählt. In diesem Beispiel gilt für die rote Masche:
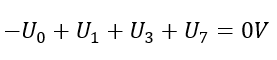
Wurden die Spannungen U0, U1 und U3 beispielsweise bereits berechnet, kann aus dieser Maschengleichung die Spannung
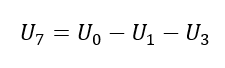
berechnet werden. Eine weitere Masche ist in der unteren Abbildung in grün eingezeichnet. Es gilt die Maschengleichung
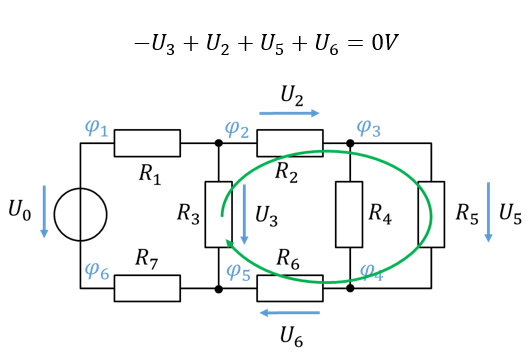
Es gibt in der Schaltung insgesamt 6 Maschen, aus denen teilweise redundante Gleichungen aufgestellt werden können. Es ist also wichtig, die richtige Masche zu finden, aus deren Gleichung der gesuchte Parameter abgeleitet werden kann.
Weiter