In den meisten realen Systemen sind mehrere integrierende bzw. verzögernde Komponenten enthalten. Diese erhöhen die Schwingneigung und verlangsamen das System. Differenzierendes Verhalten beschleunigt das System. Es ist naheliegend zu versuchen, mit D-Verhalten gezielt ungewollten I-Verhalten zu kompensieren. Es gilt:

Leider liegen die Terme oft nicht als reines I-Verhalten vor, sondern eher als PT-1-Verhalten. Dann gilt:

Bevor wir uns mit der Kompensation beschäftigen, betrachten wir zunächst das Systemverhalten eines Beispiel-Systems mit I-Verhalten und PT-1-Verhalten. Zunächst wird ein reiner P-Regler verwendet, ohne dass irgendein Verhalten kompensiert wird.
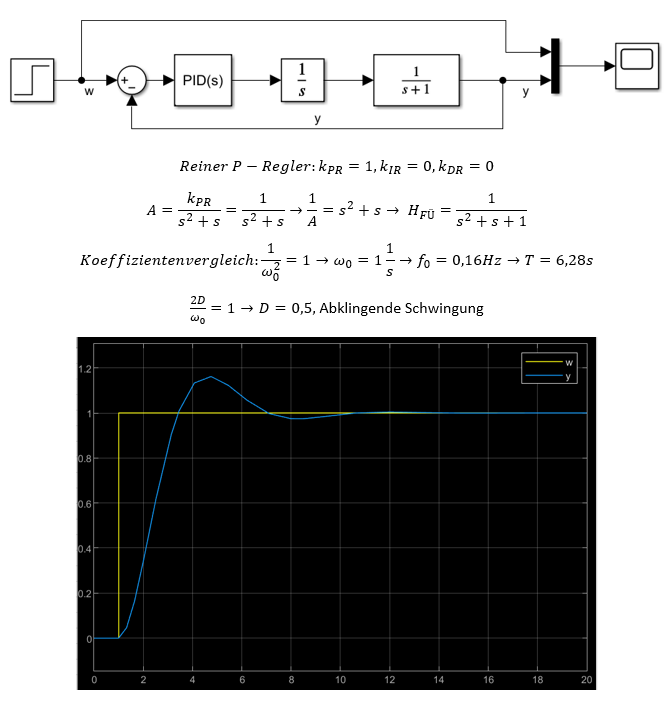
Kompensation des PT-1-Verhaltens der Strecke
Im ersten Schritt soll das PT-1-Verhalten der Strecke (ganz rechts) durch geeignete Wahl des Reglers kompensiert werden:

Frage: Wie kann der Kompensations-Term 1+s mit Hilfe eines PID-Reglers erzeugt werden? Dafür betrachten wir nochmal die Struktur eines PID-Reglers:
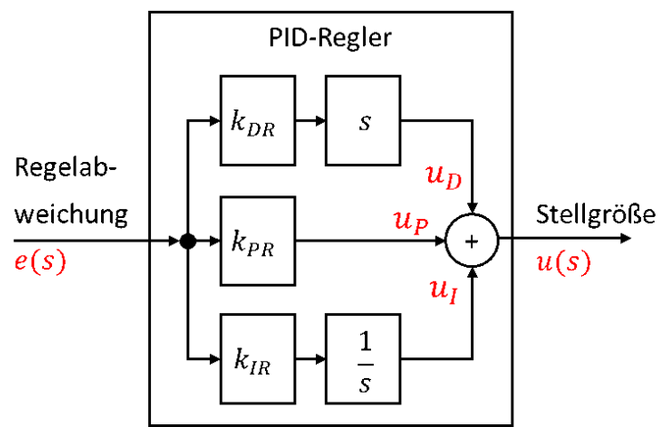
Der PID-Regler addiert an seinem Ausgang die Anteile P, I und D. Das führt zu folgender Übertragungsfunktion:
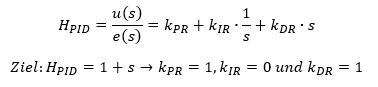
Insgesamt ergibt sich mit diesem Regler das gewünschte Verhalten. Hier nochmal die Zusammenfassung der Berechnung:
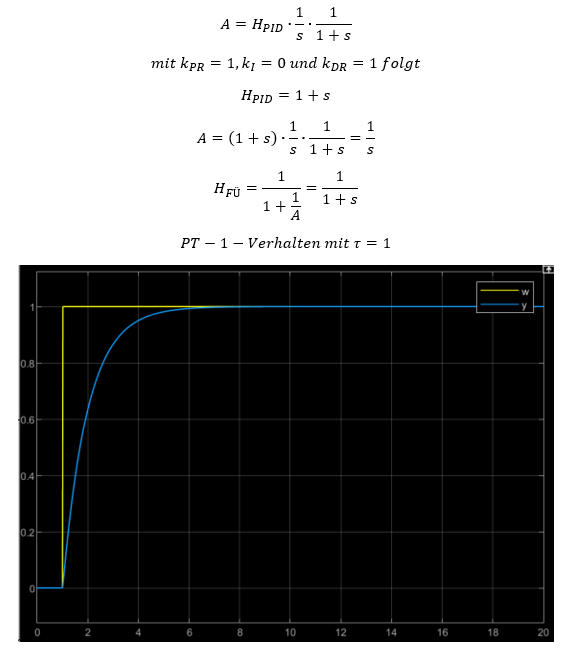
An der Sprungantwort des geregelten Systems sieht man, dass nur noch PT-1-Verhalten vorliegt. Der PID-Regler konnte über richtig dimensionierte P- und D-Anteile ein PT-1-Verhalten in der Strecke genau kompensieren. Das System verhält sich anschließend so, als ob in A nur noch reines I-Verhalten vorhanden wäre.
Kompensation des I-Verhaltens der Strecke
Als nächstes versuchen wir, das reine I-Verhalten aus der Strecke zu entfernen. Dann sollte nur noch PT-1-Verhalten in A übrigbleiben.
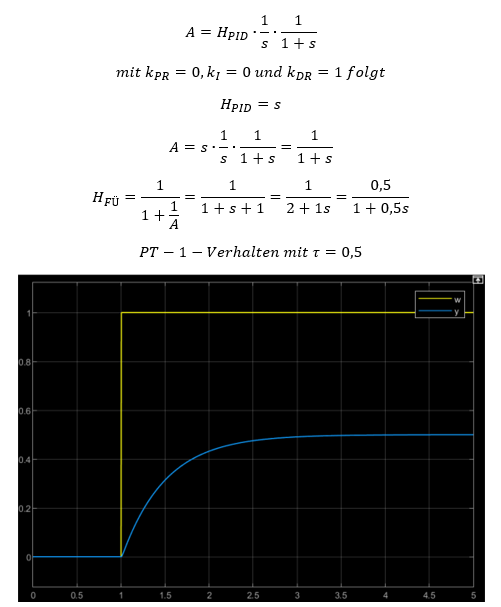
Es ist mit Hilfe eines reinen D-Reglers gelungen, das reine I-Verhalten der Strecke ideal zu kompensieren.
Fehlerhafte Kompensation
Für die Anwendung dieses Verfahrens muss das System sehr gut vermessen und modelliert worden sein. Beim PT-1-Verhalten muss Tau bekannt sein und es darf sich nicht ändern. Das Verfahren funktioniert in der Theorie sehr gut, in der Praxis ist der Einsatz schwieriger, weil die Systemparameter sich über Alterung, Verschleiß, Temperatur oder nichtlineares Systemverhalten ändern. Eine Kompensation kann nur mit exakter Kenntnis der Parameter funktionieren.
Zur Demonstration praktischer Probleme wird das Beispielsystem mit einem falsch konfigurierten Regler kompensiert. Wir versuchen wieder, das PT-1-Verhalten der Strecke zu kompensieren:
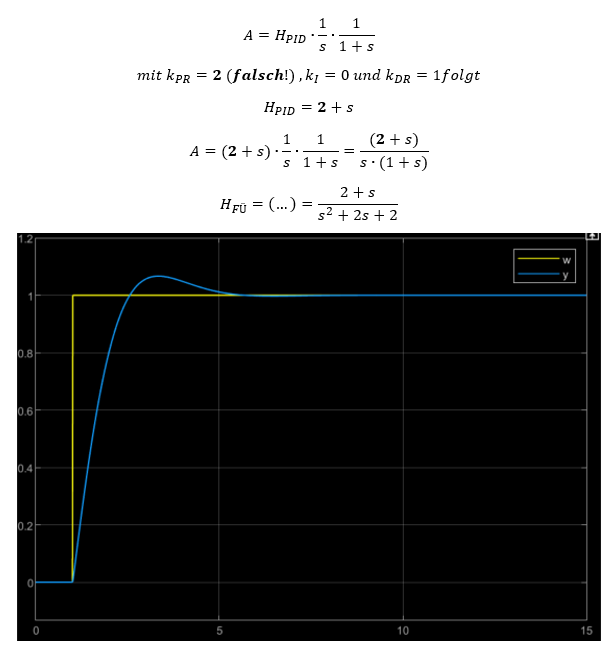
Das System zeigt bei falscher Kompensation wieder PT-2-Verhalten mit Überschwingen. Eine weiterführende Betrachtung von Polynomen im Zähler und Nenner des Führungsverhaltens geht für diese Vorlesung zu weit.
Ende