Zunächst betrachten wir Schaltungen, die aus einer Eingangsgleichspannung eine Ausgangsgleichspannung erzeugen. Der Hochsetzsteller wird genutzt, um eine Ausgangsspannung zu erzeugen, die größer als die Eingangsspannung ist. Dafür stehen Spule, Kondensator, Spannungsquelle und Schalter zur Verfügung.
Zunächst laden wir eine Spule mit Strom auf. Anschließend entladen wir sie in einen Kondensator. Damit fließt immer wieder Strom in den Kondensator. Dessen Spannung steigt während dieser Phasen an. Wenn ein Laststrom aus dem Kondensator herausfließt, sinkt seine Spannung wieder. Die Höhe der Ausgangsspannung wird also über eine Stromdifferenz aus zufließendem und abfließendem Strom am Kondensator bestimmt. Die Schaltung eines Hochsetzstellers sieht folgendermaßen aus:
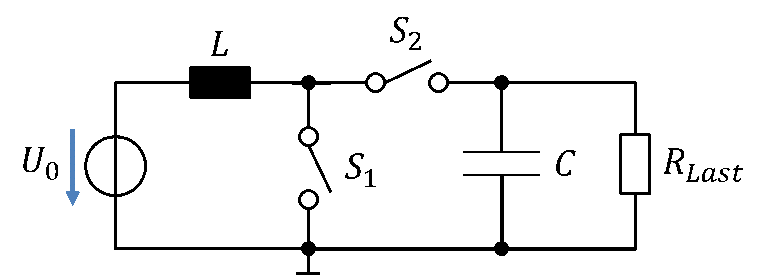
Betrachtung der Spule
Ignorieren wir den Lastwiderstand und den Kondensator zunächst. Die Schaltung besteht aus einer Quelle U0, die im Wassermodell der Pumpe entspricht. So wie die Pumpe Wasser auf eine bestimmte Höhe pumpt, hebt die ideale Spannungsquelle das Potential oberhalb der Quelle über Massepotential an. Die Gleichspannungsquelle baut eine Gleichspannung zwischen ihren Anschlüssen auf. Das Potential unten an der Quelle definieren wir als Masse.
Im ersten Fall (Zustand 1) ist Schalter 1 geschlossen und Schalter 2 offen. An der Spule fällt die Quellenspannung U0 ab. Der Strom fließt aus der Quelle über die Spule und Schalter 1 im Kreis. Dabei steigt der Strom in der Spule kontinuierlich an. Der stromführende Teil der Schaltung ist in Rot hervorgehoben. Wir gehen davon aus, dass zum Startzeitpunkt der Betrachtung kein Strom in der Spule fließt.
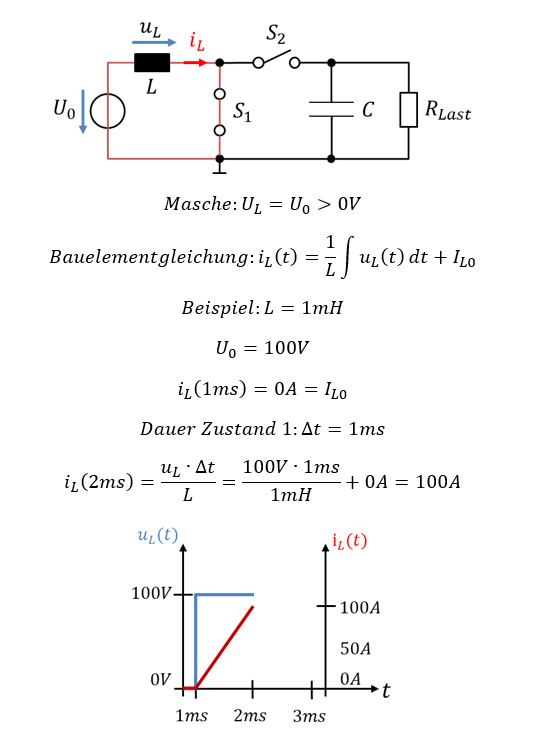
Die Spule wird 1ms lang mit Strom „geladen“. Dafür wird Zustand 1 für Δt = 1ms gehalten. Der Strom steigt an, während die positive Spannung von U = 100V an der Spule anliegt.
Wir schalten zum Zeitpunkt t = 2ms die Schalter um und wechseln in Zustand 2. Schalter 1 wird geöffnet und Schalter 2 wird geschlossen. Jetzt kommt der Kondensator ins Spiel. Den Lastwiderstand ignorieren wir weiterhin. Der Kondensator entspricht dem Tank im Wassermodell. Sein „Füllstand“ entspricht der Kondensatorspannung. Wenn Strom in den Kondensator fließt, steigt dessen Spannung an.
Wie im Wasserkreis betrachten wir den Fall, dass der Tank einen höheren Füllstand als die Pumpe hat. Der Kondensator ist also bereits auf z. B. UC = 190V aufgeladen. Der Wert ist willkürlich gewählt, am Ende werden Sie sehen worauf das hinausläuft. Betrachten wir erneut die Schaltung, Spannungen und Ströme:
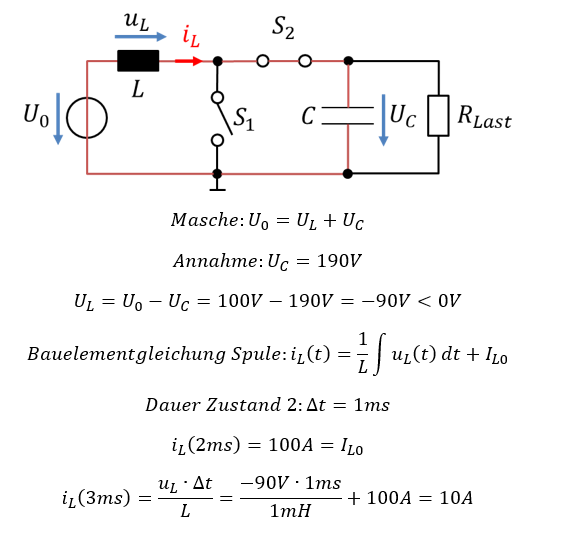
Die Kondensatorspannung ist höher als die Quellenspannung, also schiebt die Spule den Strom quasi „bergauf“. Es wird Energie von der Spule in den Kondensator geschoben, deshalb sinkt der Strom in der Spule in Zustand 2 von 100A auf 10A. Die Spule schiebt in Zustand 2 die ganze Zeit lang Strom in den Kondensator. Die Kondensatorspannung steigt an.
Schon diese relativ einfache Schaltung ist kompliziert zu berechnen. Wir müssen an den Speichern Integralgleichungen lösen. Das geht recht gut, so lange Spannung und Strom konstant sind, über die integriert wird. Das ist hier aber nicht der Fall. Die Kondensatorspannung steigt an, wenn die Spule Strom in den Kondensator schiebt. Damit ändert sich während der Integration die Spulenspannung, sie ist eigentlich nicht konstant wie oben angenommen. Der Spulenstrom sinkt also etwas weniger stark als angenommen.
Berücksichtigung des Kondensators
Der Spulenstrom sinkt halbwegs linear von 100A auf etwa 10A. Um den Anstieg der Kondensatorspannung zu berechnen, müssen wir dafür eine Funktion aufstellen und über diese mit Hilfe einer Stammfunktion integrieren. Das rechne ich Ihnen einmal vor:

Der Kondensator wird durch den Spulenstrom von 190V auf 210V aufgeladen. In dem Beispiel wird deutlich, dass die Spannung an der Spule problemlos von -100V auf +100V springen kann. Der Strom durch die Spule ändert sich aber nicht sprunghaft, sondern stetig.
Damit sind wir aber noch nicht fertig. Wir betrachten jetzt den Lastwiderstand RLast. Er liegt parallel zum Kondensator. Er steht stellvertretend für einen Verbraucher im Modell der Schaltung. Ein Verbraucher kann z. B. ein Heizelement, ein Motor oder ein Ladegerät für ein Elektroauto sein. Der Verbraucher wird als Ohm´scher Widerstand modelliert. Der Zusammenhang zwischen Spannung und Strom am Verbraucher folgt also dem Ohm´schen Gesetz.
Der Verbraucher zieht Strom aus dem Kondensator. Um diesen einfacher berechnen zu können nehmen wir an, dass die Kondensatorspannung über der Zeit konstant wäre. Wir haben gerade berechnet, dass sie nicht konstant ist, nehmen es aber zur Vereinfachung an. Die Kondensatorspannung beträgt im Mittel 200V. Ein Widerstand von RLast = 8Ω zieht damit einen konstanten Strom von ILast = 25A aus dem Kondensator. Damit sinkt dessen Spannung kontinuierlich über der Zeit. Den Kondensatorstrom berechnen wir aus der Knotengleichung am Knoten oberhalb des Kondensators:
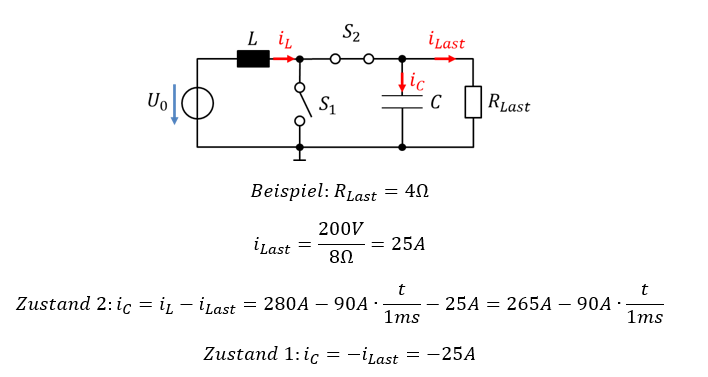
Im zeitlichen Mittel wird durch den Widerstand 25A Strom aus dem Kondensator gezogen. Während Zustand 2 wird ein mittlerer Strom von etwa 50A von der Spule auf den Kondensator geschoben. Zustand 1 und Zustand 2 dauern gleich lange. Also ist im zeitlichen Mittel der zugefügte Strom gleich dem entnommenen Strom. Das System ist somit stabil, und die Spannung am Kondensator sowie der Laststrom sind tatsächlich etwa konstant.
Simulation
Es wird deutlich, dass eine manuelle Berechnung der Vorgänge in der Schaltung ziemlich komplex ist. Dazu kommt, dass viele Annahmen für eine Vereinfachung gemacht werden mussten. In solchen Situationen macht es Sinn, in eine Simulation zu wechseln und sich von dieser vorrechnen zu lassen, wie so eine Schaltung funktioniert. Ich demonstriere das in LT-Spice, einer frei verfügbaren Simulations-Software.
Wir ersetzen die idealen Schalter zunächst durch reale Schalter. Der untere Schalter S1 wird als Mosfet oder IGBT ausgeführt. Er muss aktiv geöffnet und geschlossen werden. Der zweite Schalter wird als Diode ausgeführt. Er wird vom Stromfluss durch die Diode geschaltet. Immer wenn S1 geschlossen ist, ist die Diode gesperrt (Spannungsrichtung). Der Spulenstrom fließt dann von der Quelle durch S1. Ist S1 offen, treibt die Spule den Strom durch die Diode und öffnet diese.
Zunächst der Schaltplan in LTSPICE:
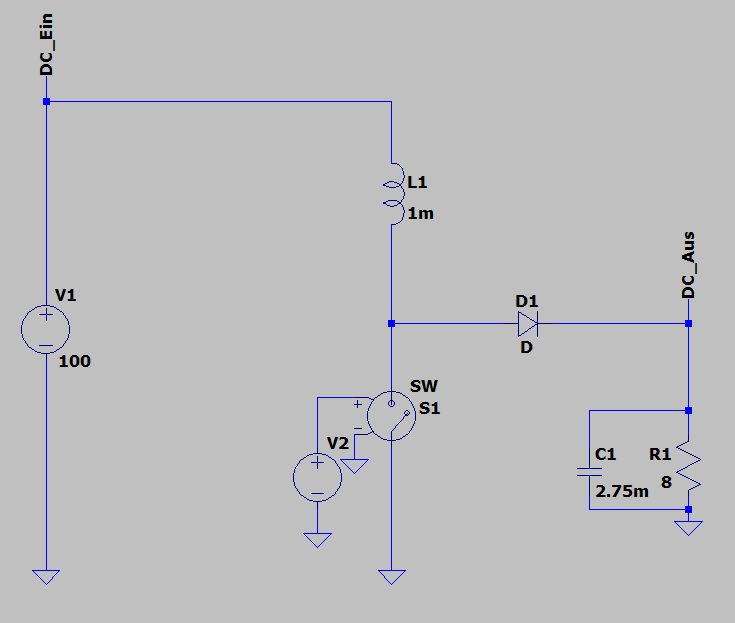
Links sehen Sie die Eingangsquelle V1. Es folgen Spule L1, Diode D1 und die Last aus R1 und C1. Der Schalter S1 wird von einer Steuerquelle V2 angesteuert. Je nach Spannung an V2 ist S1 offen oder geschlossen.
Der Schalter S1 wird periodisch betätigt. Jede Millisekunde wird zwischen Zustand 1 und 2 gewechselt. Deshalb wird als Ansteuerquelle für Schalter S1 ein PWM-Signal mit f = 500Hz eingesetzt.
In der unteren Abbildung ist der Zeitverlauf von Spannung am Kondensator und Strom der Spule im eingeschwungenen Zustand zu sehen.
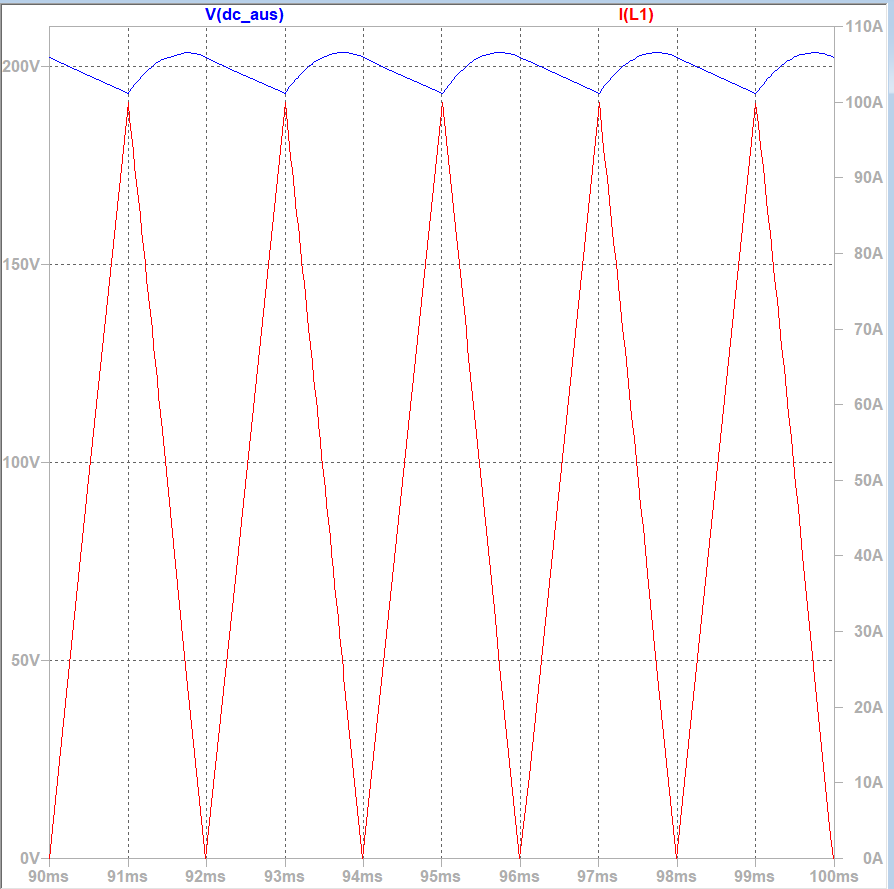
Auf der linken Y-Achse sehen Sie die Spannung (blau) am Kondensator aufgetragen. Auf der rechten Y-Achse den Strom (rot) durch die Spule. Der Strom liegt in der Simulation zwischen 38A und 42A. In der Berechnung schwankt er zwischen 10A und 100A, weil nicht berücksichtigt wurde, dass die Kondensatorspannung nicht konstant ist. Die Kondensatorspannung steigt und fällt zwischen den Werten 190V und ca. 210V. In der Simulation ist berücksichtigt, dass der Laststrom die Kondensatorspannung kontinuierlich sinken lässt.
In der Simulation sind alle realen Effekte berücksichtigt, die wir in der Rechnung vernachlässigt haben. Sie ist der Berechnung erstaunlich ähnlich. Also haben wir wahrscheinlich in der Simulation und in der Rechnung keinen groben Fehler gemacht.
Eine Simulation muss immer mit einer Rechnung oder einer Messung verifiziert werden. Sonst haben Sie keine Chance, Fehler in der Simulation zu finden. Sie müssen das Ergebnis vor der Simulation ungefähr kennen. Dafür überlegen Sie, welche Größen etwa konstant bleiben und halten diese für die Rechnung konstant. Damit machen Sie zwar einen Fehler, aber keinen großen. Das geht insbesondere bei Größen, die sich um einen Mittelwert herum ändern, wie oben im Beispiel die Kondensatorspannung. Wenn die Simulation am Ende bis auf ca. ±20% an das Rechenergebnis herankommt, dann haben Sie wahrscheinlich richtig simuliert.
Der Kondensator
Die Rolle der Spule als Schwungrad ist im letzten Kapitel deutlich geworden. Was tut der Kondensator in der Schaltung? Im Wassermodell stellt der Kondensator einen Tank oder Wasserspeicher dar. Wird Wasser hineingefüllt (positiver Strom), steigt der Füllstand (Spannung) an. Wird Wasser entnommen (negativer Strom), sinkt der Füllstand (Spannung).
Er verhält sich in allem reziprok zur Spule. An einem Kondensator ändert sich die Spannung stetig, der Strom kann sich sprunghaft ändern. Eine Spule wird eingesetzt, um einen Strom zu glätten. Mit einem Kondensator glätten wir eine Spannung.
Obwohl der Strom in den Kondensator dreiecksförmig verläuft, ist die Spannung am Kondensator relativ konstant. Je höher die Kapazität des Kondensators ist, desto geringer ist die Spannungsänderung durch den Strom. Es gilt:
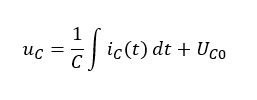
Je größer C ist, desto weniger stark ändert sich uC mit dem Strom iC. Dann dominiert in der Gleichung oben die Spannung UC0, die vor dem Stromfluss bereits im Kondensator enthalten war.
Der Kondensator als Speicher entkoppelt den Spulenstrom vom Laststrom. Die Spule schiebt nur in Zustand 2 Strom in den Kondensator. Der Lastwiderstand zieht kontinuierlich Strom aus dem Kondensator. Was immer an Strom hin- und hergeschoben wird, die Spannung bleibt halbwegs konstant.
Variation der Ansteuerung
Bisher haben wir beide Zustände gleich lange laufen lassen. Wenn Zustand 1 länger und Zustand 2 kürzer eingenommen wird, steigt der Strom länger an als er sinkt. Damit steigt der Ausgangsstrom. Es wird mehr Strom in den Kondensator reingeschoben als rausgezogen. Deshalb steigt die Ausgangsspannung an. Über die Variation der Dauer der Zustände kann die Höhe der Ausgangsspannung variiert werden. Das können Sie simulieren oder als Schaltung aufbauen. Das tun wir in der Vorlesung.
Zusammenfassung
Wir haben eine Schaltung aus Spule, Kondensator und Schaltern gebaut, mit der eine Ausgangsspannung für eine Last erzeugt wird, die größer als die Eingangsspannung ist. Dafür „laden“ wir die Spule mit Strom auf und lassen sie sich anschließend in den Kondensator hinein „entladen“. Dies ändert die Spannung des Kondensators.
Fassen wir die wichtigsten Erkenntnisse dieses Kapitels zusammen:
1. Spulen verhalten sich wie drehende Schwungräder, mit denen Ladung in Schaltungen bewegt werden. Aufgrund der Trägheit ändert sich der Strom durch eine Spule nur stetig und nur dann, wenn von außen eine Spannung an der Spule angelegt wird.
2. Der Spulenstrom steigt an, wenn die Spannung in Stromrichtung positiv ist. Das entspricht Wasser, das entlang des Schwungrads bergab fließt und damit das Schwungrad antreibt. Der Spulenstrom sinkt, wenn die Spannung in Stromrichtung negativ ist. Das entspricht Wasser, das vom Schwungrad bergauf geschoben wird und damit das Schwungrad bremst. Die Spannung an der Spule entspricht der Steigung des Wassers.
3. Mit einer Spule, einem Kondensator und zwei Schaltern kann eine Schaltung gebaut werden, die aus einer Eingangsgleichspannung eine höhere Ausgangsgleichspannung erzeugt.
4. In einem komplexen System weichen wir auf Simulation aus, wenn die Berechnung mathematisch zu schwierig wird. Wir brauchen Überschlagsrechnungen, die auf Näherungen basieren, um die Simulation zu verifizieren. Für diese Abschätzungen setzen wir nur leicht veränderliche Größen als konstant an.
Die Ausgangsspannung der Schaltung ist höher als die Eingangsspannung. Wir bezeichnen diese Schaltungstopologie als „Hochsetzsteller“. Über die Ansteuerdauer der Zustände können wir die Höhe der Ausgangsspannung variieren.
Weiter