I-Verhalten beschreibt integrierendes Verhalten. Ein System weist I-Verhalten auf, wenn seine Ausgangsgröße dem Integral der Eingangsgröße über der Zeit entspricht. Speicher integrieren den Zulauf auf, deshalb weisen Speicher I-Verhalten auf.
Speicher können gut mit dem Wassermodell beschrieben werden. Wasserspeicher werden über die Parameter Zulauf, Ablauf und Füllstand beschrieben. Der einfachste Speicher ist der mit Wasser gefüllte Eimer. Zu Einsatzmöglichkeiten und der Mathematik, mit der sie beschrieben werden, siehe Kapitel Speicher. Speicher weisen folgenden Zusammenhang zwischen Eingang und Ausgang auf:
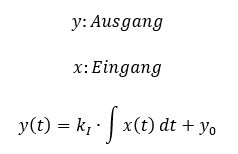
Die Übertragungsfunktion H ist über der Zeit nicht konstant, denn es kommt die Zeit t im Zusammenhang zwischen Eingang und Ausgang vor. Der Faktor kI wird später betrachtet. Vereinfachen wir das Verhalten zunächst einmal, indem wir x(t) auf einen konstanten Wert setzen. Das ist keine allgemeine Lösung mehr, sondern eine starke Vereinfachung.
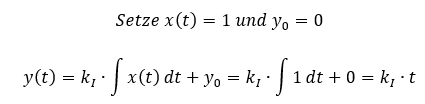
Wird eine Größe über der Zeit integriert, dann wird diese aufsummiert. Wenn der Zulauf eines Speichers konstant ist, dann steigt dessen Füllstand linear an. Das sehen wir oben in der Vereinfachung für x(t) = 1. Es ergibt sich ein proportionaler Zusammenhang zwischen der Ausgangsgröße y(t) und der Zeit t.
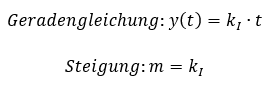
Sprungantwort
Bei einer Sprunganregung im Eingangssignal springt x(t) von 0 auf 1. Während x(t) = 0 gilt, bleibt der Ausgang y(t) unverändert. Ein Speicher ohne Zulauf ändert seinen Füllstand nicht. Nach dem Sprung gilt x(t) = 1, so wie in der Vereinfachung weiter oben. Es ergibt sich folgende Sprungantwort:
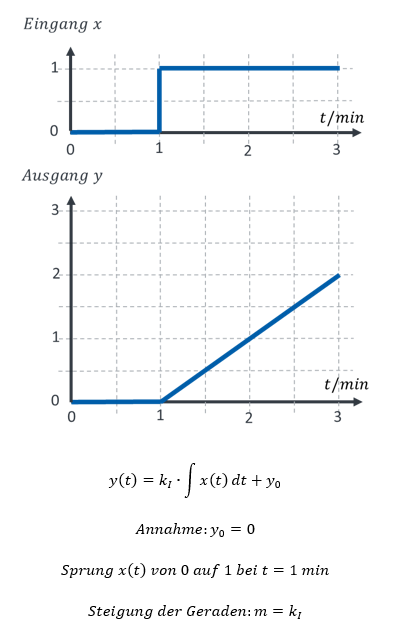
Die Steigung der Gerade ist charakteristisch zur Beschreibung des I-Verhaltens. Sie wird allgemein als kI bezeichnet. Konkrete Speicher weisen unterschiedliche Werte von kI auf.
Aus der Sprungantwort eines Speichers können wir zwei Erkenntnisse ziehen:
1. Die Sprungantwort ist eine Gerade. Es handelt sich also um I-Verhalten.
2. Die Steigung der Geraden entspricht dem charakteristischen Parameter für I-Verhalten: kI.
Der Parameter y0 gibt an, welchen Wert der Ausgang hatte, bevor die Integration startet. Er beschreibt z. B. den Füllstand eines Eimers, bevor der Zulauf geöffnet wird. Integriert wird dann nur über den Zulauf. Der neue Füllstand ergibt sich aber aus dem alten Füllstand plus dem Integral aus dem Zulauf über der Zeit.
Beispiel Auto
Wir betrachten eine Autofahrt in den Urlaub. Eingangsgröße ist die Geschwindigkeit des Autos v. Ausgangsgröße ist die bereits gefahrene Strecke s. Wenn ein Auto mit konstanter Geschwindigkeit fährt, dann wird die gefahrene Strecke immer größer. Wenn das Auto anhält, dann ist die bereits gefahrene Strecke nicht 0, sondern sie bleibt unverändert. Das ist typisch für I-Verhalten: Wenn die Eingangsgröße 0 beträgt, ist die Ausgangsgröße nicht 0 (wie bei P-Verhalten). Die gefahrene Strecke hängt von der Geschwindigkeit ab, mit der Sie in der Vergangenheit bereits gefahren sind. Es gilt:

Der Wert von kI entspricht dem Vorfaktor vor dem Integral. In diesem Beispiel beträgt dieser 1.
Beispiel Eimer
Am Eimer gilt:
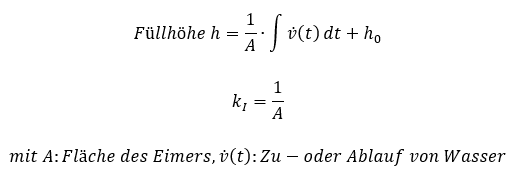
Beispiel bewegte Masse
Eine Masse wird von einer Kraft F bewegt. Ich kann einen Fußball der Masse m mit einer Kraft F in Bewegung v versetzen. Wie verhält sich so eine Bewegung mathematisch? Bewegte Massen zeigen I-Verhalten.
Ein bewegter Körper bewegt sich mit konstanter Geschwindigkeit (Ausgang ≠ 0) weiter, wenn keine äußeren Kräfte (Eingang = 0) auf ihn wirken. Das ist ein sicheres Zeichen für I-Verhalten. Die Erde fliegt z. B. mit konstanter Geschwindigkeit um die Sonne herum, ohne dass Kräfte diese beschleunigen. Dass Körper im Flug langsamer werden liegt an äußeren Kräften wie der Reibung.
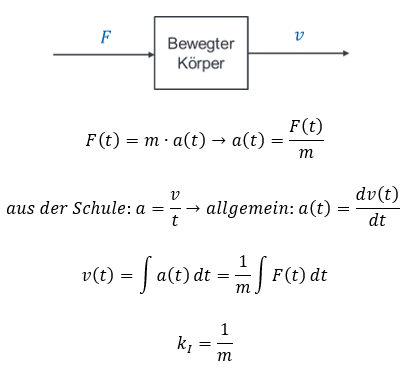
Der Eingang eines solchen Systems ist eine Kraft, die von außen auf den bewegten Körper wirkt. Der Ausgang ist seine Geschwindigkeit. Es gilt:
Beispiel Kondensator
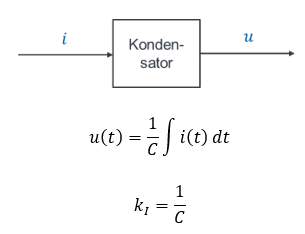
In der Elektrotechnik werden Kondensatoren und Spulen als Speicher eingesetzt. Am Kondensator gilt:
Systeme mit Ausgleich
Theoretisch steigt der Ausgangswert bei einem Speicher immer weiter an, so lange ein Eingangswert anliegt. Der Füllstand des Eimers steigt immer weiter an, so lange Wasser zuläuft. In der Praxis geht das natürlich nicht. Der Eimer läuft über, wenn er voll ist und noch mehr Wasser hineinfließt. Das gilt üblicherweise an beiden Grenzwerten nach oben und nach unten. Einen leeren Eimer können Sie auch nicht weiter entleeren.
Den Effekt des Überlaufens bezeichnen wir als „Ausgleich“. Ein Speicher mit Ausgleich strebt bei vollständiger Befüllung einen konstanten Endwert an. Bis zur vollständigen Befüllung oder Leerung zeigt er integrierendes Verhalten.
Betrachten wir die Sprungantwort eines Beispielsystems mit I-Verhalten und einen Ausgleich beim Wert 1,5:
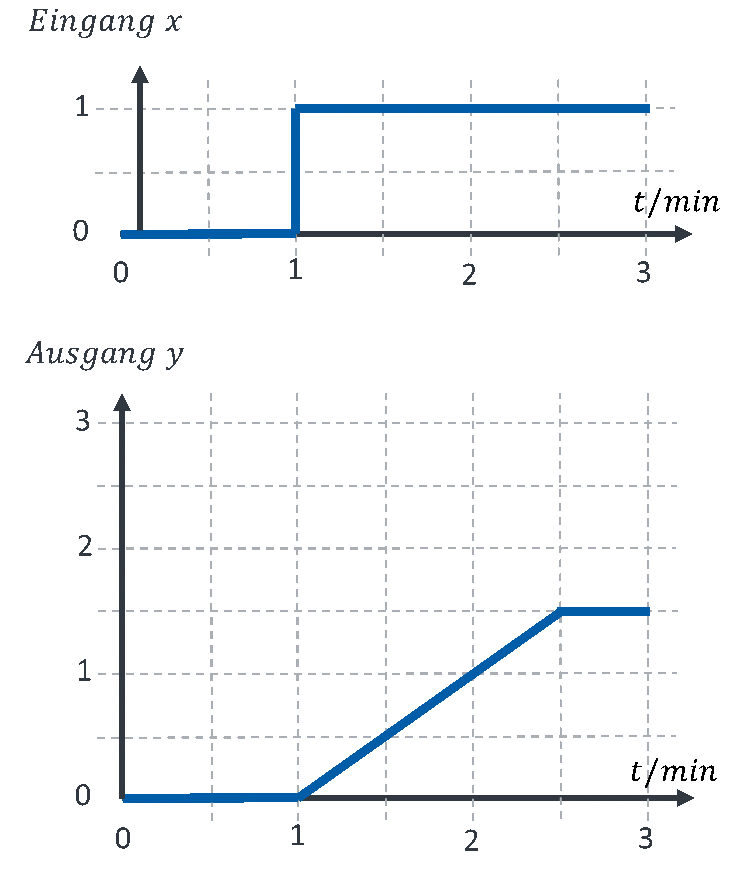
Sie sollten ein System immer in einem Bereich betreiben, in dem der Ausgleich noch nicht wirkt. Sonst bekommen Sie ein Verhalten, das Sie vorher so nicht berechnet hatten. Achten Sie darauf, dass im Übertragenen Sinn der Eimer nie überläuft oder leerläuft.
Weiter