Ein Mikrocontroller arbeitet Befehle sequentiell ab. Er bekommt Daten von einem AD-Wandler sequentiell zur Verfügung gestellt. Eine Filterung im Mikrocontroller erfolgt also fortlaufend, während ständig neue Messdaten vom AD-Wandler bereitgestellt werden. Wir erzeugen schrittweise einen Quellcode, der gefilterte Ausgangsdaten immer dann bereitstellt, wenn ein neuer Wert am ADC als Eingangsgröße verfügbar ist.
Zur Herleitung einer einfachen Filterfunktion betrachten wir ein analoges Tiefpassfilter aus Widerstand und Kondensator:
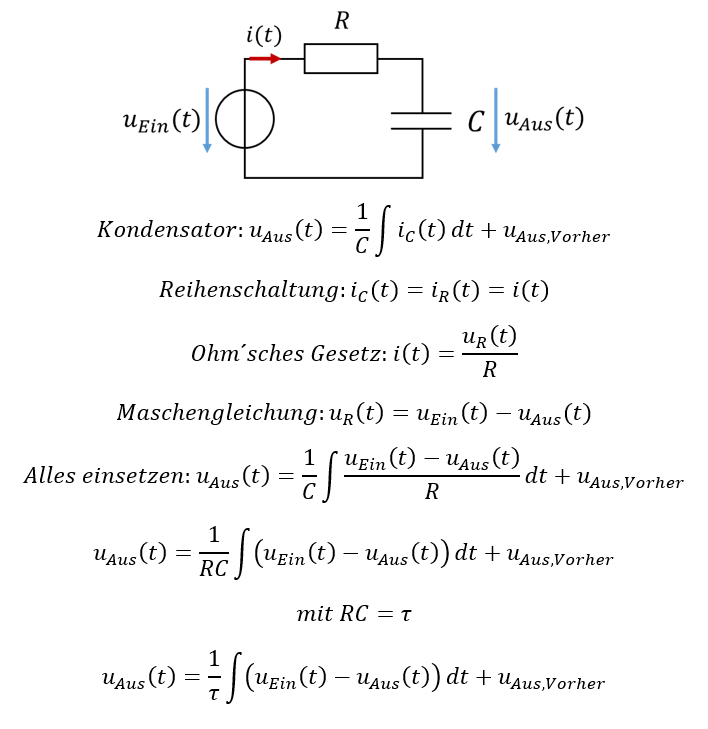
Wir betrachten diese Gleichung jetzt in zeitdiskreten Schritten der Länge Δt. Sobald dieses Zeitintervall vergangen ist, liegt ein neuer Wert am Ausgang des ADCs vor. Dieser neue Wert wird als Eingangsgröße zum digitalen Filter hinzugefügt. Wir betrachten eine aktuelle Ausgangsspannung und eine aktuelle Eingangsspannung zum Zeitpunkt n. Einen Zeitschritt Δt später haben wir den Zeitpunkt n+1.
Wir betrachten die Änderung der Ausgangsspannung über ein solches Zeitintervall Δt. Zum Zeitpunkt n+1 gilt auf Basis der Werte zum Zeitpunkt n:
Die Eingangsspannung uEin(t) wird im Quellcode durch eine Eingangszahl zEin(n) aus dem ADC ersetzt. Das Integral über der Ausgangsspannung uAus(t) dt wird zu einer Ausgangszahl zAus(n) ∙ Δt. Zum Zeitpunkt n lag die Ausgangsspannung uAus,Vorher am Kondensator an. Dies entspricht der Ausgangszahl des Rechenschritts vor der Integration zAus(n).
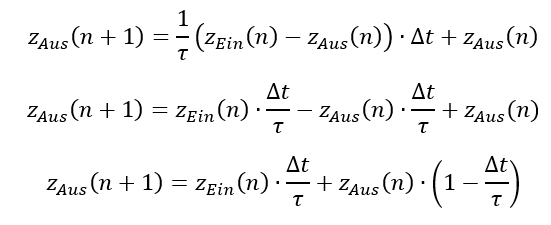
Interpretieren wir die letzte Zeile. Da steht, dass die neu vom ADC bereitgestellte Zahl zEin(n) mit dem Faktor Δt / τ gewichtet wird. Der alte Ausgangswert zAus(n) wird ebenfalls mit einem Faktor gewichtet. Anschließend werden beide Terme addiert.
Diese Rechnung wird jedes Mal ausgeführt, wenn ein neuer ADC-Wert verfügbar ist. Das Ergebnis der vorherigen Rechnung (n) geht in die neue Berechnung (n +1) mit ein.
Nehmen wir an, dass Δt viel kleiner als τ ist, z. B. Δt = τ /10. Dann wird ein 1/10 der neuen Zahl zum vorherigen Filter-Ergebnis addiert. Das Ergebnis besteht dann zu 1 – 1/10 = 9/10 aus dem vorherigen Wert. Es dauert damit einige Zeit, bis eine Änderung der Eingangszahlen sich in der gefilterten Ausgangszahl zeigt.
Nehmen wir jetzt an, dass die Eingangszahl der Ausgangszahl entspricht. Dann besteht die neue Ausgangszahl aus 1/10 der Eingangszahl plus 9/10 der identischen Ausgangszahl. Damit ändert sich die Ausgangszahl nicht, wenn die Eingangszahl der Ausgangszahl entspricht.
Ist die Eingangszahl kleiner als die Ausgangszahl, sinkt die Ausgangszahl über der Zeit. Umgekehrt steigt die Ausgangszahl, wenn die Eingangszahl größer als die Ausgangszahl ist. Sie steigt aber mit jedem Rechenschritt nur wenig an. Die Geschwindigkeit der Änderung wird vom Faktor Δt / τ bestimmt. Ein großes Tau führt zu einer langsamen Änderung, weil damit der Faktor klein wird.
Festlegen der Grenzfrequenz
Ein großes Tau ist ein Indikator für ein träges System. Das ist analog zu den Erkenntnissen aus den RC-Ladekurven (ganz hinten auf der Seite) in den Grundlagen der Elektrotechnik. Lesen Sie da bitte nochmal nach, wenn Sie das nicht direkt erkennen.
Was können wir an dem Filter beeinflussen? Δt ist die Zeit zwischen zwei Abtastungen. Die Abtastfrequenz ändern wir nicht für die Filterung, denn sie ist für die analogen Eingangssignale optimiert worden. Wir können den Parameter τ ändern. Das entspricht einer Änderung von R und C in einer analogen Filterschaltung (τ = R ∙ C).
Warum wirkt diese Formel filternd? Wir haben ein Tiefpass-Filter nachprogrammiert. Das Filter sollte also Spitzenwerte hoher Frequenzen dämpfen und die Spitzenwerte tiefer Frequenzen unverändert passieren lassen. Betrachten wir nochmal das Ergebnis der Rechnung weiter oben:
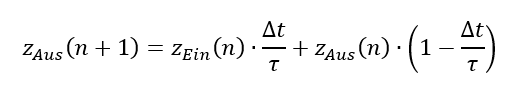
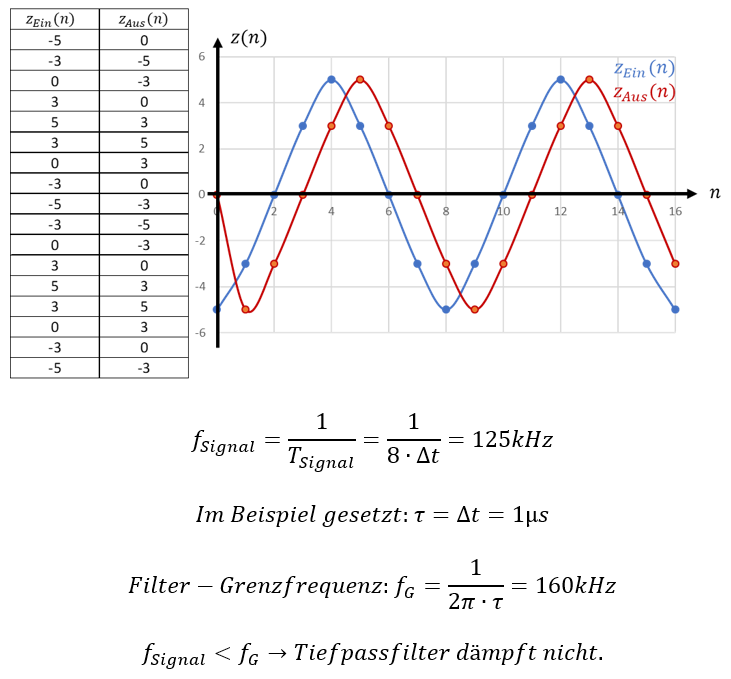
Wenden wir diese Funktion auf Beispiel-Zahlen an. Aus dem ADC kommen die Eingangszahlen in der linken Spalte. Das Ergebnis der Filterung nach der oberen Formel steht in der rechten Spalte. Ich habe für dieses Beispiel Δt = 1µs gewählt. Das entspricht einer Abtastfrequenz von 1MHz. Für die Filterwirkung habe ich τ = 10 ∙ Δt = 10µs gewählt. Bitte ignorieren Sie für dieses Beispiel, dass ein ADC keine negativen Zahlen ausgibt, es geht hier um die prinzipielle Funktion.
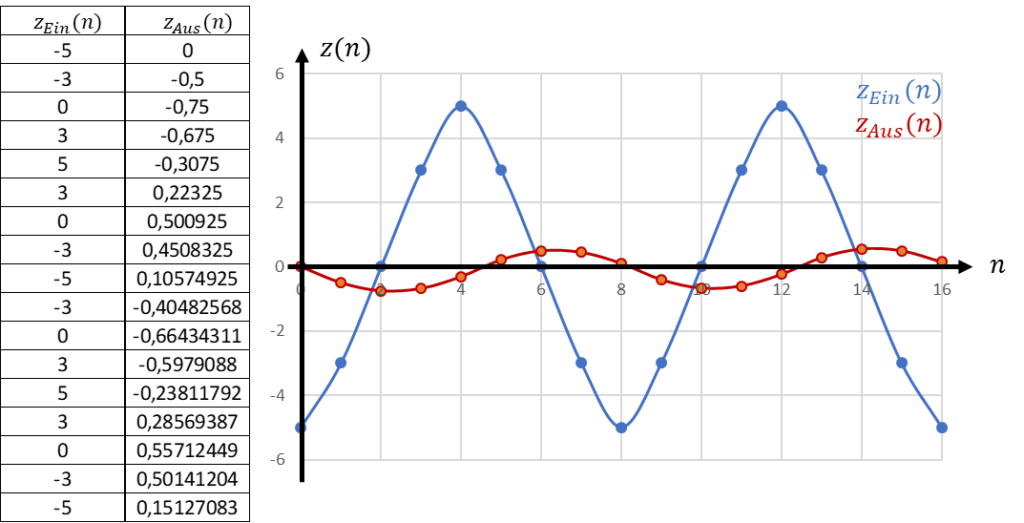
Rechts in der Abbildung sind Eingangs- und Ausgangszahlen über der Zeit gezeichnet. Die Zeit schreitet in diskreten Schritten n ∙ Δt voran. Die Punkte sind in der Grafik miteinander verbunden, damit Sie die Kurvenform besser erkennen. Im Mikrocontroller liegen nur die Zahlen vor und sie sind natürlich nicht zu einer Kurve verbunden.
Das Filter dämpft das Eingangssignal etwa um Faktor 10. Der Spitzenwert der Ausgangszahl wird reduziert und die Ausgangszahl ist phasenverschoben zur Eingangszahl. Das Signal weist die Periodendauer TSignal = 8 ∙ Δt = 8µs auf, denn es wiederholt sich nach n = 8 Werten, die alle um Δt zueinander verschoben sind. Rechnen wir nach:

Wir schieben als nächstes die Tiefpass-Grenzfrequenz im Bode-Diagramm so weit nach rechts, dass die Signalfrequenz kleiner als die Grenzfrequenz ist. Dann passiert das Signal das Filter unverändert.
Das Ausgangssignal des Filters ist im Zeitverlauf um einen Rechenschritt nach rechts verschoben. Das hat nichts mit der Phasenverschiebung des Filters zu tun, sondern mit der Berechnungsart. Sie nutzen immer vergangene Messwerte vom vorherigen Rechenschritt. Damit ist der Verlauf immer um mindestens einen Rechenschritt nach rechts verschoben.
Mittelwert-Filter
Das bisher besprochene Filter verwendet die gesamte Vergangenheit des Eingangssignals. Die alten Signalanteile werden mit dem zeitlichen Abstand zwar immer weniger stark gewichtet, aber sie sind für immer in der Rechnung enthalten. Das tut ein analoges Filter auch. Wir können auch einen gleitenden Mittelwert für das Filter nutzen. Dieser nutzt ein fest definiertes Zeitfenster. Es gilt:
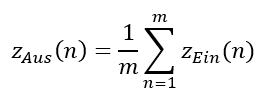
Dieses Filter verwendet immer eine feste Anzahl m an Eingangszahlen für die Filterung. Sobald ein neuer Wert am ADC verfügbar ist, wird er in den Mittelwert aufgenommen. Dafür wird der älteste Wert aus dem Mittelwert entfernt. Dieses Filter wirkt ähnlich.
Überlegen Sie mal, wie Sie dieses Filter mit möglichst wenig Rechenoperationen in C-Code realisieren können.
Weiter