Betrachten wir die Sprungantwort eines Funktionsblocks oder eines charakteristischen Systems. Im letzten Kapiteln haben wir besprochen, dass es zwei charakteristische Zeitpunkte gibt, bei denen die Systemberechnung einfach ist: Nach unendlich langer Zeit ist das System nach dem Sprung eingeschwungen. Die Ausgangsgröße ändert sich über der Zeit nicht mehr. Wir berechnen dieses Verhalten, indem wir s = 0 in die Übertragungsfunktion einsetzen. Dadurch wird die Übertragungsfunktion i. A. deutlich vereinfacht.
Der zweite Punkt ist der Sprungzeitpunkt. Hier gilt s → ∞. Auch dieser Wert von s ist i. A. einfach zu berechnen. Betrachten wir dazu nochmal PT-1-Verhalten:
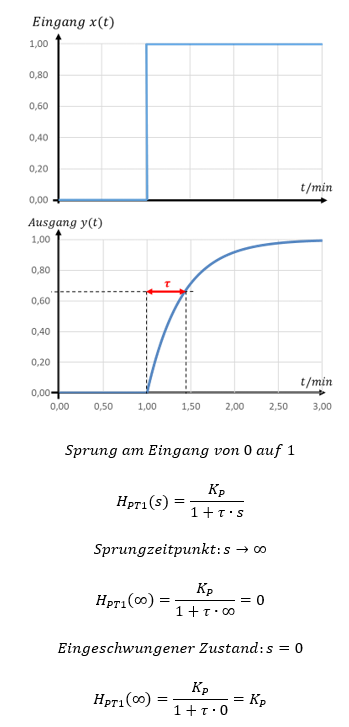
Wir betrachten den Zwischenbereich nicht mathematisch, sondern nur phänomenologisch. Wir berechnen also nichts, sondern betrachten den Übergangsbereich zwischen den beiden Zuständen nur grob. Die Berechnung des Übergangsbereichs überlasse ich gerne Matlab, sowas macht man nicht von Hand.
Die Qualität eines Regelkreises wird am Sprungzeitpunkt, im Übergangsbereich und im eingeschwungenen Zustand bewertet. Wir vergleichen an den drei Stellen die Verhaltensweisen P und I in einem Regelkreis. Dazu geben wir A einmal nur P-Verhalten und einmal I-Verhalten:
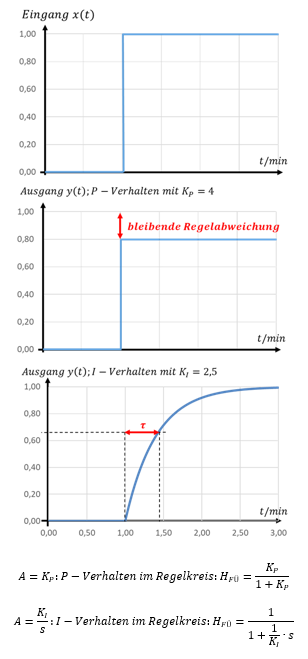
Sprungzeitpunkt
Der Sprungzeitpunkt gibt an, wie der Regelkreis unmittelbar auf Änderungen reagiert. P-Verhalten reagiert sofort. I-Verhalten reagiert verzögert. Das können wir aus den Sprungantworten direkt ablesen.

Der Regelkreis mit I-Verhalten reagiert zum Sprungzeitpunkt noch überhaupt nicht (H = 0). Der Regelkreis mit P-Verhalten springt direkt auf seinen Endwert (H = 0,8).
Übergangsverhalten
P-Verhalten kennt kein Übergangsverhalten, weil es nicht verzögernd wirkt. Das Übergangsverhalten von I-Verhalten wird durch den Parameter τ beschrieben. Je kleiner τ ist, desto schneller erreicht die Ausgangsgröße ihren Endwert.
Eingeschwungener Zustand
Im eingeschwungenen Zustand weist P-Verhalten eine bleibende Regelabweichung auf. Der Ausgang beträgt y = 0,8 statt y = 1 bei KP = 4. I-Verhalten dagegen weist keine bleibende Regelabweichung auf. Der Ausgang erreicht bei I-Verhalten den Sollwert 1 vollständig.

Warum weist I-Verhalten keine bleibende Regelabweichung auf? Vergleichen wir dafür nochmal den Regelkreis mit P-Verhalten und mit I-Verhalten:
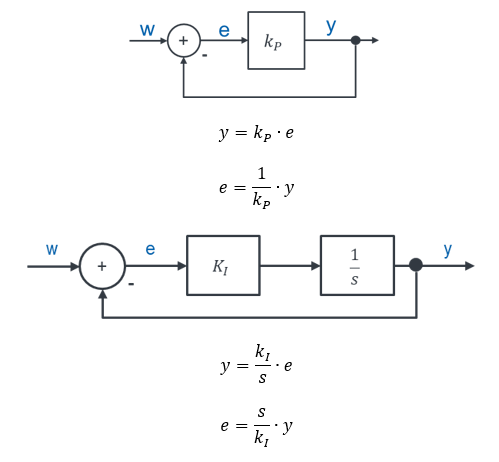
In einem geregelten System mit P-Verhalten gilt für e = 0 immer y = 0. Deshalb muss es eine Regelabweichung e geben, wenn das System am Ausgang einen Wert ungleich 0 aufweist. Speicher haben die Eigenschaft, dass ihr Ausgang seinen Wert konstant hält, wenn der Eingang den Wert 0 aufweist. Mit einem Speicher können wir also erreichen, dass e = 0 gilt bei y > 0. Wie geht das mathematisch?
Für HFü = 1 brauchen wir A → ∞. Bei einem System mit P-Verhalten muss die Verstärkung kP also sehr groß sein, damit die Regelabweichung e klein wird. Beim Integrieren wird die Ausgangsgröße über der Zeit immer größer. Bei einem System mit I-Verhalten können wir stattdessen also auch eine lange Zeit t lang warten.
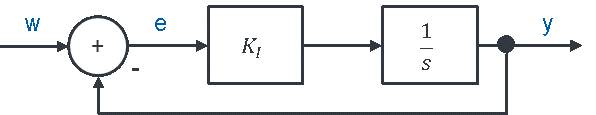
Angenommen beim oberen Regelkreis mit I-Verhalten gilt w = 1 und y = 0. Dann haben wir e = w – y = 1. Das ist der Zulauf zum Speicher. Der Füllstand y steigt über der Zeit an. Nach einiger Zeit ist w = 1 und y = 0,5. Jetzt beträgt e nur noch 0,5. Der Zulauf zum Speicher ist geringer und der Füllstand y steigt langsamer an. Aber er steigt noch an, so dass etwas später y = 0,9 gilt. Damit gilt e = 1 – 0,9 = 0,1. Die Regelabweichung e ist jetzt noch kleiner, so dass der Speicher immer langsamer gefüllt wird.
Über der Zeit t sinkt die Regelabweichung e immer weiter, und der Füllstand des Speichers y erreicht immer besser den Sollwert w = 1. Nach längerer Zeit ist die Regelabweichung kleiner als unsere Messmöglichkeiten. Wir haben den eingeschwungenen Zustand erreicht. Damit lässt sich der PT-1-förmige Einschwingvorgang des geregelten Systems mit I-Verhalten erklären.
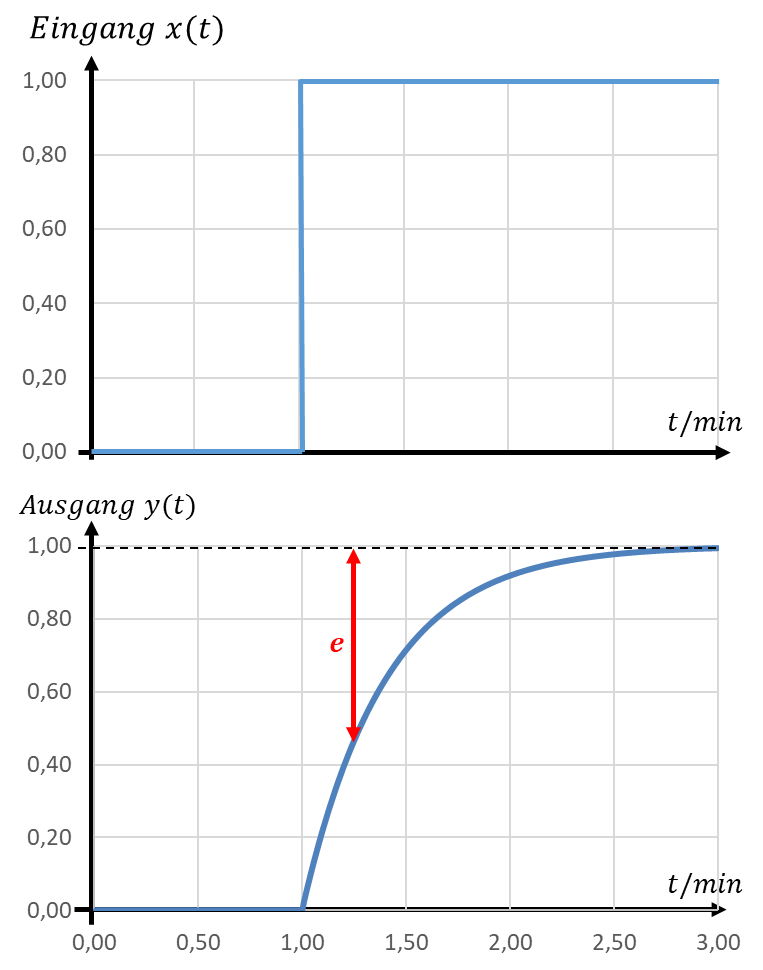
Die Regelabweichung e wird in der Grafik als Differenz zwischen der Linie y = 1 und dem Verlauf von y(t) dargestellt. Das gilt natürlich erst nach dem Sprung ab t ≥ 1s. Es wird deutlich, dass e über der Zeit sinkt und y sich immer besser dem Sollwert annähert.
Weiter