Viele physikalische Größen wirken auf ohm´sche Widerstände. Deshalb wird in diesem Kapitel besprochen, wie eine Widerstandsänderung in einer Spannungsänderung umgewandelt werden kann. Dazu betrachten wir einen PT100-Widerstand mit folgender Kennlinie aus Widerstandswert über der Temperatur:
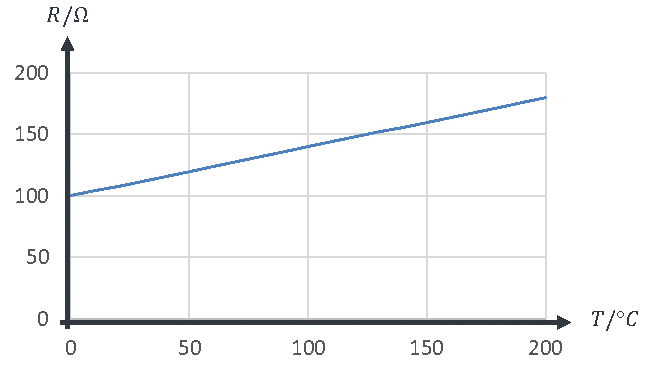
Der Verlauf der Kennlinie ist leicht nichtlinear. Das kann man in der Grafik kaum sehen. Er kann rund um den Wert T = 0°C herum durch eine Näherung linearisiert werden:
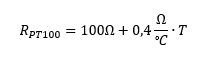
Bei einer Temperatur von T = 0°C weist der Sensor den Widerstand RPT100 = 100Ω auf. Dieser Punkt ist namensgebend. Bei Erhöhung der Temperatur steigt der Widerstandswert nahezu linear an. Wir können den Widerstandswert in einen festen Widerstandswert und einen temperaturabhängigen veränderlichen Widerstandswert aufteilen:
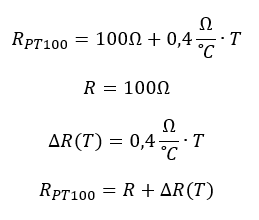
Die Aufteilung eines Messwiderstands in einen unveränderlichen Teil R und einen von der physikalischen Größe abhängigen Teil ΔR ist für die weiteren Kapitel sehr wichtig. Im Beispiel oben ist der unveränderliche Teil R = 100Ω und der veränderliche Teil ΔR=0,4Ω/°C ·T. Um diese Aufteilung zu üben gebe ich Ihnen ein weiteres Beispiel für einen (ausgedachten) Drucksensor:
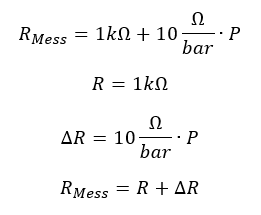
Eine Widerstandsänderung kann nicht in eine digitale Zahl umgewandelt werden, sie kann also nicht digitalisiert werden. Es können nur Spannungen digitalisiert werden. Die Digitalisierung von Strömen und Zeiten ist so selten, dass ich sie hier nicht behandle. Deshalb muss der Widerstandswert des Sensors in einen Spannungswert umgewandelt werden. Es werden drei Möglichkeiten dazu verglichen. Sie sollen dabei lernen, wie Lösungen anhand von Kriterien bewertet werden können.
Folgende Kriterien werden angesetzt:
1. Die Kennlinie soll möglichst proportional sein.
2. Der Aufwand für die Realisierung soll gering sein.
3. Es soll eine möglichst hohe Sensitivität erreicht werden. Die Spannung soll sich bereits bei einer geringen Temperaturänderung möglichst stark ändern.
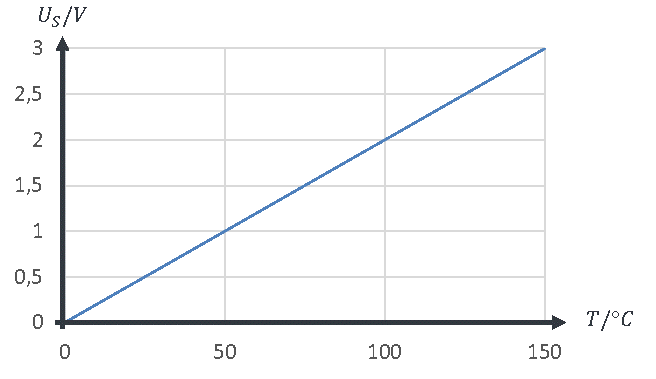
Was wir als Ideal erreichen wollen sieht grafisch folgendermaßen aus: