Vielleicht haben Sie schon einmal ein Kind auf einer Schaukel angeschoben. Oder Sie haben auf einer Schaukel gesessen. Sie werden festgestellt haben, dass die Frequenz der Schwingung der Schaukel sich nicht ändert, egal was Sie tun. Sie können noch so fest anschieben, Sie können der Schaukel einen heftigen Impuls geben … die Schaukel schwingt immer mit der gleichen Frequenz. Sie ändern nur die Höhe der Endlage, also den Spitzenwert.
Jedes schwingfähige System hat eine „Resonanzfrequenz“, bei der es schwingen kann. Sie können die Resonanzfrequenz der Schaukel konstruktiv ändern, indem Sie die Länge der Seile der Schaukel verändern. Bei längeren Seilen sinkt die Schwingfrequenz. Ist die Schaukel einmal aufgehängt, können Sie diese aber nicht mehr ändern. Sie ist auch nicht vom Gewicht auf der Schaukel abhängig.
Die Resonanzfrequenz eines Systems ergibt sich aus den physikalischen Gleichungen. Dafür stellen wir die Differenzialgleichung der Bewegung auf. Wir haben bisher mit den Richtungen x und y gearbeitet, um beide Energieformen zu beschreiben. Jetzt stellen wir mit einem mathematischen Trick beide Energieformen nur noch in Abhängigkeit von x dar und setzen sie gleich. Wir betrachten dafür das ausgelenkte Pendel als Dreieck.
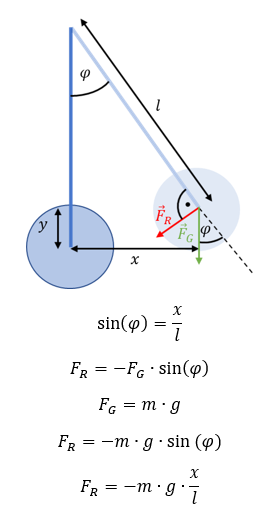
Ein Anteil der Schwerkraft FG hält den Faden des Pendels gespannt. Er wirkt in Richtung des Fadens nach unten rechts. Ein anderer Teil der Schwerkraft ist die Rückstellkraft FR. Sie wirkt in Richtung der Pendelbewegung. Das Vorzeichen der Kraft ist negativ, denn sie wirkt in Richtung -x. Wir können diese Kraft aus den Größen Pendelmasse m, Gravitationskonstante g, Auslenkung x und Fadenlänge l berechnen.
Für die Kraft einer Bewegung gilt:
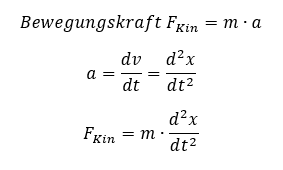
Wir vereinfachen dabei wieder, dass die Bewegung nur in x-Richtung erfolgt. Die Berechnung gilt also nur für Pendel, die relativ zur Fadenlänge l um so wenig x ausgelenkt werden, dass der y-Anteil der Bewegung vernachlässigt werden kann.
Wir setzen jetzt die Kräfte gleich. Es gilt:
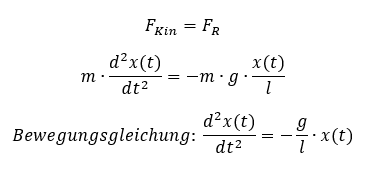
Es können nur Bewegungen existieren, die die unterste Gleichung erfüllen. Die Gleichung gilt für den Fall, dass keine Energie von außen zu- oder abgeführt wird. Um zu prüfen, ob das Pendel eine bestimmte Art von Bewegung „von selbst“ ausführen kann, setzen wir die mathematische Beschreibung der Bewegung in diese Gleichung ein. Wenn es eine Lösung der Gleichung mit der Bewegungsform gibt, ist die Bewegung möglich.
Die Gleichung ist für x(t) = 0 erfüllt. Das ist das Pendel in der Ruhelage. Dieser Betriebspunkt ist zwar mathematisch richtig, er ist aber für die Beurteilung einer Schwingung nicht hilfreich.
Einschub: Wir können auch andere Bewegungsarten ausprobieren, z. B. eine lineare Bewegung.

Die Gleichung hat für eine lineare Bewegung nur eine Lösung für x = 0 bei t = 0. Das ist der Stillstand. Also kann es keine lineare Bewegung eines Pendels geben, denn eine Bewegung braucht andere x-Werte als 0. Der Punkt x = 0 oder die Zeit t = 0 lösen die Gleichung immer für alle Bewegungsarten.
Mit diesem Einschub wollte ich Ihnen nur einmal zeigen, welche Bewegung nicht möglich ist. Wenn Sie das jetzt noch nicht verstehen, ist das nicht schlimm. Im nächsten Abschnitt folgt eine physikalisch mögliche Bewegung. Im Vergleich der Bewegungsfunktionen sollte klar werden, welche möglich ist und warum.
Probieren wir was anderes: Wir wissen bereits, dass die Bewegung in x-Richtung sinusförmig verläuft. Deshalb setzen wir einen Sinus ein und schauen, ob die Gleichung erfüllt wird. Um kompatibel zur Literatur zu bleiben, setze ich einen Cosinus statt eines Sinus ein. Das ändert nur die Phasenlage. Wir lassen das Pendel jetzt in einer Endlage los. Damit starten wir mit einem maximalen positiven Wert von x und wir haben eine cosinus-förmige Bewegung.
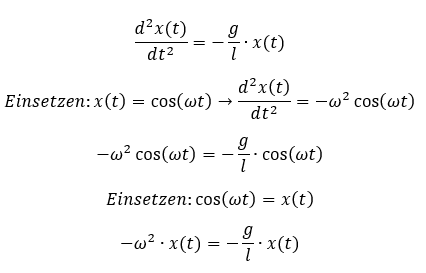
Wir können den Term x(t) kürzen, dann wird die Gleichung einfacher:
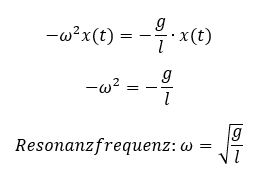
Für eine Bewegung müssen beide Seiten der Gleichung gleich groß sein. Auf beiden Seiten der Gleichung steht der Term x(t). Diese Terme x(t) sind schon mal auf beiden Seiten der Gleichung gleich groß. Die restlichen Terme ergeben eine Anforderung an ω. Bei einer Bewegung mit x(t) = cos(ωt) zwingt die Gleichung ω einen festen Wert auf – die Resonanzfrequenz.
Die Gleichung weist für alle x eine Lösung auf, wenn wir als Bewegungsform einen Sinus oder Cosinus einsetzen. Eine sinusförmige Bewegung ist für ein Pendel also mit jedem x-Wert möglich. Vergleichen wir diese Lösung mit der linearen Bewegung: Da gab es nur eine Lösung für die Bewegungsgleichung bei x = 0. Das ist der Startpunkt der linearen Bewegung und entspricht dem Verharren in der Ruhelage. Das Pendel kann also nur entweder sinusförmig schwingen oder in seiner Ruhelage verharren.
Das Pendel schwingt immer sinusförmig bei der Resonanzfrequenz, die aus Gravitationskonstante und Fadenlänge bestimmt wird. Bei einer anderen Kreisfrequenz wird die Bewegungsgleichung nicht erfüllt. Also kann das Pendel immer nur bei der gleichen Frequenz schwingen. Das deckt sich auch mit der praktischen Erfahrung mit Pendeln.
Sobald äußere Kräfte hinzugefügt werden, kann das Pendel jede andere Form der Bewegung ausführen. Wenn Sie das Pendel z. B. mit der Hand anhalten oder anstoßen, dann gilt die Bewegungsgleichung nicht mehr, die nur für zwei innere Kräfte aufgestellt worden ist.
Interessanterweise ist die Resonanzfrequenz, bei der das Pendel schwingt, nur von der Fadenlänge und nicht etwa vom Gewicht abhängig. Das können wir erst erkennen, wenn wir die Kraftgleichung aus der Physik aufgestellt haben. Bei jedem schwingfähigen System gibt es andere Bewegungsgleichungen bzw. Systemgleichungen, die die Physik der Systeme abbildet. Die meisten sind nicht so einfach wie die des Pendels, deshalb betrachte ich sie hier nicht weiter.
Weiter