Stellen Sie sich ein Signal vor, das aus mehreren sinusförmigen Verläufen unterschiedlicher Frequenzen besteht. Als Beispiel nehmen wir ein Signal mit einem Anteil mit hoher Frequenz und geringerer Amplitude und einem Anteil mit niedriger Frequenz und höherer Amplitude. Wie so ein Signal zustande kommt siehe Messtechnik Filter.
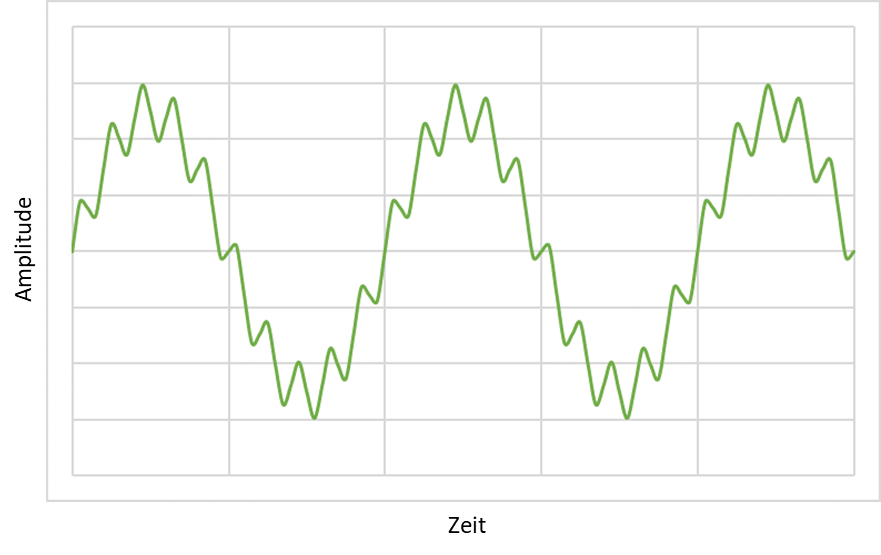
Die Aufgabe besteht darin, Spitzenwert, Phase und Frequenz der einzelnen Signalanteile zu ermitteln. Angenommen, dieses Signal liegt am Ausgang des Sensors als Spannungssignal vor. Sie haben in Messtechnik gelernt, wie Sie dann so ein Signal analog verstärken, verschieben und filtern können, damit es optimal auf den Eingangsspannungsbereich eines ADCs passt. Im ADC wird das Signal digitalisiert und es liegt am Ausgang als Zahlenstrom vor. Der ADC gibt in festen Zeitabständen Zahlen aus, die z. B. von einem Mikrocontroller in einen Speicher geschrieben werden.
Um die Aufgabe zu vereinfachen, betrachten wir zunächst nur ein einziges sinusförmiges Signal. Eine Periode eines sinusförmigen Signals mit 20 Abtastpunkten könnte folgendermaßen aussehen, wenn es von einem 8 Bit ADC digitalisiert worden ist:

Die Zahlenwerte liegen im Bereich [0 .. 255]. Es handelt sich um ein zeitdiskretes und wertediskretes Signal. Das Signal in der oberen Abbildung weist z. B. die Frequenz 1kHz auf und es wurde mit 20 KSPS (fAbtast = 20kHz) abgetastet.
Wird bei einem zeitkontinuierlichen Signal die Zeit t kontinuierlich erhöht, entspricht das bei einem zeitdiskreten Signal einem Sprung von einem Abtastwert zum nächsten. Wir starten die Betrachtung an Wert 255 an Speicherstelle 5. Wenn jetzt das Signal zu einer etwas späteren Zeit betrachtet wird, nehmen wir den Wert von Speicherstelle 6 (249). Statt einem Spannungsverlauf U(t) sprechen wir jetzt von einem Zahlenverlauf Zahl(n). Der Laufindex n gibt dabei an, an welcher Stelle im Speicher wir gerade von der zeitlichen Abfolge her sind. Zwischen den „Zeiten“ n und n + 1 liegt die Periodendauer der Abtastfrequenz:
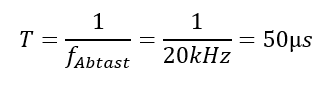
Aus der Zahlenfolge im Speicher kann nicht rekonstruiert werden, in welchem Zeitabstand die Daten abgetastet worden sind. Da Sie aber wissen, mit welcher Abtastfrequenz der von Ihnen ausgewählte ADC arbeitet, wissen Sie, wie lang die Zeit zwischen zwei Datenpunkten im Datenstrom war.
Bei sinusförmigen Signalen interessieren oft die Parameter, die das Signal mathematisch beschreiben: Spitzenwert, Frequenz und Phase.
Den Spitzenwert könnten Sie ermitteln, indem Sie das Maximum und das Minimum des Signals im Datenstrom suchen. Dafür gibt es fertige Algorithmen.
Die Periodendauer – und daraus die Frequenz – können Sie ermitteln, indem Sie die Nulldurchgänge des Signals erfassen. Die Zeit zwischen zwei Nulldurchgängen entspricht der halben Periodendauer des Signals. Wenn Sie die Anzahl der Abtastpunkte zwischen zwei Nulldurchgängen zählen (im Beispiel oben 10), und Sie wissen, dass diese Zeit 10 Periodendauern der Abtastfrequenz von jeweils 50 µs entspricht. Die Periodendauer des Signals ist also TSignal = 20 ∙ TAbtast = 20 ∙ 50µs = 1 ms lang. Daraus ergibt sich die Frequenz fSignal = 1 / TSignal = 1 kHz.
Die Phase kann nur bestimmt werden, wenn es irgendeinen Bezug gibt. Wenn z. B. zwei Signale betrachtet werden, dann kann die Phase aus der der zeitlichen Verschiebung der Signale zueinander bestimmt werden. Oder betrachten wir Strom- und Spannungssignal aus dem Kapitel Leitfähigkeitsmessung . Wenn diese Signale zueinander zeitlich verschoben sind, dann können wir eine Phasenverschiebung zwischen den Signalen angeben. Die Phase bezieht die Zeitverschiebung auf die Periodendauer. Sie gibt diese also nicht in Sekunden an, sondern quasi in Prozent der Periodendauer (nur nicht bezogen auf 100 wie bei Prozent, sondern bezogen auf 360° oder 2π) an.
Die vorgestellten Methoden der Signalverarbeitung haben den Nachteil, dass sie schnell an ihre Grenzen gelangen. Schauen Sie sich die erste Grafik auf dieser Seite noch einmal an. Versuchen Sie einmal, die Maxima und Minima oder die Nulldurchgänge beider Signale getrennt voneinander aus dem Signalverlauf zu ermitteln. Das geht bei Überlagerung mehrerer Signale nicht mehr. Deshalb arbeiten wir nicht länger im Zeitbereich, sondern ab jetzt im Frequenzbereich.
Weiter.