Die Wirkung eines Kondensators als Speicher soll an einem Beispiel veranschaulicht werden. Sie können die zugehörige Schaltung als optionalen Versuch im Praktikum aufbauen. Die Parameter der Schaltung sind nicht ganz realistisch, weil sie mit Bauelementen, die im Praktikum verfügbar sind, realisiert werden sollen. Dieser Teil des Tutorials ist optional, Sie brauchen ihn nicht für die Klausur vollständig zu verstehen.
Eine batteriebetriebene Schaltung soll kontinuierlich eine Temperatur messen und den Messwert einmal pro Sekunde über ein Funkmodul an ein Smartphone senden. Auf dem Smartphone läuft eine App, auf der der Temperaturwert angezeigt wird. Für die Schaltung benötigen wir eine Batterie, ein elektronisches Thermometer und ein Funkmodul. Diese Komponenten werden zunächst modelliert.
Modellierung
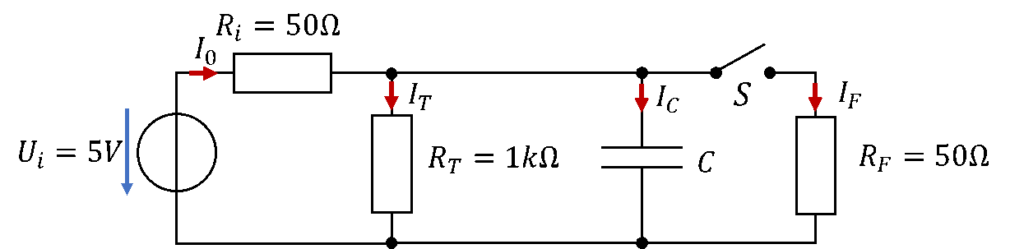
Als Batterie verwenden wir einen Akku als reale Spannungsquelle. Er weist eine Leerlaufspannung von Ui = 5V und einen Innenwiderstand von Ri = 50Ω auf. Das sind zwar keine realistischen Werte für einen Akku, aber damit zeigt sich gut das Verhalten einer realen Spannungsquelle. Folgendes Schaltbild zeigt die Modellierung des Akkus:
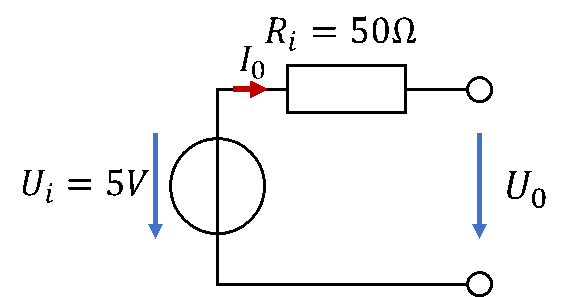
Das elektronische Thermometer benötigt bei 5V Betriebsspannung einen Strom von 5mA. Es wird als Widerstand modelliert. Das bedeutet, dass für Berechnung und Modellierung der Zusammenhang zwischen Spannung und Strom am Thermometer mit dem Ohm´schen Gesetz berechnet wird. Es ist kein Widerstand, es hat einen Widerstandswert als Eigenschaft.
Das Thermometer wird direkt an die Anschlussklemmen der realen Batterie angeschlossen. Es ist damit in Reihe zum Innenwiderstand des Akkus versschaltet.
Das Funkmodul benötigt für eine Übertragung von 1ms Dauer bei 5V ein Strom von 100mA. Wir modellieren das Funkmodul ebenfalls als Widerstand.
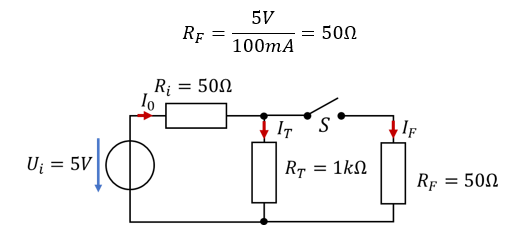
Das Funkmodul ist nicht dauerhaft aktiv, es ist nur einmal pro Sekunde für die Dauer von 1ms eingeschaltet. Wir schalten das Funkmodul deshalb hinter einen Schalter S. Es wird parallel zum Thermometer verschaltet, damit es die gleiche Spannung von 5V direkt aus dem Akku bekommt. Funkmodul und Thermometer benötigen beide eine Mindestspannung von 4V für den Betrieb.
Berechnung
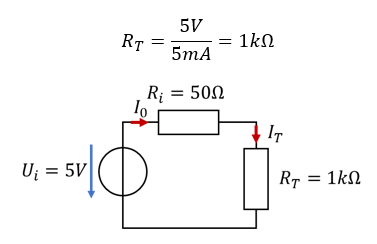
Immer wenn der Schalter S offen ist, liegt ein Spannungsteiler aus Ri und RT vor. Die Spannung an RT beträgt dann:
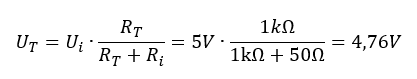
Die Spannung am Thermometer ist etwas kleiner als die innere Spannung der realen Spannungsquelle, weil Strom aus der Quelle fließt. Je weniger Strom herausfließt, desto höher ist die Ausgangsspannung des Akkus.
Immer wenn der Schalter S geschlossen ist, liegt eine Parallelschaltung aus RT und RF vor. Diese können wir berechnen zu:
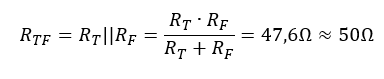
In der Parallelschaltung bestimmt der kleinere der Widerstände den Gesamtwiderstand. Die Spannung am Funkmodul berechnet sich dann aus dem Spannungsteiler
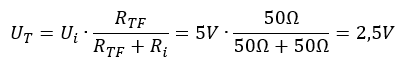
Damit ist die Spannung viel zu gering, weder das Funkmodul noch das elektronische Thermometer können mit so geringer Versorgungsspannung arbeiten. Das Funkmodul zieht so viel Strom aus der Batterie, dass die Spannung am Ausgang einbricht. Das passiert bei jeder realen Quelle ab einem gewissen Strom.
Der prinzipielle Strombedarf und der verfügbare Strom werden in folgender Grafik über der Zeit aufgetragen:
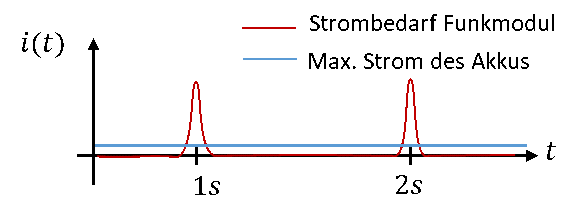
In dieser Applikation hilft ein Kondensator als Ladungsspeicher. Der Kondensator stellt kurzzeitig getrennte Ladung für das Funkmodul bereit. Er wird ständig langsam wieder aufgeladen. Er wird so platziert, dass er immer geladen und bei geschlossenem Schalter entladen wird. Wir erweitern die Schaltung folgendermaßen:
Dimensionierung des Kondensators
Um den Kondensator zu dimensionieren betrachten wir den Entladefall. Der Kondensator ist bei offenem Schalter auf etwa 5V (genauer 4,76V) aufgeladen. Wir schätzen den Wert mit gerundeten Zahlenwerten ab. Er darf maximal auf 4V entladen werden. Die Spannung am Kondensator darf also während der Übertragung der Temperatur durch das Funkmodul nur um maximal ΔU = 1V sinken. Der Strom aus dem Kondensator beträgt I = 100mA, der über die Zeit t = 1ms fließt.
Wir tun so, als sei der der Strom in das Funkmodul während der Zeit, in der der Schalter geschlossen ist, konstant. Das ist auch die Zeit, über die wir beim Entladevorgang integrieren. Diese Annahme stimmt allerdings nur, wenn die Spannung am Funkmodul auch konstant ist. Das Funkmodul wird ja als Widerstand modelliert.
Diese Annahme stimmt also eigentlich nicht. Wir nutzen sie dennoch, sonst müssten wir ja die Stammfunktion des Integrals lösen. Weil wir das umgehen wollen nehmen wir den Strom als konstant an und machen damit bewusst einen Fehler. Am Ende schauen wir nach, wie schlimm der Fehler war. Ganz am Ende des Kapitels gehe ich nochmal darauf ein.
Am Kondensator gilt bei konstantem Strom:

Die Verbraucher benötigen beide mindestens 4V Spannung. Die Spannungsänderung am Kondensator darf deshalb maximal ΔU = 5V – 4V = 1V betragen. Die Gleichung zwischen Spannung und Strom ist in der letzten Zeile nach der Kapazität C aufgelöst worden. Ein Kondensator mit C = 100µF sollte genügen, damit die Spannung am Ausgang des Akkus bei geschlossenem Schalter größer als 4V bleibt.
Wir müssen den Schalter anschließend so lange offen halten, dass der Kondensator ausreichend nachgeladen wird. Ist die Nachladezeit zu kurz, ist UC0 zu klein und die Gleichung oben gilt nicht mehr. Dann genügt die Spannung an den beiden Lasten bei geschlossenem Schalter nicht mehr.
Verläufe der Lastspannung
Die Spannung an beiden Verbrauchern UT = UF ist in der folgenden Abbildung über der Zeit dargestellt. Die rote Linie zeigt an, wann der Schalter S offen oder geschlossen ist (rechte Y-Achse). Bei t=10ms schließt der Schalter S für 1ms. Der Verlauf der Spannung an der Last ist in blau bzw. grün dargestellt. Die Spannung ist auf der linken Y-Achse skaliert.
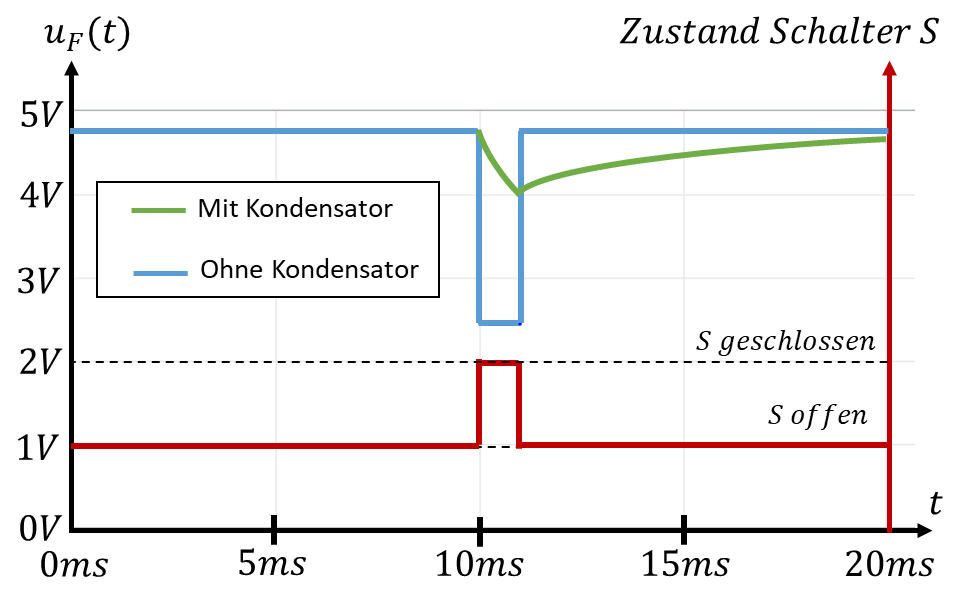
So lange der Schalter S offen ist, beträgt die Spannung an der Last 4,76V, also knapp unter 5V. Wenn der Schalter geschlossen ist, springt die Spannung an der Last ohne Einsatz des Kondensators auf die halbe Spannung, also auf 2,38V (ca. 2,5V). Wird ein Kondensator eingesetzt, sinkt die Spannung nur auf etwa 4V. Dafür muss der Kondensator anschließend wieder geladen werden. Sie erkennen ganz rechts in der Abbildung, dass dafür 10ms Zeit nicht ganz ausreichen.
Entladen und Aufladen des Kondensators erfolgen jeweils über einen Widerstand. Entladen wird er über RF und aufgeladen wird er über Ri. In beiden Fällen ändert sich die Spannung in Form einer Exponentialfunktion.
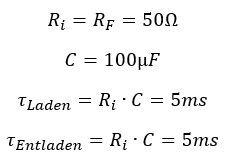
Beim Wiederaufladen erreicht die Kondensatorspannung nach τ = 5ms 63% ihres Endwerts. Da der Kondensator von 4V auf 5V aufgeladen wird, beträgt die Spannung 5ms nach Öffnen des Schalters
Nach der Zeit 5 ∙ τ = 25ms ist der Kondensator wieder auf 99% des Maximalwerts aufgeladen. Danach kann ein neuer Entladevorgang starten. Da das Funkmodul nur jede Sekunde einmal sendet ist sichergestellt, dass der Kondensator dafür jedes Mal vollständig aufgeladen ist.
Betrachten wir den Entladevorgang. Der Kondensator wird vom Funkmodul von 4,76V auf 2,38V entladen. Warum das? Nach Abschluss des Lade- bzw. Entladevorgangs fließt kein Strom mehr am Kondensator. Wenn kein Strom aus dem Kondensator fließt, dann wirkt er in der Schaltung nicht. Spannung und Strom in einer Schaltung nach vollständig abgeschlossenem Lade- oder Entladevorgang erhalten wir, indem wir den Kondensator gedanklich aus der Schaltung entfernen. Die Spannung an der Last fällt also am Ende des Entladevorgangs auf den Wert, auf den die hellblaue Spannungskurve fällt.
Das dauert etwa die Zeit t = 5 ∙ τ = 15ms. Danach wäre er um 99% entladen bzw. teilentladen. Der Entladevorgang wird aber nach 1ms schon wieder abgebrochen, deshalb sinkt die Spannung nicht bis auf 2,38V.
Um den Entladevorgang besser verstehen zu können brechen wir ihn nicht nach 1ms ab. Zum Zeitpunkt t = 15ms ist in der Abbildung unten die Kondensatorspannung um 63% gefallen.
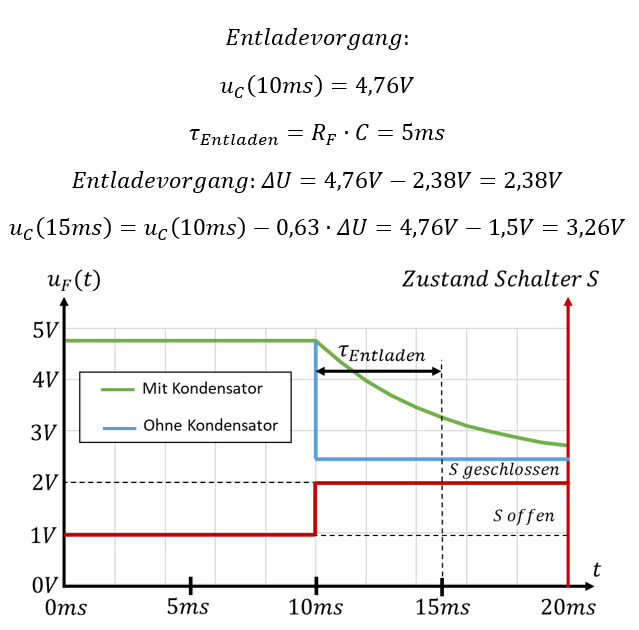
Die Herausforderung liegt darin zu erkennen, von welchem Startwert sich die Spannung auf welchen Endwert verändert. Die 63% beziehen sich immer auf die Spannungsdifferenz ΔU zwischen Start- und Endwert. Hier kann man leicht mit den Vorzeichen durcheinanderkommen. Das ist unkritisch, denn Sie wissen ja, ob die Spannung steigt oder fällt. Die Vorzeichen der Berechnung können Sie (auch in der Klausur) am Ende korrigieren, wenn Sie diese in den Formeln falsch angesetzt hatten.
Der Entladevorgang aus der zweiten Grafik tritt in der Praxis nicht auf, denn das Entladen wird immer nach 1ms abgebrochen. Dann ist der Temperaturwert bereits zum Smartphone gesendet worden. Die zweite Grafik dient nur der Veranschaulichung des Entladevorgangs.
Wir haben bei der Berechnung der Kondensatorgröße angenommen, dass der Entladestrom während des Entladevorgangs konstant ist. Das ist er nicht, denn die Spannung am Lastwiderstand sinkt über der Zeit (grüne Kurve). Mit dieser falschen Annahme haben wir die Kapazität auf C = 100µF dimensioniert. Mit der Kapazität sind die oberen Kurven simuliert worden. Die Simulation rechnet die Differenzialgleichungen aus und liefert das mathematisch exakte Ergebnis. Unsere Näherung war also offensichtlich OK, denn die Spannung an den Verbrauchern bleibt größer als 4V, wenn der Schalter 1ms lang geschlossen wird.
Weiter