Das Filter wird durch seine Grenzfrequenz charakterisiert. Bisher haben wir diese als festen Wert angenommen und geprüft, wie Signale vom Filter verändert werden. In der Praxis ist das Vorgehen genau anders herum. Sie haben Signale vorliegen und wollen diese mit einem speziellen Filter beeinflussen.
Das Nutzsignal soll das Filter unverändert passieren. Wir wollen eine möglichst hohe Reduktion des Spitzenwerts des Signals von Störungen. Bauen wir dazu ein passendes Filter auf. Wie muss die Grenzfrequenz des Filters gewählt werden, damit beide Bedingungen optimal erfüllt werden? Dafür betrachten wir zunächst ein Beispiel, um daraus das allgemeine Verfahren abzuleiten.
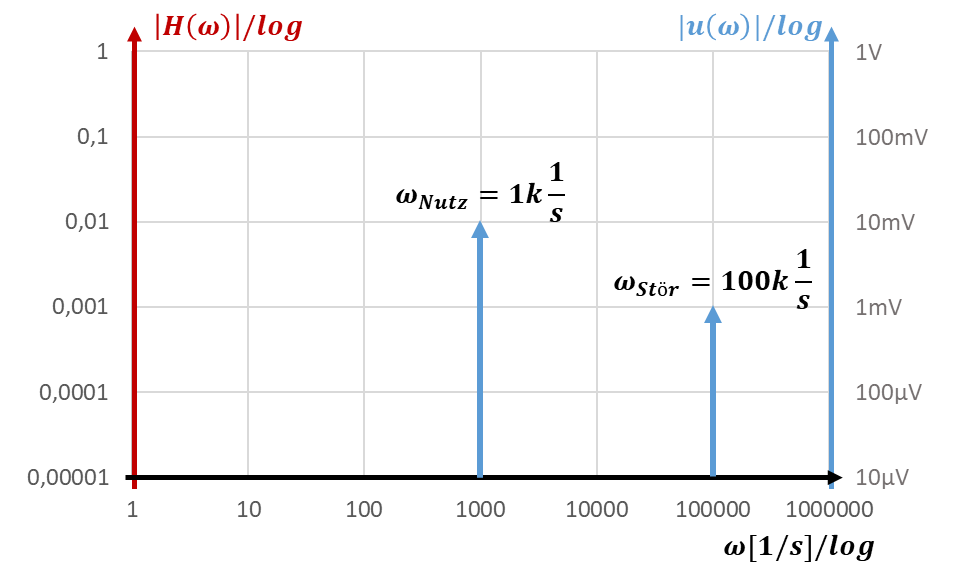
Im oberen Bode-Diagramm sehen Sie links eine y-Achse für die Übertragungsfunktion |H(ω)| in rot. Rechts sehen Sie eine weitere y-Achse in blau für Spannungen. Wir bilden in einem Diagramm Spitzenwerte von Signalspannungen (blau) und eine Filter-Übertragungsfunktion (rot) ab. Im ersten Schritt betrachten wir nur die Spannungen. Ein Nutzsignal mit Spitzenwert 10mV und Kreisfrequenz ωNutz = 1k 1/s wird durch den mittleren Pfeil dargestellt. Ein Störsignal mit Spitzenwert 1mV und Kreisfrequenz ωStör = 100k 1/s wird durch den rechten Pfeil dargestellt.
Die Signale sind eigentlich Punkte und keine Pfeile. Die Spitze der Pfeile weist auf die Punkte, die die Spitzenwerte der Spannungen auf der rechten Achse darstellen.
Wir legen als nächstes eine Übertragungsfunktion |H(ω)| in rot in das Diagramm hinein, so dass das Filter das Nutzsignal mit |H(ωNutz)| = 1 unverändert passieren lässt. Weil das Filter an der Eckfrequenz bereits die Verstärkung |H| ≈ 0,7 aufweist, legen wir die Grenzfrequenz des Filters immer mindestens um Faktor 10 höher als die Nutzfrequenz.
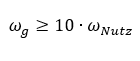
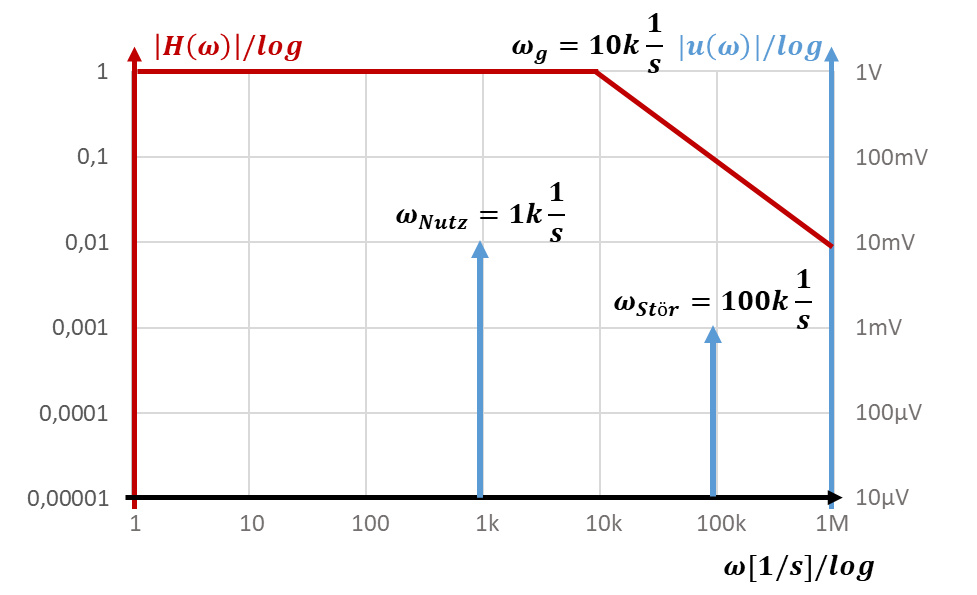
Legen wir die Grenzfrequenz zunächst auf den Wert ωg = 10k 1/s. Das Bode-Diagramm dazu sieht folgendermaßen aus:
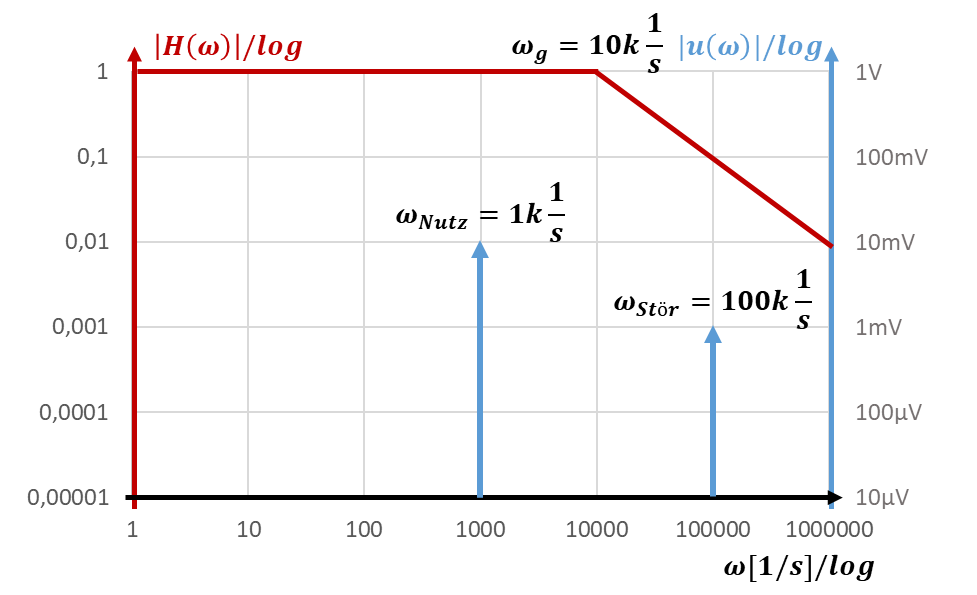
Das Filter mit dem roten Bode-Diagramm verstärkt das Nutzsignal mit |H(ωNutz)| = 1 und das Störsignal mit |H(ωStör)| = 0,1. Sie können diese Verstärkung am y-Wert der linken Achse bei den jeweiligen Signalfrequenzen ablesen.
Ein anderes Filter mit der Grenzfrequenz ωg = 100k 1/s sieht folgendermaßen aus:
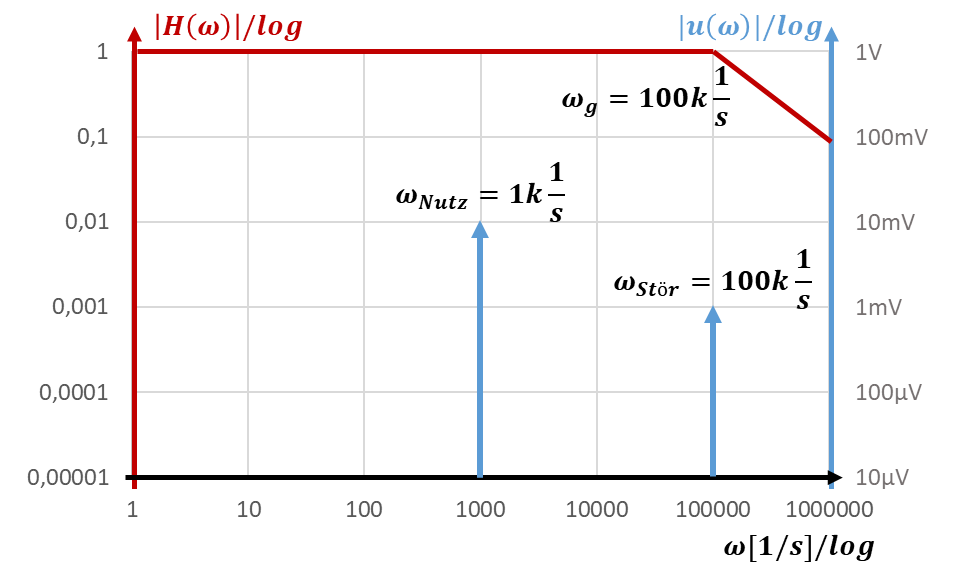
Dieses Filter verstärkt das Störsignal ebenfalls mit |H(ωStör)| = 1 (mit Bode-Näherung) oder genauer mit |H| ≈ 0,7 (ohne Bode-Näherung). Der Spitzenwert des Störsignals wird durch dieses Filter kaum reduziert. Das Filter mit der Grenzfrequenz bei ωg = 10k 1/s ist besser geeignet. Generell gilt:
Berechnung der Verstärkung
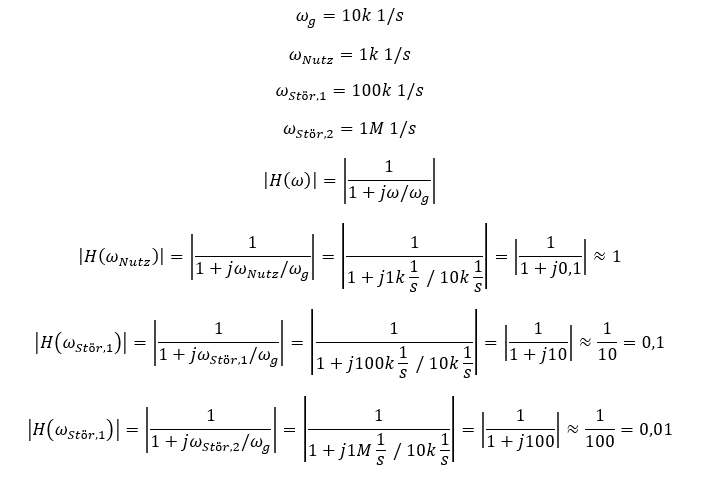
Sie nutzen das Bode-Diagramm als Vereinfachung, um nicht mehr rechnen zu müssen. Sie können die Verstärkung eines Filters dennoch ausrechnen. Dafür setzen Sie die Kreisfrequenz ω in die Übertragungsfunktion ein, bei der Sie die Verstärkung berechnen wollen. Wir nutzen ein neues Beispiel:
Dämpfung
Die Dämpfung ist der Kehrwert der Verstärkung. Der Begriff hat sich in der Messtechnik durchgesetzt, obwohl mit der Verstärkung bereits alle Effekte beschrieben werden können. Wird ein Signal z. B. mit Faktor 0,01 verstärkt, können wir auch sagen, dass es um Faktor 100 gedämpft wird. Es ist sprachlich griffiger zu sagen, dass ein Signal um Faktor 100 gedämpft wird, als dass es um 0,01 verstärkt wird. Es gilt als Formel
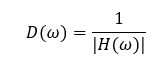
Die Dämpfung ist – genau wie die Verstärkung – abhängig von der Frequenz. Die Dämpfung ist nur eine neue Vokabel ohne echte neue Bedeutung.
Frequenz und Kreisfrequenz
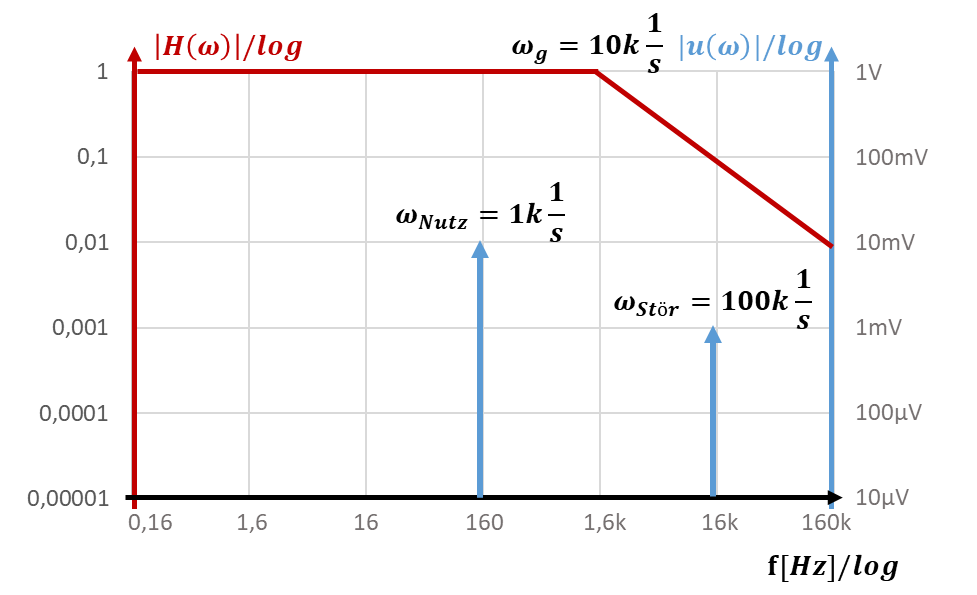
Bisher wurden alle Berechnungen mit der Kreisfrequenz ω durchgeführt. Die Kreisfrequenz ist eine wenig anschauliche Größe. Sie können alle Filter-Betrachtungen auch mit der Frequenz f durchführen. Es gilt:
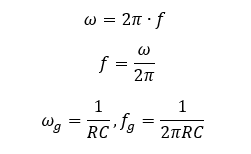
In der Praxis werden Sie beiden Darstellungen begegnen. Wählen Sie die Form mit ω, dann ist die Berechnung der Kreisfrequenz einfacher, denn der Faktor 2π entfällt. Frequenzen werden üblicherweise in f angegeben. An der Steckdose liegt z. B. f = 50 Hz an. Sie können diese Frequenz in eine Kreisfrequenz von ω = 314 1/s umrechnen. Im Bode-Diagramm verschiebt sich die x-Achse um den Faktor 2π, wenn Sie dieses in f angeben. Das zeigt folgendes Bode-Diagramm mit der Kreisfrequenz ω und danach mit der Frequenz f auf der x-Achse. Achten Sie auf die x-Achsen der beiden folgenden Abbildungen für den Unterschied.