Pendelschwingung
Ein Beispiel für ein schwingendes bzw. oszillierendes System ist eine Schaukel. Nachdem sie angestoßen worden ist, schwingt eine Schaukel hin und her. Ein Pendel, das an einem Faden hängt, schwingt ebenfalls hin und her. Ein anderes Beispiel ist ein Gewicht, das senkrecht an einer Spiralfeder hängt. Zieht man das Gewicht aus der Ruhelage kurzzeitig nach unten, schwingt es anschließend auf und ab. Wir betrachten in diesem Tutorial das Pendel als relativ einfaches Beispiel. Sehen Sie sich dazu bitte folgendes Video an:
Bringen wir das Pendel in ein Koordinatensystem, um seine Bewegung mathematisch beschreiben zu können:
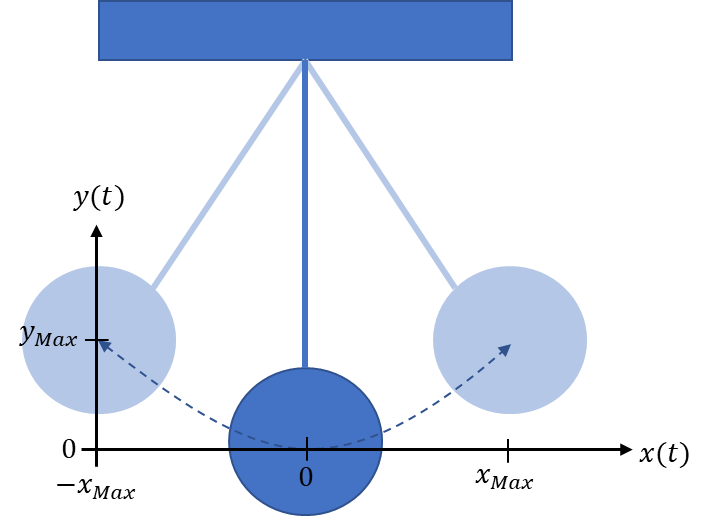
In dunkelblau sehen Sie das Pendel in Ruhelage. Lenken wir das Pendel z. B. nach links in die hellblau dargestellte Position aus, schwinge es anschließend zur rechts dargestellten hellblauen Position und wieder zurück. Die Geschwindigkeit der Bewegung ist an den hellblauen Endpunkten v = 0. Sie ist an der dunkelblauen Startposition maximal groß. Je näher das Pendel einer Endlage kommt, desto langsamer wird die Bewegung.
Ein System ist schwingfähig, wenn Energie zwischen zwei gekoppelten Speichern ausgetauscht werden kann. Wenn ein schwingfähiges System angeregt bzw. angestoßen wird, dann schwingt es i. A. Die Schwingung zu verhindern ist schwieriger als es zum Schwingen zu bringen, denn das Schwingen ist sein „natürliches“ Verhalten.
Alles, was sich außerhalb von Vakuum bewegt, reibt sich an Luft oder an einer Oberfläche. Reale Schwingungen klingen mit der Zeit ab, weil z. B. Reibung eine Bewegung verlangsamt. Wir betrachten zunächst ideale schwingende Systeme, die nach einer Anregung unendlich lange weiterschwingen.
Mathematik einer Pendelschwingung
Wir betrachten die Schwingung möglichst ohne Formeln. Wir zeichnen die Beobachtung des Verlaufs von X-Position und Y-Position aus dem Video über der Zeit. Die Bewegung eines schwingenden Pendels verläuft sinusförmig.
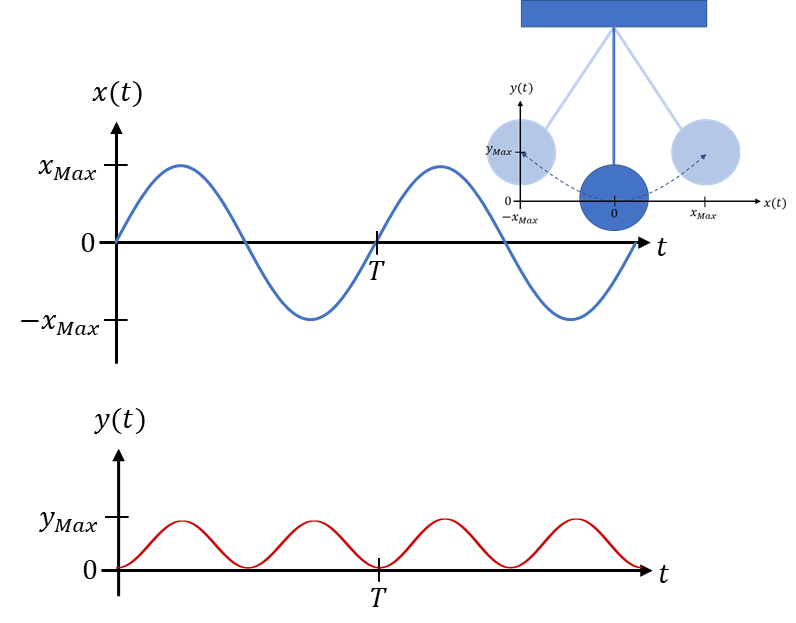
Das Pendel startet seine Bewegung zum Zeitpunkt t = 0 in der dunkelblauen Startposition. Zu Beginn gelten x = 0 und y = 0. Es startet seine Bewegung durch einen Impuls von außen in Richtung x, also nach rechts. Dadurch steigt die y-Position bzw. seine Höhe. Es erreicht bei einer Viertelperiode bei t = T/4 seine rechte Endlage mit maximal großer Höhe. Es bewegt sich anschließend bis zur linken Endlage bei t = 3T/4. Auch hier ist die y-Position maximal positiv, die x-Position aber nach dem gewählten Koordinatensystem maximal negativ. Nach einer Periode der Schwingung bei t = T erreicht das Pendel wieder die dunkelblaue Startposition. Es gelten folgende Formeln:
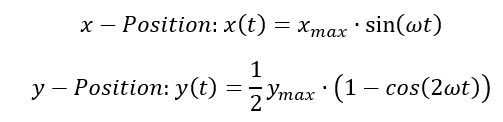
Wenn Sie mit der Mathematik Schwierigkeiten haben, genügt es die Zeitverläufe zu betrachten. Die zentralen Zusammenhänge werden auch ohne Formeln ersichtlich. Die Formeln bringen sie nur in eine mathematische Beschreibung, die einigen bei der Veranschaulichung hilft. Die Formeln sind also nicht immer und nicht für jeden hilfreich.
Die x-Position wird über einen Sinus beschrieben, in dem die Zeit t als Variable enthalten ist. Die Position x(t) ändert sich ja mit der Zeit t. Die y-Position ist um den Spitzenwert nach oben verschoben, so dass der verschobene Sinus nur positive Werte aufweist. Die Frequenz ist doppelt so hoch wie bei der x-Position. Der Sinus ist um π/2 nach rechts verschoben, so dass wir den Sinus auch als „-cos“ schreiben können. Die Formeln müssen Sie nicht aufstellen können, Sie sollten ihre Gültigkeit aber aus den Verläufen über der Zeit nachvollziehen.
In einem schwingenden System wird Energie zwischen zwei Energiespeichern hin- und hergeschoben. Beim Pendel sind die beiden Energieformen die potentielle Höhenenergie und die kinetische Bewegungsenergie. Schauen Sie dazu bitte folgendes Video:
Es gilt:
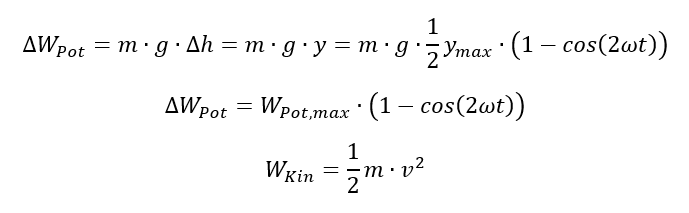
Die potentielle Energie können wir über die y-Position und die Masse des Pendels berechnen. Hinweis: Wir betrachten nur die Änderung der potentiellen Energie ΔWPot. Die Potentielle Energie in der dunkelblauen Startposition definieren wir für das lokale Experiment als 0, obwohl sie weit oberhalb des Erdkerns liegt und somit natürlich nicht 0 beträgt.
Die Geschwindigkeit des Pendels ist ebenfalls sinusförmig. Sie entspricht der zeitlichen Ableitung der Position. Für die Geschwindigkeit vereinfachen wir das Problem etwas. Wir nutzen aus, dass das Pendel sich vorwiegend in x-Richtung bewegt. Dann können wir die y-Geschwindigkeit in der Berechnung vernachlässigen. Insgesamt verläuft die Gesamt-Geschwindigkeit in der gleichen Kurvenform wie die Geschwindigkeit in x-Richtung, wir machen also keinen schlimmen Fehler. Es gilt:
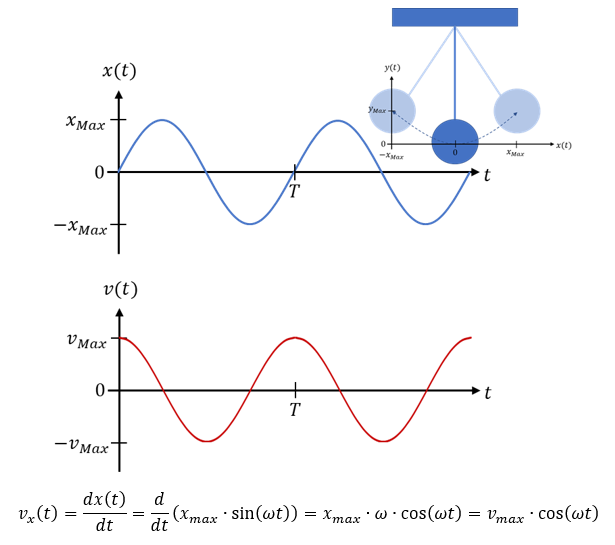
Wir brauchen für die kinetische Energie das Quadrat der Geschwindigkeit v2.
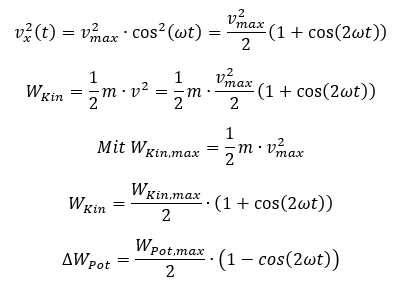
Die Energieformen weisen sehr ähnliche Formen auf. Die Spitzenwerte sind gleich groß, denn die Energie wird jeweils von der kinetischen Energie vollständig in potentielle Energie umgewandelt (und umgekehrt). Wir können jetzt die prinzipiellen Verläufe der beiden beteiligten Energieformen zeichnen:
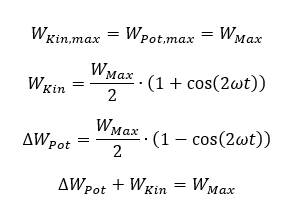
Die Summe der beiden Energien im System ist zu jedem Zeitpunkt gleich groß. Die Energie nimmt nicht ab oder zu, sie wechselt nur zwischen den beiden Energieformen hin und her.
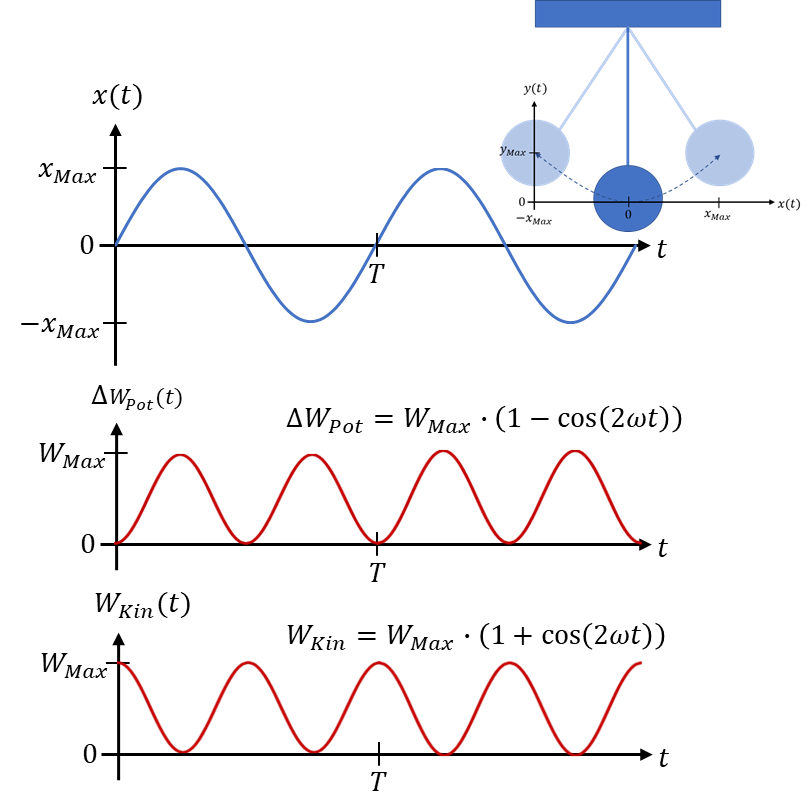
Am Punkt kleinster potentieller Energie (dunkelblaue Pendelstartposition) ist die kinetische Energie maximal groß. Hier schwingt das Pendel schnell vorbei. In einer Endlage der Schwingung (hellblaue Pendelposition) sind keine Geschwindigkeit und damit keine kinetische Energie vorhanden. Dafür ist die potentielle Energie maximal groß. Zwischen den Extremwerten ändern sich die Energien sinusförmig mit 180° Phasenverschiebung zueinander.
Alle anderen Beispiele für Schwingungen mit zwei Energieformen verlaufen nach ähnlichen Formeln. Die Energie wird zwischen den beiden beteiligten Energieformen sinusförmig hin- und hergeschoben. Die Gesamtenergie im System bleibt dabei konstant.
Weiter