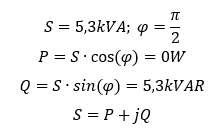Elektrische Leistung ist als Produkt aus Spannung und Strom definiert. Zunächst betrachten wir diese Größen im Zeitbereich.
Leistung im Zeitbereich
Im Zeitbereich gilt für sinusförmige Spannungen und Ströme:
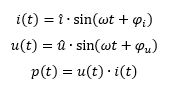
Betrachten wir zunächst nur den (einphasigen) Wechselstrom aus Grundlagen der Elektrotechnik, keinen Drehstrom. Wirkleistung P wird erzeugt, wenn Spannung und Strom in Phase sind, also bei φu = φi. Im einfachsten Fall sind beide Phasenwinkel 0. Betrachten wir die resultierende Leistung grafisch:
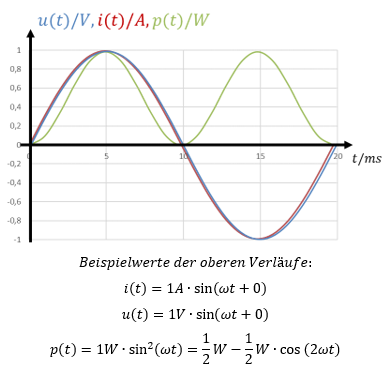
Spannung (blau) und Strom (rot) sind in diesem speziellen Fall in Phase, sie sind nicht zeitlich zueinander verschoben. Ich habe sie nur für die Grafik ganz leicht gegeneinander verschoben, damit beide Kurven sichtbar sind. Das Produkt aus u(t) und i(t) ist dann immer positiv. Die Leistung (grün) pulsiert allerdings über der Zeit, sie ist nicht konstant. Wenn solch eine Leistung aus einem Generator gezogen wird, dann wird die Achse des Generators mechanisch ungleichmäßig belastet. Das ist nicht gut. Wir wollen eine kontinuierliche elektrische Leistung über der Zeit haben.
Die Lösung liegt in einem 3-phasigen Drehstromsystem. Die Leistung in einem Drehstromsystem ist – aufgrund der Verschiebung von Spannung und Strom um jeweils 120° – auch um jeweils 120° verschoben. In der unteren Abbildung habe ich drei Mal die Leistung des oberen einphasigen Systems mit jeweils 120° Phasenverschiebung gezeichnet.
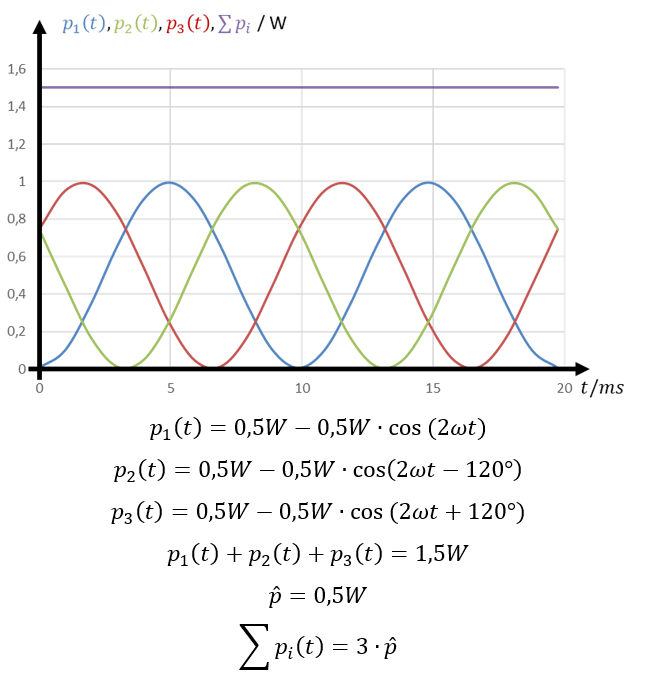
Jede der Leistungen liegt in diesem Beispiel im Bereich [0W … 1W]. Dieser Wert hängt natürlich von der Last ab und ist nicht immer gleich. Reine Wirkleistung liegt immer im Bereich 0W bis XW. Die Frequenz der Leistung ist doppelt so hoch wie die von Spannung und Strom. Die Summe der Leistungen ist – und das ist hier wichtig – zu jedem Zeitpunkt konstant. Sie können das an einfachen Zeitpunkten nachrechnen:
Bei t = 0 ms beträgt die Summe der drei Leistungen 0W + 0,75W + 0,75W = 1,5W.
Bei t = 5 ms beträgt die Summe der drei Leistungen 1W+0,25W+0,25W = 1,5W.
In symmetrischen Systemen gilt zu jedem Zeitpunkt:
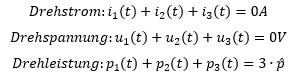
Die Summe der Leistungen ist nicht 0, weil die Sinus-Verläufe nicht um 0 herum liegen. Die Verläufe der Leistungen sind nach oben verschoben.
In einem Drehstromsystem haben wir erreicht, dass ein Generator kontinuierlich mit der gleichen konstanten mechanischen Leistung belastet wird. Der Achse des Generators ist es egal, welcher Elektromagnet gerade welche Einzelkraft ausübt, Hauptsache insgesamt ist die Kraft aller drei Elektromagnete über der Zeit konstant.
Komplexe Scheinleistung
Bisher haben wir nur Wirkleistung an Widerständen im Zeitbereich betrachtet. Ab jetzt arbeiten wir nur noch im Frequenzbereich mit komplexen Effektivwertzeigern. Bei Wirkleistung sind Spannung und Strom in Phase. Verbraucher mit komplexen Impedanzen benötigen i. A. Scheinleistung. Dafür benötigen wir Spannung und Strom an einer Last.
Die Drehspannung am Netz ist immer unveränderlich. Der Strom ergibt sich aus der Last.

Die Scheinleistung ist in jedem Strang gleich groß. Interessant ist, dass die Phase der Scheinleistung in jedem Strang gleich ist, obwohl die Phasen von Spannung und Strom sich in den Strängen unterscheiden. Die Scheinleistung gibt nur an, welchen Anteil Wirk- und Blindleistung eines Verbrauchers haben. Wirk- und Blindleistung geben an, wie Spannung und Strom zueinander phasenverschoben sind.
– Keine Phasenverschiebung: Nur Wirkleistung
– 90° Phasenverschiebung: Nur Blindleistung:
– Sonst: Mix aus beidem.
Die Phasenverschiebung kommt aus den Verbrauchern oder Lasten, denn die Spannungen sind starr. Ein Verbraucher verschiebt die veränderliche Phase des Stroms relativ zur Phase „seiner“ Spannung. Das tut bei symmetrischer Belastung jeder Verbraucher an jedem Strang auf die gleiche Weise. Am besten kann man das grafisch im Zeigerdiagramm erkennen.
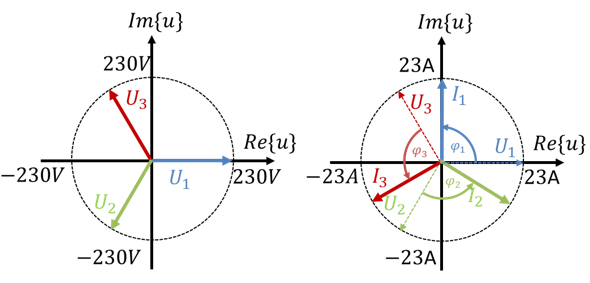
Links sehen Sie das Drehspannungssystem in Sternschaltung. Rechts sehen Sie den Strom aus dem Beispiel. Die Spannung ist gestrichelt im rechten Zeigerdiagramm eingezeichnet, damit wir deren Richtungen im Diagramm haben. Die Spannungszeiger haben in einem Strom-Zeigerdiagramm sonst nichts verloren. Die Phase zwischen Spannung und Strom ist in allen drei Strängen um 90° gedreht. Die Phasenwinkel der drei Stränge sind also gleich groß.
Der Winkel φU der Spannung zeigt an, wie die Spannung zeitlich zu einem festen Punkt t = 0s verschoben ist. Der Winkel φI des Stroms gibt an, wie der Strom zeitlich zu einem festen Punkt t = 0s verschoben ist. Der Winkel φ der Scheinleistung gibt an, wie Spannung und Strom relativ zueinander verschoben sind. Dabei spielen die absoluten Phasenlagen von U und I keine Rolle. Es interessiert nur deren relative Verschiebung. Und die sehen Sie im rechten Teil der oberen Abbildung. Sie sind alle drei gleich groß.
Dieser Zusammenhang ist ganz wichtig, deshalb erkläre ich es Ihnen nochmal im Zeitbereich in drei Abbildungen, die jeweils Spannung und Strom der drei Phasen darstellen:
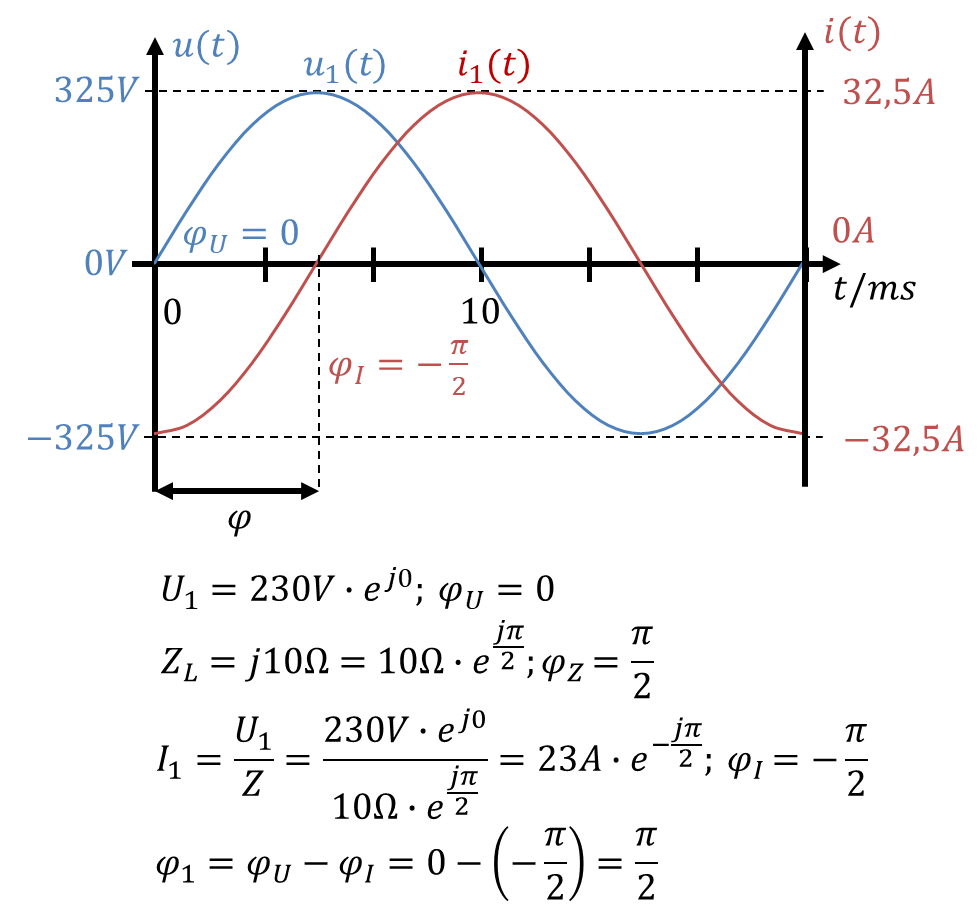
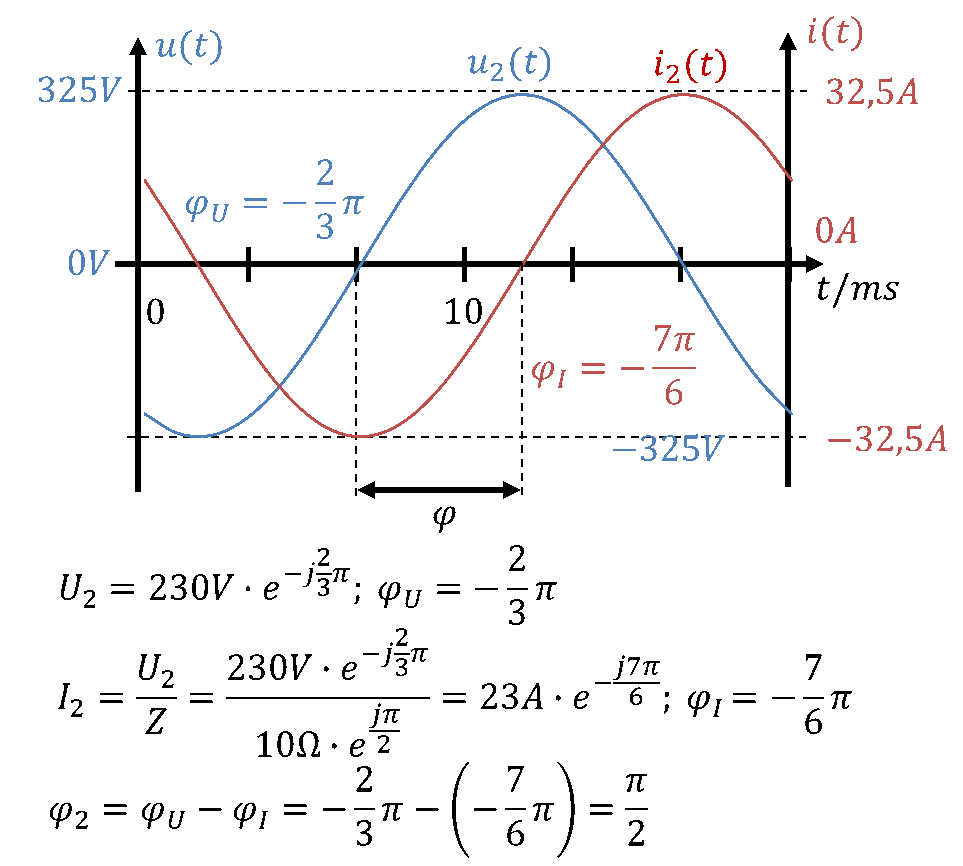
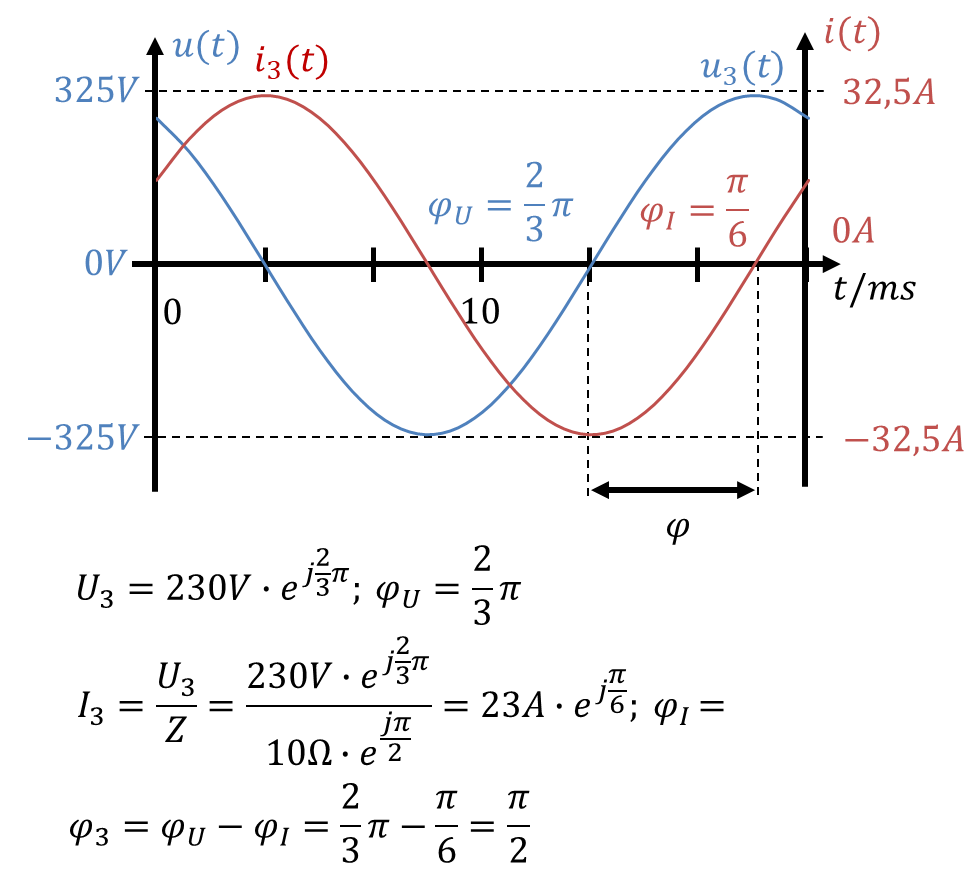
In allen drei Fällen ist der Phasenwinkel gleich groß. Die Effektivwerte von Spannung und Strom sind jeweils auch gleich groß, weil die Lastimpedanz gleich groß ist. Also sind auch die Scheinleistungen gleich groß.
Berechnen wir daraus die Wirk- und Blindleistungen. Es gilt