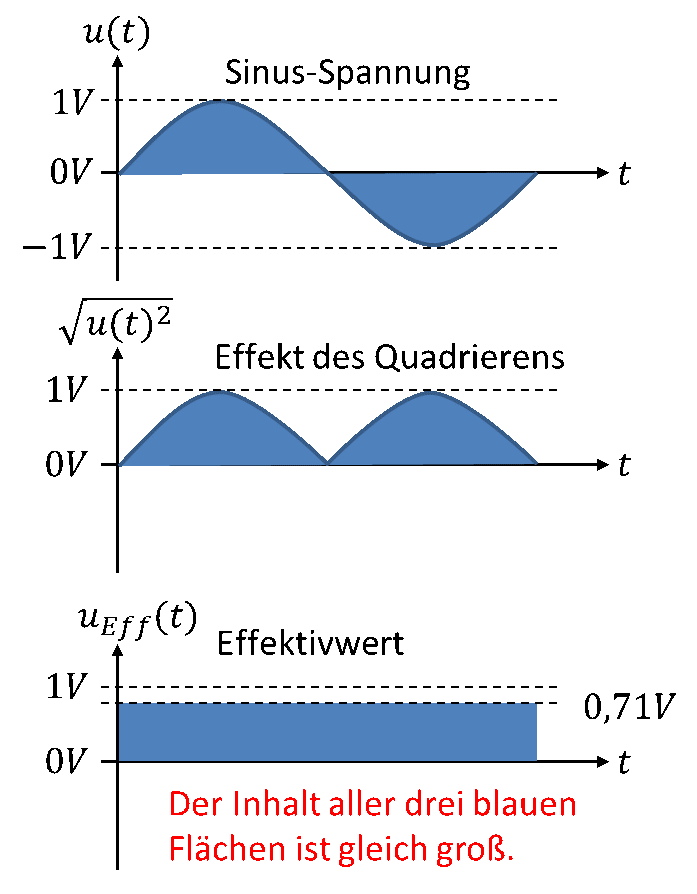Wenn Sie einen Fön an einer Steckdose betreiben stellt sich die Frage, wie viel elektrische Energie dabei in thermische Energie für die Hitze und kinetische Energie für die Luftbewegung umgesetzt wird. Bei Gleichstrom können wir die Leistung einfach als Produkt von Strom mal Spannung angeben. Bei Wechselstrom an einer Steckdose ist das nicht so einfach. Es stellt sich die Frage: Welche Leistung liegt im zeitlichen Mittel an? Welchen Parameter geben wir dafür an? Der Spitzenwert ist nicht geeignet, denn er liegt nur 2 Mal pro Periode kurzzeitig an. Weiter Parameter haben wir noch nicht.
In der Mathematik nutzen wir den Mittelwert für solche Angaben. Der Mittelwert einer Größe über der Zeit gibt an, wie viel der Größe im zeitlichen Mittel über eine bestimmte Zeit vorhanden war. Der Mittelwert beschreibt die Fläche unter dem Sinus über der Zeit. Der Mittelwert einer Größe bekommt einen waagerechten Strich über die Größe gezeichnet.
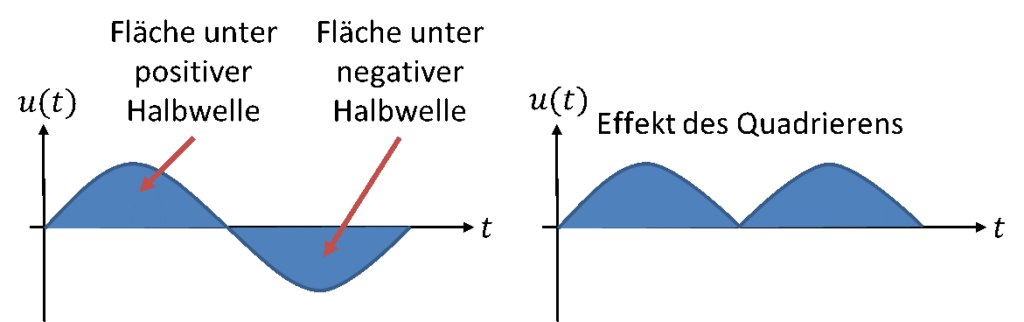
Bei sinusförmigen Größen haben wir das Problem, dass der Mittelwert über eine Sinusperiode immer 0 ergibt.
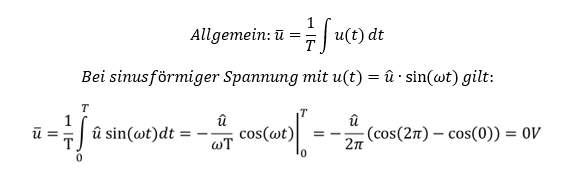
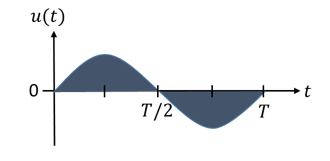
Die Fläche unterhalb der Zeitachse und die oberhalb heben sich bei der Summenbildung des Integrals gegenseitig auf. Sie sind gleich groß, weisen aber ein unterschiedliches Vorzeichen auf. Das zeigt der folgende Zeitverlauf der Spannung:
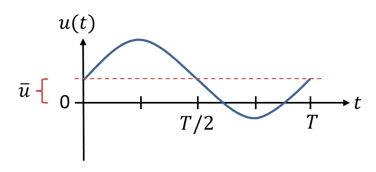
Der Mittelwert ist für symmetrische Wechselgrößen 0. Er hat für bestimmte Wechselgrößen eine andere Bedeutung: Ist eine Kurve auf der y-Achse verschoben, gibt der Mittelwert an, um welchen Wert die Kurve verschoben ist. Derartige Verläufe von Spannung und Strom betrachten wir aber noch nicht in den Grundlagen der Elektrotechnik. Die folgende Abbildung zeigt einen nach oben verschobenen Spannungsverlauf. Der Mittelwert gibt die Verschiebung mathematisch an.
In der Elektrotechnik wird der Mittelwert einer sinusförmigen Spannung nicht genutzt. Sie brauchen ihn also auch nicht berechnen zu können. Wir brauchen eine besser geeignete Größe zur Beschreibung der Fläche bzw. des „Gehalts“ einer sinusförmigen Spannung.
Wir brauchen für den „Gehalt“ der Sinusfunktion ein Maß, in dem beide Flächenanteile positiv berücksichtigt werden. Wenn die Funktion zunächst quadriert wird, dann aufsummiert und anschließend die Wurzel gezogen wird, dann erhalten wir ein Maß für die Fläche beider Anteile. Durch das Quadrieren wird der negative Flächenanteil positiv. Durch das Ziehen der Wurzel gleichen wir das Quadrieren mathematisch wieder aus. Dies realisiert der Effektivwert.
Der Effektivwert der Spannung u(t) ist als Formel folgendermaßen definiert:
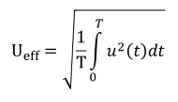
Setzen wir in die Formel einen sinusförmigen Spannungsverlauf ein, ergibt sich folgendes Ergebnis: Der Effektivwert einer sinusförmigen Größe entspricht dem Spitzenwert geteilt durch Wurzel(2). Es gilt:
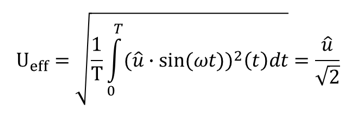
Der Effektivwert ist also ein Maß für den Betrag einer Fläche unterhalb einer Kurve. Wir berechnen den Effektivwert in diesem Tutorial (und auch in der Klausur) nicht mit Hilfe der Integralgleichung. Wir betrachten nur Effektivwerte von sinusförmigen Größen, die mit der Vereinfachung oben sehr einfach berechnet werden können.
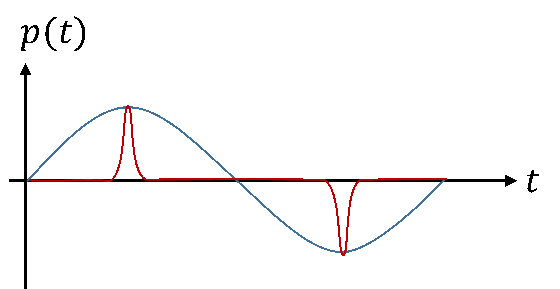
Kann man den „Gehalt“ einer Kurve nicht aus anderen Parametern einfacher gewinnen? Folgendes Beispiel zeigt, dass das nicht klappt. In der unteren Abbildung sind zwei Spannungsverläufe über der Zeit dargestellt. Die klassischen Parameter der Spannungen sind alle gleich: Spitzenwert, Periodendauer und Frequenz. Nur ist der rote Verlauf nicht sinusförmig. Offensichtlich sind die Flächen unterhalb der Verläufe nicht gleich groß. Wären dies Verläufe der Leistung über der Zeit am Fön an der Steckdose, würde der Fön beim blauen Verlauf ordentlich heiß werden, beim roten nur lauwarm. Für den roten Verlauf müssten wir den Effektivwert aus dem Integral bestimmen, denn die Funktion ist kein Sinus.
MerkeDer Effektivwert ist eine über der Zeit konstante Größe. Die Fläche, die der Effektivwert mit der x-Achse aufspannt, entspricht der Fläche, die der Sinus mit der x-Achse aufspannt.