Jetzt übertragen wir diese Mathematik mit x, y und z auf die Welt von P, UOS und R. Wir bilden die partielle Ableitung der Formel zur Berechnung der Zahl am ADC nach allen Parametern, die Unsicherheiten unterliegen. Die Parameter in diesem Beispiel sind:
Sensorspannung US
Offset-Spannung des OPs UOS
Widerstand R1
Widerstand R2
Referenzspannung des ADCs URef
Wir bilden also die Ausdrücke:
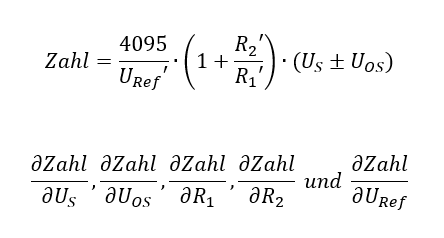
Anschließend bestimmen wir die Unsicherheit der Parameter. Die haben wir im vorherigen Kapitel bereits berechnet, es gilt:
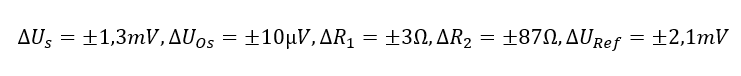
Mit diesen Ergebnissen können wir die Unsicherheit der Zahl am Ausgang des ADCs berechnen. Die Unsicherheit wird nach der Gauß´schen Fehlerfortpflanzung mit dieser Formel berechnet:
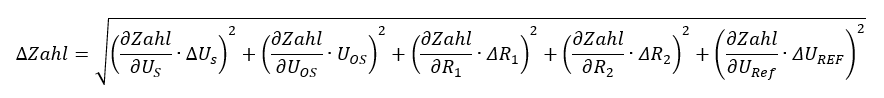
Sensorspannung
Beginnen wir mit der Sensorspannung US. Alle anderen Parameter werden zu Konstanten. Wir setzen die Unsicherheiten der anderen Parameter für diese Berechnung zu 0. Die Werte der anderen konstanten Parameter setzen wir so wie es für den gewählten Arbeitspunkt P = 3 bar passt, also z. B. für die Sensorspannung US = 30 mV. Es gilt
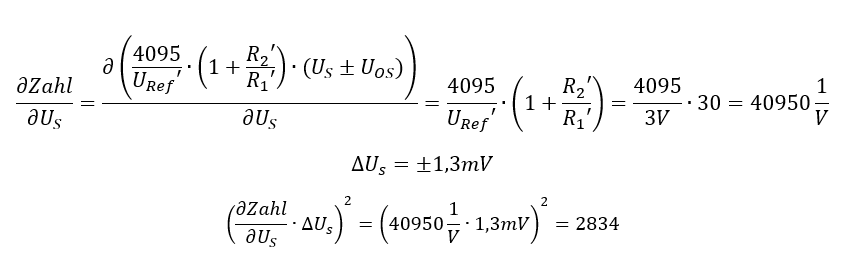
Der Einfluss der Unsicherheit der Sensorspannung auf die Zahl am Ausgang des ADCs ist also mit 2834 gewichtet. Betrachten wir als nächstes die Offset-Spannung des OPs:
Offset-Spannung des OPs
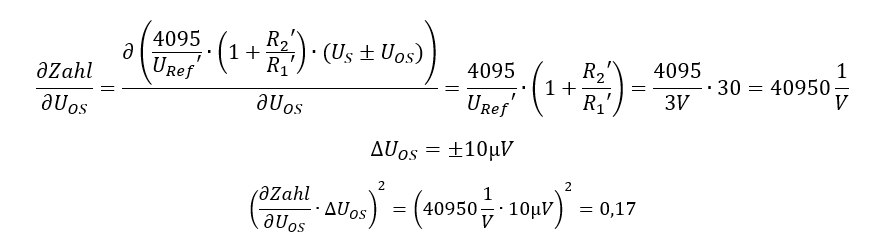
Die Offset-Spannung des OPs wird mit 0,17 gewichtet. Sie wirkt also viel weniger stark auf die Zahl am Ausgang des ADCs als die Unsicherheit der Sensorspannung. Das liegt daran, dass der Offset viel kleiner ist also die Unsicherheit der Sensorspannung. Als nächstes betrachten wir die Referenzspannung am ADC:
Referenz-Spannung des ADCs
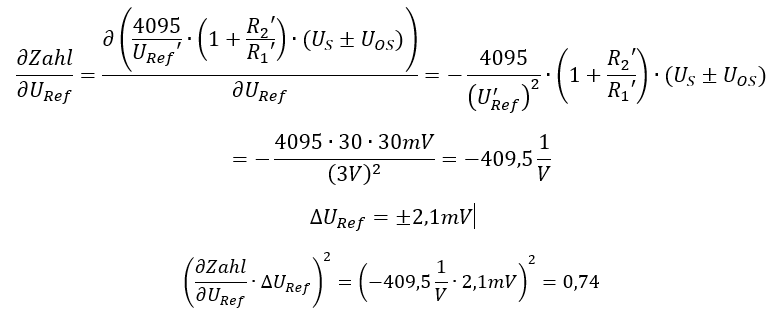
Die Referenzspannung des ADCs ist mit Faktor 0,74 gewichtet. Das ist unwesentlich mehr als die Offset-Spannung des OPs, und um viele Größenordnungen weniger stark als die Sensorspannung.
Widerstände
Aufgabe: Rechnen sie die Gewichtungsfaktoren für die Widerstände R1 und R2 selbst aus. Zur Kontrolle: Die Ergebnisse lauten 12,7 für R1 und für R2.
Ergebnis
Am Schluss bilden wir die Wurzel über all die Gewichtungsterme:

Zum Vergleich: Betrachten wir nur die Sensorspannung als Unsicherheit und setzen alle anderen Unsicherheiten zu 0, dann kommt als Ergebnis raus Δ Zahl = 53,23. Offensichtlich ist der Einfluss der Sensorspannung auf das Ergebnis dominant. Alle anderen Effekte spielen im Vergleich keine Rolle.
Interpretation
Es ist egal, welchen OP ich einsetze und wie genau die Widerstände sind, denn der Sensor ist im Vergleich so schlecht, dass er alleine die Unsicherheit des Systems dominiert. Wenn wir also an diesem System optimieren, dann verbessern wir den Sensor und setzen dafür schlechtere Komponenten an den anderen Stellen ein, um die Mehrkosten wieder einzusparen. Und dann rechnen wir erneut durch, wo als nächstes optimiert werden sollte.
Allgemein gilt: Unsicherheiten, die vor einem Verstärker auftreten, sind besonders ärgerlich. Die Unsicherheit wird mit dem Verstärkungsfaktor multipliziert und wirkt deshalb verstärkt auf den Ausgang. Deshalb ist es oft sinnvoll, zuerst alle Komponenten vor einem Verstärker zu optimieren, bevor die Komponenten hinter dem Verstärker angegangen werden. Die Unsicherheit am ADC spielt bei hoher Verstärkung oft überhaupt keine Rolle mehr.
Das Ergebnis der partiellen Ableitung wird bei diesem Verfahren quadriert. Anschließend wird die Wurzel gezogen, damit der Effekt des Quadrierens rückgängig gemacht wird. Damit wird mathematisch berücksichtigt, dass wir in den Unsicherheitsbereichen Normalverteilungen haben und keine gleichmäßigen Verteilungen. Der Effekt ist aber heftig: Große Gewichtungsfaktoren werden noch größer und kleine noch kleiner.
Wenn wir nur die einzelnen Unsicherheiten ohne das Gauß-Verfahren vergleichen, dann ist der Unterschied lange nicht so groß wie im mathematisch richtigen Ergebnis nach Gauß. Es muss die Wirkung der Unsicherheiten auf das Ergebnis betrachtet werden, nicht nur die Größe der Unsicherheiten. Manche Unsicherheiten werden z. B. verstärkt, andere nicht.