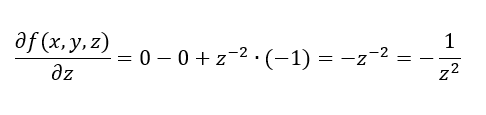Partielle Ableitung
Dazu ein Einschub zum partiellen Ableiten. Nehmen wir ein Beispiel aus der Schulmathematik mit
\[ f(x, y, z) = 13x - 5y^2 + \frac{1}{z} \]
Es gibt drei Parameter: x, y und z. Wenn wir die Formel nach x ableiten, dann sind y und z Konstanten. Alle Zahlen, die sich nicht ändern, wenn wir x variieren, sind bezogen auf x konstant. Wenn wir eine Konstante ableiten kommt als Ergebnis 0 raus. Die partielle Ableitung der Formel nach x lautet
\[ \frac{\partial f(x, y, z)}{\partial x} = 13 - 0 + 0 = 13 \]
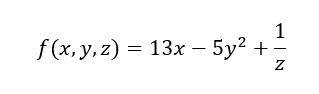
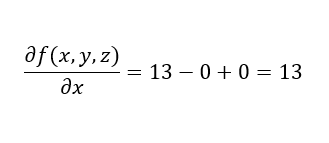
Es bleibt nur der Vorfaktor von x stehen. Wenn wir die gleiche Funktion nach y partiell ableiten, dann sind x und z Konstanten. Die Ableitungsregel für Polynome besagt, dass beim Ableiten der Exponent als Faktor mit dem Rest multipliziert wird. Dann wird der Exponent um 1 reduziert. Die Ableitung von 5y2 ist gleich 5y1 ∙ 2 = 10∙y.
\[ \frac{\partial f(x, y, z)}{\partial y} = 0 - 5y^{2-1} \cdot 2 + 0 = -10y \]
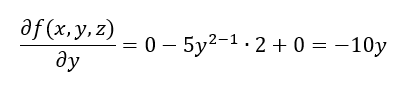
Die Ableitung nach z ist etwas komplizierter. Den Term 1/z schreiben wir dafür als z-1. Wir wenden die gleiche Regel an: Der Exponent -1 wird mit dem Rest multipliziert und dann um 1 reduziert. Die Ableitung von f(z) = 1/z ist damit:
\[ \frac{\partial f(x, y, z)}{\partial z} = 0 - 0 + z^{-2} \cdot (-1) = -z^{-2} = -\frac{1}{z^2} \]