Ein System schwingt, wenn sich sein Ausgang über der Zeit periodisch verändert. Ein Beispiel ist die Schaukel. Sie schwingt hin und her, sogar wenn man sie nicht weiter anschubst (Eingang = 0). Ein sinusförmiger Verlauf ist typisch für schwingendes Verhalten. Schwingen ist in der Regelungstechnik i. A. nicht gewollt. Wenn Sie einen Tempomaten im Auto betreiben, dann wollen Sie nicht, dass die Geschwindigkeit des Autos schwingt, sie soll konstant sein. Bei gewolltem Schwingen (wie an der Schaukel) stimulieren wir das System am Eingang so, dass es schwingt. Wenn ein System aus der Ruhelage heraus angestoßen wird, dann sehen wir, ob es schwingt. Das tun wir in der Regelungstechnik mit der Sprungantwort.
Mathematisch schwingt ein System, wenn seine Übertragungsfunktion das Verhalten
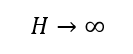
aufweist. Das gilt zum Beispiel, wenn der Nenner im Bruch der Übertragungsfunktion zu 0 wird. Das ist oft nur bei einer bestimmten Frequenz der Fall. Betrachten wir dazu ein System mit PT-1 Verhalten. Die Übertragungsfunktion lautet
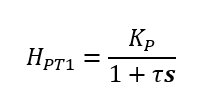
Damit der Nenner zu 0 wird und H unendlich groß wird, muss gelten τ ∙ s = -1. Der Parameter τ ist eine Zeit und somit in der Praxis immer eine positive Zahl. Die Frequenz s ist eine positive komplexe Zahl s = jω. Deshalb kann der Nenner nicht zu 0 werden. Ein System mit PT-1 Verhalten kann also nicht schwingen.
Ein Beispiel für ein schwingfähiges System ist ein Regelkreis mit einem I-System und einem I-Regler. Ich habe den Fall für Sie simuliert. In den folgenden Darstellungen sehen Sie das Modell und die Sprungantwort.
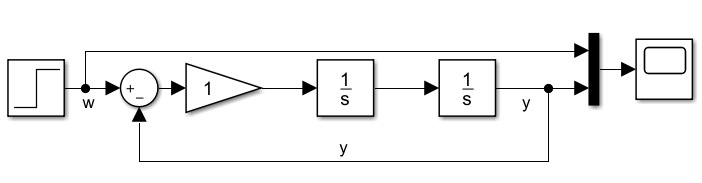
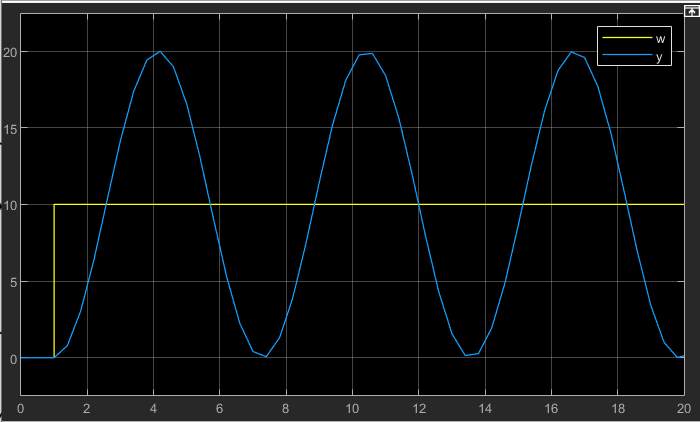
Das System schwingt dauerhaft, der Spitzenwert der Schwingung bleibt über der Zeit konstant. Wir sagen in der Regelungstechnik, das System schwingt ungedämpft. Wie können wir das mathematisch nachvollziehen?
Betrachten wir die Übertragungsfunktion des Regelkreises:
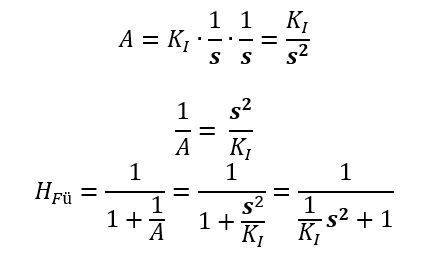
Wir setzen s = jω in die Gleichung ein. Mit j ∙ j = -1 folgt daraus
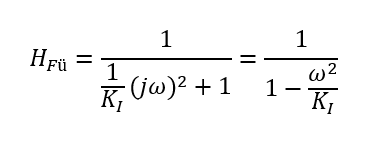
Der Nenner dieses Bruchs wird zu 0 für
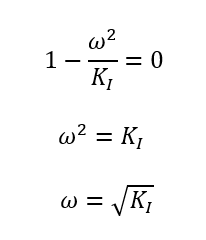
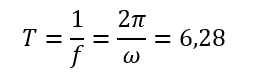
Verifikation: In der Sprungantwort können wir die Periodendauer z. B. über den Abstand der Maxima der Schwingung ablesen. Das erste Maximum liegt bei der Zeit 4(Sekunden), das zweite bei 10,3(Sekunden). Die Periodendauer der Schwingung beträgt also 6,3 (Sekunden). Die Berechnung stimmt mit der Simulation überein.
Eine Dauer-Schwingung wird über den Parameter „Schwingfrequenz“ charakterisiert. Dieser Parameter liegt entweder als Kreisfrequenz ω, als Frequenz f oder als Periodendauer T vor.
Aufgabe: Variieren Sie in der Simulation den Parameter KI und beobachten, wie sich die Frequenz ändert. Beachten Sie, dass gilt
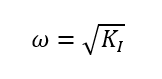
Nachdem wir schwingende Systeme betrachtet haben, legen wir jetzt den Fokus auf nicht schwingfähige Systeme.
Weiter