LaPlace-Transformation

Um Funktionsblöcke in den allgemeinen Regelkreis für den Parameter A einsetzen zu können, brauchen wir die Übertragungsfunktion der Blöcke. Die Übertragungsfunktion eines Funktionsblocks mit I-Verhalten können wir aber ohne Modifikation nicht beschreiben. Es gilt mit Eingang x(t) und Ausgang y(t) bei integrierendem Verhalten allgemein:

y(t) = y₀ + K_I ∙ $\int x(t)\; dt$
Wir können nicht einfach den Quotienten
$\mathrm{H(t)\; =}\frac{\mathrm{y(t)}}{\mathrm{x(t)}}$
bilden, den x(t) ist Argument eines Integrals. An dieser Stelle wenden wir den gleichen Trick an wie in der Wechselstromtechnik in Grundlagen der Elektrotechnik: Wir transformieren mit der LaPlace-Transformation. Damit vereinfachen sich mathematische Operationen wie Integration und Ableitung massiv.
Wenn wir die obere Gleichung aus dem Zeitbereich in den Frequenzbereich überführen, dann gilt:
y(t) = y₀ + K_I ∙ $\int x(t)\; dt$ mit y₀ = 0

$\mathrm{y(\omega )\; =\; K_I\; \bullet }\frac{\mathrm{x(\omega )}}{\mathrm{j\omega }}$
Jetzt können wir die komplexe Übertragungsfunktion bilden:
$\mathrm{H(\omega )\; =}\frac{\mathrm{y(\omega )}}{\mathrm{x(\omega )}}=\frac{\mathrm{K_I}}{\mathrm{j\omega }}$
Regelungstechniker verwenden einen etwas andere Frequenz-Parameter als Elektrotechniker. Die komplexe Frequenz ist ganz allgemein als
s = σ + jω
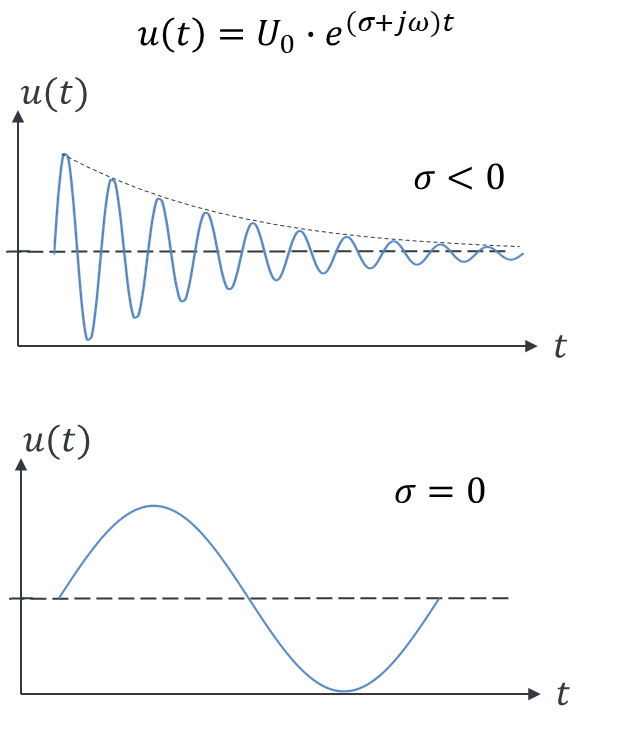
definiert. Dauerhafte ungedämpfte Schwingungen, deren Spitzenwert über der Zeit unveränderlich ist, werden mit s = jω mit σ = 0 berechnet. Das kennen Sie bereits. Der Parameter σ definiert die Dämpfung einer Schwingung. Wenn der Spitzenwert über der Zeit immer weiter abnimmt, dann ist ein σ im Spiel. Betrachten Sie z. B. die Schwingung einer Schaukel, die Sie loslassen. Die Schaukel schwingt mit der Frequenz jω hin und her. Sie wird aber auch langsamer und irgendwann steht sie still. Gründe dafür sind Reibung und Luftwiderstand. Bremsen führt zu einer Dämpfung der Schwingung. Für σ < 0 wird eine Schwingung gedämpf, bei σ = 0 ist sie ungedämpft und bei σ > 0 wird sie verstärkt, ihre Amplitude steigt also immer weiter an. Das betrachten wir hier aber nicht.

In dieser Vorlesung betrachten wir erst sehr spät gedämpfte Systeme, deshalb können Sie σ zunächst ignorieren. In der Regelungstechnik verwenden wir also die komplexe Frequenz s immer dann, wenn wir in der Elektrotechnik jω verwenden. Mathematisch ersetzen wir also in den Gleichungen jω immer durch s. Die komplexe Übertragungsfunktion eines Systems mit I-Verhalten beschreiben wir also als

$\mathrm{H(s)\; =}\frac{\mathrm{y(s)}}{\mathrm{x(s)}}=\frac{\mathrm{K_I}}{s}$
Diese Übertragungsfunktion können wir im allgemeinen Regelkreis einsetzen. Die Mathematik ist durch die Laplace-Transformation wieder einmal deutlich vereinfacht worden. I-Verhalten ist in der Regelungstechnik so wichtig und im Alltag in so vielen Systemen präsent, dass wir ab jetzt nur noch im Frequenzbereich arbeiten. Auch P-Verhalten kann im Frequenzbereich mit einer komplexen Übertragungsfunktion abgebildet werden. Diese ist zum Glück genau wie im Zeitbereich, denn es gilt für P-Verhalten
y(t) = K_P ∙ x(t)

y(s) = K_P ∙ x(s)
Wichtige Ergänzung: Der Buchstabe „s“ wird bereits für Sekunden verwendet. Wenn reale Systeme geregelt werden, kommen in den Formeln sowohl Sekunden als auch s als komplexe Frequenz vor. Um eine Verwechslung zu vermeiden, wird die komplexe Frequenz s immer als s fett dargestellt, die Sekunde s nicht.

Betrachten wir im nächsten Kapitel einen allgemeinen Regelkreis mit I-Verhalten.

Weiter