In einem System ohne Störungen (d = 0) gilt der Zusammenhang
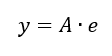
Betrachten wir zunächst ein A, das nur P-Verhalten mit KPR = 1 aufweist. Wenn es keine Regelabweichung gäbe, wäre e = 0 und damit immer y = 0. Wir wollen aber das y = w gilt. Wie kann dann anschaulich die Regelabweichung komplett verschwinden, sobald wir Speicher in A einsetzen? Die Antwort liegt in der Gleichung von Speichern im Zeitbereich. Setzen wir ein A mit reinem I-Verhalten mit KI = 1 ein, erhalten wir:
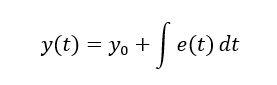
Der Wert von y(t) ist also vom aktuellen Wert von e(t) abhängig. Der Parameter y0 beinhaltet zusätzlich die komplette Vergangenheit der Regelabweichung über der Zeit. Es ist also nicht notwendig, dass die Regelabweichung e immer ungleich 0 ist, sondern es genügt, wenn sie in der Vergangenheit einmal ungleich 0 war. Mit e = 0 folgt in der Gleichung oben nämlich
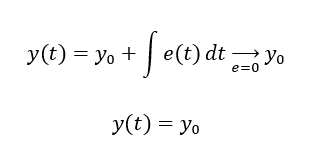
Ein Speicher hält seinen Ausgang y konstant, wenn der Eingang e = 0 ist. Der Füllstand eines Eimers bleibt konstant, wenn es keinen Zulauf gibt. Also weist ein Eimer am Ausgang y einen Füllstand ungleich 0 auf, wenn der Eingang e = 0 ist. Soll der Eimer auf den Soll-Füllstand ySoll = „halb voll“ gefüllt werden, läuft so lange ein Zulauf e hinein, bis y = ySoll gilt. Danach fließt nichts mehr hinein (e = 0) und der Eimer hält seinen Zustand am Ausgang konstant. Wir betrachten im Modell einen Eimer als System mit KIS = 1/A (Fläche A) und einem P-Regler mit KPR = 1:

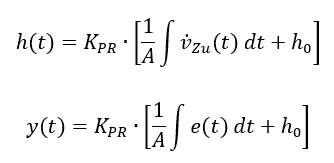
Betrachten wir jetzt einen Eimer mit Ablauf als Störung d. Wenn Wasser aus dem Eimer fließt, dann sinkt der Füllstand y. Um dies auszugleichen, wird ein Zulauf e benötigt, der genauso groß wie d ist. Dafür muss e = d ≠ 0 sein und wir haben wieder eine Regelabweichung e. Immer wenn wir eine Regelabweichung e benötigen, um eine Störung d zu kompensieren, erreichen wir das Ziel y = w nicht mehr. Der Speicher in A hilft immer dann nicht für e = 0, wenn die Störung zusammen mit der Regelabweichung integriert wird, wenn also die Störung im Blockschaltbild links vom Integral wirkt.
Betrachten wir die Formel des Füllstands in Abhängigkeit von Zu- und Ablauf:

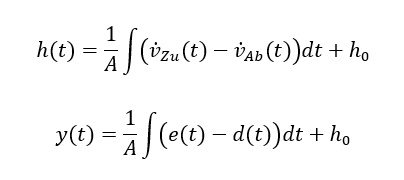
Die Formel führt nur zu einem konstanten Wert von y(t) = y0, wenn e(t) = d(t) gilt. Sobald keine Störung mehr wirkt (d = 0) ist das Problem nicht mehr vorhanden, denn dann gilt auch wieder e = 0.
Weiter