Um zu beurteilen, wie sich das geregelte System verhält, nutzen wir erneut die Sprungantwort. Damit können wir nicht nur Funktionsblöcke, sondern auch geregelte Systeme charakterisieren. Dazu wird im ersten Schritt die Störgröße d = 0 gesetzt und in der Führungsgröße w ein Sprung von 0 auf 1 initiiert. Dann wird die Ausgangsgröße y über der Zeit aufgetragen. Bei einem System mit A = 9 ergibt sich folgender Verlauf:
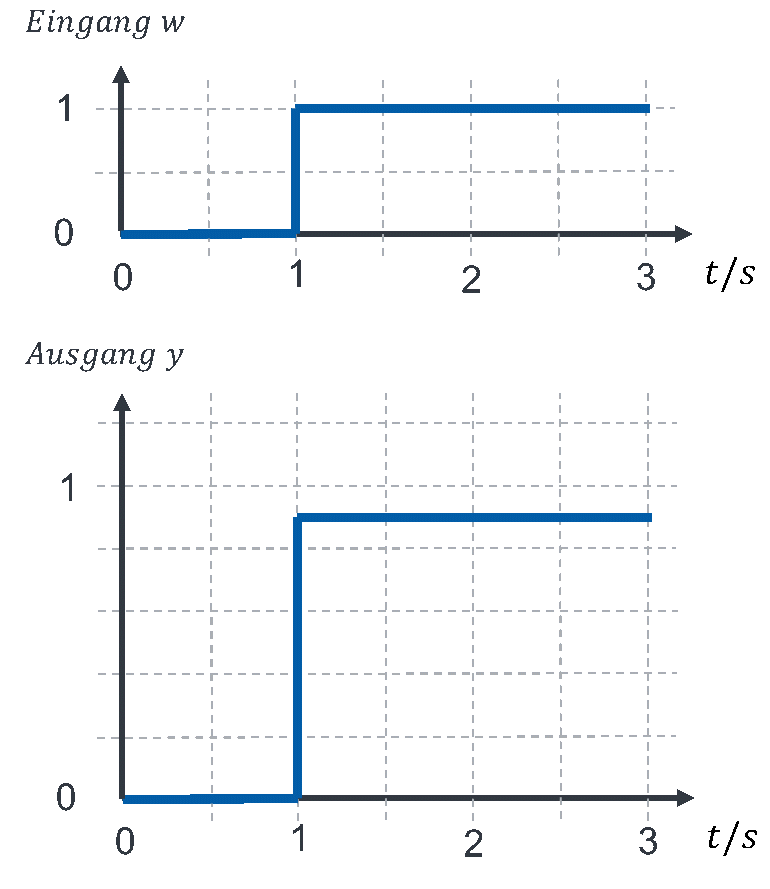
Die Regelgröße y springt zum gleichen Zeitpunkt wie ein Führungsgröße w. Da die Übertragungsfunktion des geregelten Systems den Wert
aufweist, springt der Ausgang y auf den Wert 0,9, wenn die Führungsgröße w von 0 auf den Wert 1 springt. P-Verhalten in A führt also zu P-Verhalten im geregelten System.
Das Führungs-Verhalten des geregelten Systems können wir folgendermaßen charakterisieren:
1. Es handelt sich um P-Verhalten
2. Der charakteristische Parameter lautet KP = HFü = 0,9.
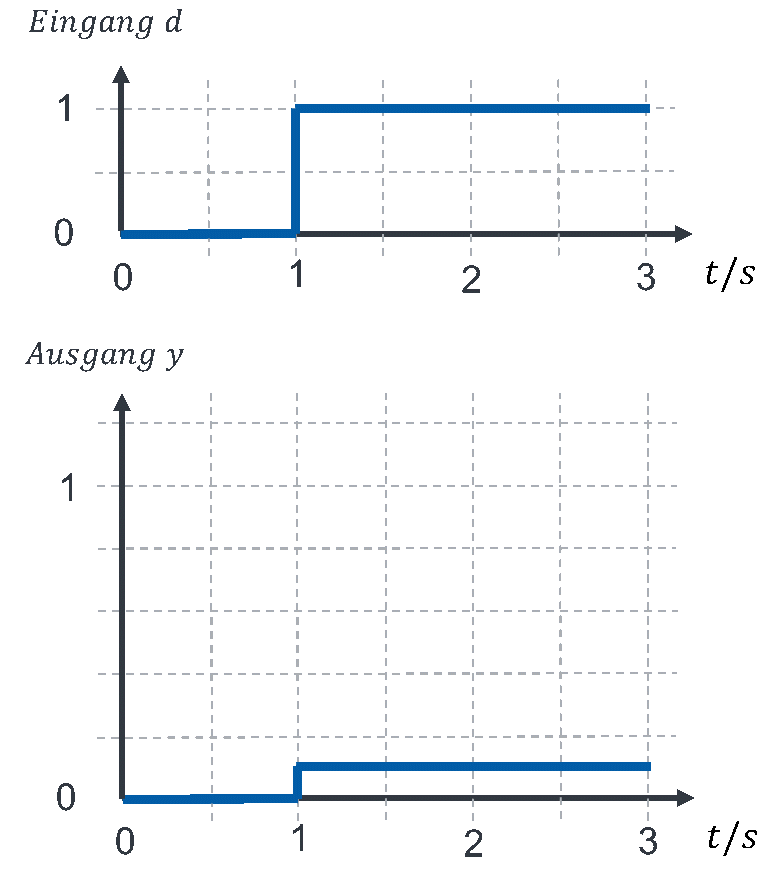
Als nächstes analysieren wir die Störunterdrückung. Dafür setzen wir w = 0 und d springt von 0 auf 1. Die Übertragungsfunktion lautet für A = 9:
Da die Übertragungsfunktion eine Konstante ist, handelt es sich erneut um P-Verhalten bei der Störunterdrückung. Sie lässt sich folgendermaßen charakterisieren:
1. Es handelt sich um P-Verhalten
2. Der charakteristische Parameter lautet KP = HSU = 0,1.
Die Sprungantwort sieht folgendermaßen aus: