Anschauliche Herleitung der komplexen Impedanz

Um den Zusammenhang zwischen Spannung und Strom an einem Kondensator bei Wechselstrom zu erklären, greifen wir auf die Analogie des Wassereimers mit Zu- und Ablauf aus Kapitel Rechnen mit Speichern zurück. Zulauf und Ablauf des Wassers erfolgen über die Wasserhähne sinusförmig, so dass sich auch der Füllstand sinusförmig ändert. Bitte schauen Sie sich die Grafiken am Anfang dieses Kapitels noch einmal an.

Frequenzabhängigkeit

Betrachten wir zunächst, wie Zulauf Z(t) und Füllstand f(t) von der Frequenz des Befüllens und Entleerens abhängen. Wird der Eimer mit f=1Hz befüllt und entleert, dann wird er innerhalb einer Sekunde einmal vollständig befüllt und wieder vollständig geleert. Sein Füllstand F8t) ändert sich sinusförmig, und nach einer Sekunde weist er wieder den ursprünglichen Füllstand auf.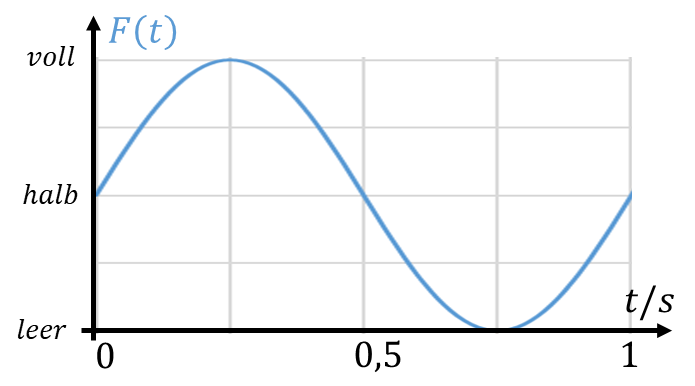

Wenn der Eimer zu Beginn der Befüllung nicht halb gefüllt ist, sondern er vollständig leer ist, dann wird er in einer Sekunde ebenfalls vollständig gefüllt, er ist am Ende aber wieder leer. Der Füllstand zu Beginn gibt uns also ein Maß für die Phasenverschiebung am Eimer.

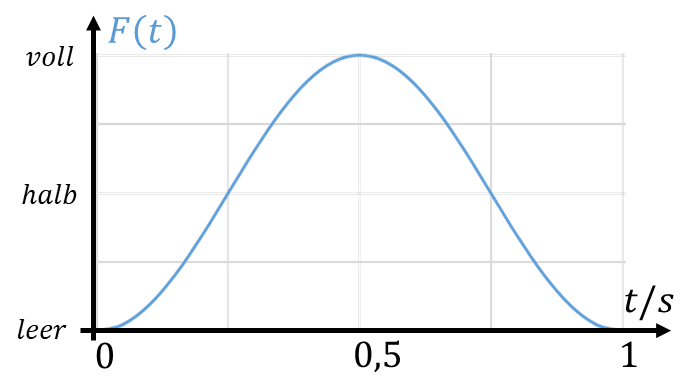
Wenn der gleiche Eimer mit der Frequenz f=2Hz betrieben wird, dann ist eine Periode T=0,5s lang, der Vorgang des Befüllens und Leerens ist dann doppelt so schnell. Im gleichen Zeit-Maßstab sieht der Verlauf folgendermaßen aus:

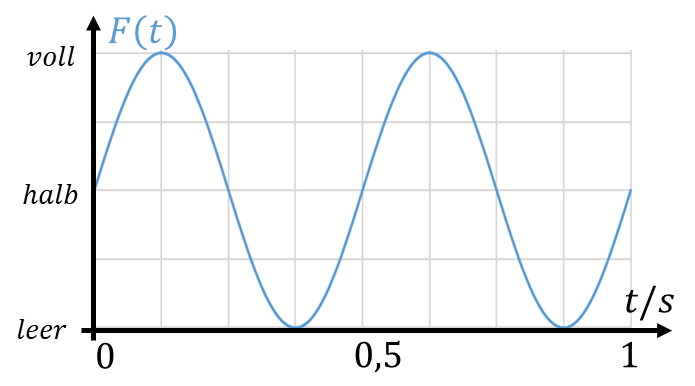
Um in einem Eimer mit der Grundfläche A_Eimer=100cm² den Füllstand von 0cm auf 10cm um Δh=10cm zu erhöhen, benötigen wir ein Wasservolumen von V_Eimer=A_Eimer*Δh=1000cm³. Wenn der Eimer mit f=1Hz betrieben wird, dann wird diese Wassermenge innerhalb einer halben Sekunde als Zulauf zugeführt und innerhalb einer halben Sekunde wieder abgeführt. Die Wassermenge pro Zeit, also die Zulaufgeschwindigkeit, ist eher langsam. Wird der gleiche Eimer mit einer Frequenz von f=2Hz betrieben, muss die gleiche Wassermenge in der halben Zeit bewegt werden. Die Zulaufgeschwindigkeit als Volumen pro Zeit muss dann 2 Mal so groß sein.

Zulaufgeschwindigkeit Z(t)~f
Analog dazu ist am Kondensator (Eimer) der Strom (Zulaufgeschwindigkeit) abhängig davon, wie schnell sich die Spannung (Füllstand) ändert, wie oft also das Wasservolumen (Ladung) pro Sekunde verschoben (umgeladen) wird. Der Strom am Kondensator I_C ist also proportional zur Frequenz f, mit der sich die Spannung U_C ändert, wenn Spannung und Strom beide sinusförmig sind.

I_C~f
Bei sinusförmigen Verläufen nutzen wir die Kreisfrequenz ω statt der Frequenz f. Mit ω=2πf können wir auch schreiben:

I_C~ω

Abhängigkeit von der Kapazität

Betrachten wir jetzt statt dem kleinen Eimer einen größeren Eimer mit doppelter Fläche A_Eimer2=200cm²=2*A_Eimer. Damit am Eimer 2 der Füllstand um Δh=10cm angehoben wird, ist ein Wasservolumen von V_Eimer2=A_Eimer2∙Δh=2000cm³=2∙V_Eimer notwendig. Damit muss pro Zeit doppelt so viel Wasser in den großen Eimer fließen als in den kleinen Eimer. Die Zulaufgeschwindigkeit ist also von der Grundfläche des Eimers abhängig. Am Kondensator ist der Strom (Zulaufgeschwindigkeit) proportional zur Kapazität C (Fläche) des Kondensators (Eimers).

I_C~C

Phasenverschiebung

Wir haben in Kapitel Rechnen mit Speichern festgestellt, dass der Füllstand immer dann maximal groß ist, wenn der Zulauf positiv war und seinen Nulldurchgang hat, also die Befüllung abgeschlossen ist und die Entleerung beginnt. Während der Zulauf positiv ist, steigt der Füllstand an. So lange der Zulauf negativ ist (also Wasser abläuft), sinkt der Füllstand. Wenn der Zulauf sinusförmig ist, gibt es eine Phasenverschiebung zwischen Zulauf und Füllstand von einer Viertel-Periode. Eine Zeitverzögerung von einer Viertel-Periode im Zeitverlauf des Sinus entspricht am Einheitskreis einer Phasenverschiebung von Δϕ=π/2.

Diese Phasenverschiebung zwischen Zulauf und Füllstand weist jeder Speicher auf, dessen Zulauf sich sinusförmig ändert. Es gilt auch für Spannung und Strom an den Bauteilen Spule und Kondensator. Die Spannung am Kondensator wird über das Integral des Stroms über der Zeit berechnet. Das Integral über der Zeit bildet die Summe des Stroms in der Vergangenheit ab. Es ist also auch mathematisch nachvollziehbar, dass ein positiver Strom erst zeitlich verzögert eine positive Spannung zur Folge hat.
In der Mathematik der komplexen Zahlen wird der Faktor „i“ für eine solche Phasenverschiebung genutzt. Da in der Elektrotechnik der Buchstabe „i“ für den Strom benutzt wird, nutzen wir stattdessen das kleine „j“, wenn die Mathematiker „i“ benutzen. Wird eine sinusförmige Spannung mit j multipliziert, wird dadurch die Phase um +π/2 verschoben. Das Signal wird in der Zeitdarstellung also um eine Viertelperiode nach links in Richtung Vergangenheit verschoben. Da der Zulauf gegenüber dem Füllstand um genau eine Viertelperiode nach links verschoben ist, können wir die Phasenbeziehung massiv vereinfachen.
Zunächst beschreiben wir den Verlauf des Füllstands F(t) mathematisch. Der halbe Füllstand „halb“ wird zum Zeitpunkt t=0s erreicht. Dazu wird eine Sinus-Funktion mit Spitzenwert „halb“ addiert. Also bekommen wir eine um „halb“ nach oben verschobene Sinus-Funktion:

Füllstand F(t)=halb+halb∙sin(ωt)
Für die mathematische Beschreibung des Zulaufs setzen wir „max.Leeren“=-„max.Füllen“. Damit bekommen wir die Gleichung

Zulauf Z(t)=max.Füllen∙sin(ωt+π/2)=j∙max.Füllen∙sin(ωt)~j∙F(t)

Zulauf~j∙Füllstand

Zusammenfassung

Bei sinusförmiger Befüllung stehen Zulauf und Füllstand eines Eimers in folgendem Zusammenhang: Der Zulauf ist proportional zur Kreisfrequenz ω, zur Fläche A und zu j∙Füllstand. Es ergibt sich die Formel (ohne Herleitung):

Zulauf(t)=jωA∙Füllstand(t)
Am Kondensator gilt:

i_C(t)=jωC∙u_C(t)
Bei der Spule gelten die Zusammenhänge wie beim Kondensator, nur muss u gegen i getauscht werden und L gegen C getauscht werden. Es gilt (ohne Herleitung) an der Spule:

u_L(t)=jωL∙i_L(t)

Komplexe Impedanz

In der Elektrotechnik werden Spannungen und Ströme in Schaltungen ausgerechnet. Dafür brauchen wir Maschen- und Knotengleichungen in den Schaltungen und an den Bauelementen die Bauelement-Gleichungen. Am Widerstand gilt als Bauelementgleichung das Ohm´sche Gesetz

U=R∙I
Wir suchen für Kondensator und Spule einen ähnlich einfachen Zusammenhang, denn mit den Integral-Gleichungen

$\mathrm{u_C=}\frac{1}{C}\mathrm{\bullet \int i_C(t)\; dt}$
und

$\mathrm{i_L=}\frac{1}{L}\mathrm{\bullet \int u_L(t)\; dt}$
will kein Mensch von Hand rechnen müssen. Wenn wir die in diesem Kapitel neu erarbeiteten Gleichungen so wie das Ohm´sche Gesetz umformen, dann gilt

U_L=jωL∙I_L
und

$\mathrm{U_C=}\frac{1}{\mathrm{j\omega C}}\mathrm{\bullet I_C}$
Wir definieren komplexe Impedanzen Z mit der Einheit Ohm (Ω) für das Verhalten von Strom und Spannung an Kondensatoren und Spulen für das komplexe Ohm´sche Gesetz Wir definieren komplexe Impedanzen Z mit der Einheit Ohm (Ω) für das Verhalten von Strom und Spannung an Kondensatoren und Spulen für das komplexe Ohm´sche Gesetz

U_R=Z_R∙I_R, U_C=Z_C∙I_C und U_L=Z_L∙I_L
mit

Z_L=jωL, $\mathrm{Z_C=}\frac{1}{\mathrm{j\omega C}}$ und Z_R=R.
Wichtig: Das gilt nur, wenn Spannung und Strom sinusförmig sind. Wir können jetzt in Wechselstrom-Schaltungen mit allen Ihnen bekannten Bauelementen Spannungen und Ströme genauso wie in Gleichstromschaltungen berechnen. Es gelten alle Ihnen aus der Gleichstromtechnik bekannten Gesetzte wie Maschengleichungen, Knotengleichungen, Spannungsteiler und Stromteiler. An den Bauelementen gilt jeweils das komplexe Ohm´sche Gesetzt.
Vorteil: Wir müssen an speichernden Bauelementen nicht mehr Ableiten oder Integrieren.
Nachteil: Wir haben jetzt einen Faktor j in den Gleichungen und müssen nach den Regeln der komplexen Zahlen rechnen. Dazu mehr in Ihrer Mathe-Vorlesung.

Weiter