Um eine Maschine drehen zu lassen brauchen wir drei sinusförmige Ströme, die um 120° phasenverschoben sind. Die Amplitude der Ströme hängt vom Rotorwinkel ab. Die Ströme drehen sich also mit dem Rotor mit. Die Ströme werden zu einem Gesamtstromzeiger addiert. Sie erzeugen das Gesamt-Statorfeld, dass sich ebenfalls mit dem Rotor dreht. Idealerweise liegt der Stromzeiger des Gesamtstroms um 90° in Drehrichtung zum Rotor versetzt, damit das Statorfeld den Stabmagneten des Rotors bestmöglich schiebt und zieht.
In diesem Kapitel geht es um eine geniale mathematische Vereinfachung zur Beschreibung des Gesamt-Stromzeigers.
Dreiecks-Mathematik
Zunächst wiederhole ich die Mathematik an rechtwinkligen Dreiecken, die wir später nutzen werden.
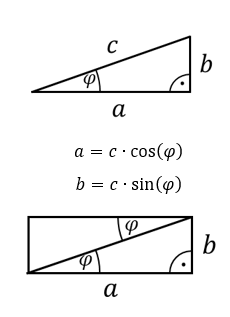
In der oberen Abbildung wird gezeigt, wie mit Hilfe von Sinus und Cosinus in einem rechtwinkligen Dreieck die Kantenlängen abhängig vom Winkel ausgerechnet werden können. Die Hypotenuse c ist die Seite, die nicht an den rechten Winkel angrenzt. Sie liegt dem rechten Winkel gegenüber. In den Beispielen weiter untern im Kapitel ist diese Länge immer gegeben.
Die Gegenkathete ist die Seite b. Sie liegt dem Winkel φ gegenüber. Sie ist eine Kathete, denn sie liegt direkt am rechten Winkel. Mit dem Sinus berechnen Sie die Länge der Gegenkathete.
Die Ankathete ist die Seite a. Sie liegt am Winkel φ. Mit dem Cosinus berechnen Sie die Länge der Ankathete.
In der unteren Abbildung wird daran erinnert, dass die beiden Winkel mit der Bezeichnung φ gleich groß sind. Das gilt immer dann, wenn Sie ein Rechteck mit einer Geraden in zwei Dreiecke halbieren. Die gegenüberliegenden Seiten des Rechtecks sind natürlich gleich lang. Dann müssen die gegenüberliegenden Winkel gleich groß sein. Das erkennen Sie, wenn Sie mit Sinus und Cosinus die Längen der Seiten der Dreiecke ausrechnen.
1. Transformationsschritt
Wir arbeiten ab jetzt mit Effektivwert-Zeigern statt mit Spitzenwert-Zeigern. Die Länge des Stromzeigers entspricht dem Effektivwert. Für Effektivwertzeiger gilt:
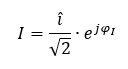
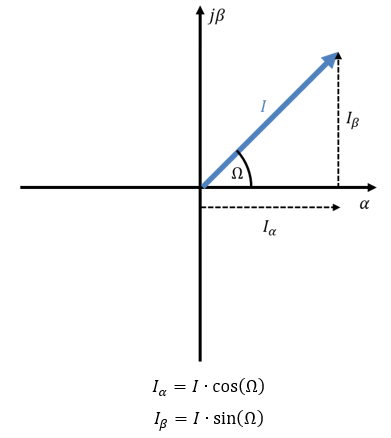
Im ersten Schritt werden die drei Ströme in ein neues Koordinatensystem überführt. Es wird ein Strom iα für den reellen Anteil des Stroms gebildet. Der imaginäre Anteil wird als iβ bezeichnet. Entsprechend werden die Bezeichnungen der Achsen angepasst.
Die allgemeine Formel oben gilt für jeden Rotorwinkel Ω. Wir wenden sie auf die Rotorwinkel-Positionen der drei Ströme an. Es gilt:
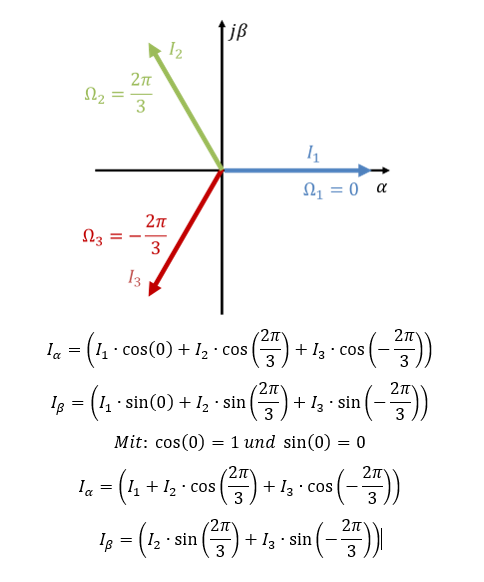
Der Strom I1 zeigt vollständig in Richtung α. Die anderen beiden Ströme enthalten Anteile der Richtungen α und β. Die Winkel für die Transformation sind fest, denn die Rotorwinkel der drei Ströme ändert sich nicht. Die drei Stromzeiger zeigen immer in die gleichen drei Richtungen.
Wir sind zwei orthogonale Achsen in Grafiken gewohnt. Drei Strom-Richtungen, die um ±120° statt um 90° zueinander gedreht sind, sind mathematisch und anschaulich unschön. Dieser erste Transformationsschritt bringt uns also die Einzelströme in ein gewohntes Koordinatensystem.
Das Koordinatensystem des Raumzeigers ist auf den Stator bezogen, es ist „statorfest“. Die Achsen des Koordinatensystems stehen still, der Rotor und der Gesamtstromzeiger drehen sich im Kreis.
2. Transformationsschritt
Anschließend setzen wir uns gedanklich auf den Rotor und drehen uns mit dem Rotor im Kreis. Wir setzen uns auf den Südpol des Stabmagneten und schauen nach außen auf den Stator. Die 6 Spulen ziehen dann an uns vorbei. Das Rotorfeld weist immer in die Richtung, in die wir blicken.
Wenn wir mit der Ansteuerung der Ströme alles richtig gemacht haben, dann befindet sich das Statorfeld in Drehrichtung um 90° hinter uns. Wenn wir eine Spule passieren, ist ihr Strom gerade bei 0A. Die Spule 90° in Drehrichtung vor uns hat den maximalen positiven Stromwert. Sie zieht uns an. Die Spule 90° in Drehrichtung hinter uns hat den maximalen negativen Stromwert. Sie stößt uns ab.
Es sind zwei Richtungen relevant: Die Richtung, in die wir schauen, bezeichnen wir als „d“ wie „direkt“. Die Richtung 90° voraus in Drehrichtung bezeichnen wir als „q“ wie „quer“. Wir benutzen diese beiden Richtungen als Achsen für ein neues Koordinatensystem.
Unsere Blickrichtung – die d-Achse – dreht sich. Damit dreht sich das Koordinatensystem im Kreis. Die Elektromagneten des Stators ziehen an uns vorbei. Innerhalb dieses drehenden Koordinatensystems zeigt der Rotor immer in Richtung d-Achse. Der Gesamt-Statorstrom bewegt sich in diesem Koordinatensystem nicht mehr, er ist zu einer statischen Größe geworden.
Es ist ein ziemlich abgefahrener Gedanke, ein rotierendes Koordinatensystem aufzusetzen, in dem rotierende Größen konstant sind. Es wird als rotorbezogenes Koordinatensystem bezeichnet. Die Wirkung dieser Transformation ist genial.
Betrachten wir in der folgenden Abbildung in schwarz das statorfeste αβ-Koordinatensystem und in rot das rotorbezogene dq-Koordinatensystem. Die dq-Achsen sind um den Rotorwinkel Ω (hier im Beispiel 30°) gedreht. In der unteren Abbildung sind zwei Ströme Iα und Iβ als orangefarbene Stromzeiger gegeben. Daraus sollen die Ströme Id und Iq berechnet werden. Ich gehe also davon aus, dass die erste Transformation bereits durchgeführt worden ist.
Wir können jetzt mit Hilfe der Dreiecks-Geometrie berechnen, wie groß d- und q-Ströme abhängig von α- und β-Strom sind. Der Strom Iqα entspricht z. B. dem Anteil des Stroms Iα, der in q-Richtung fließt.
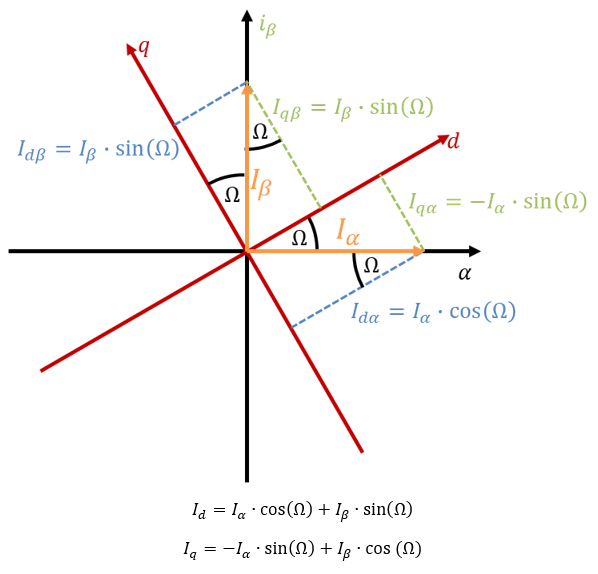
Diese Zusammenhänge gelten allgemein für alle Rotorwinkel Ω.
Zusammenführung beider Transformationsschritte
Um die d- und q-Stromzeiger im rotierenden Rotorkoordinatensystem zu berechnen, werden nacheinander beide Transformationsschritte durchgeführt. Es gilt:
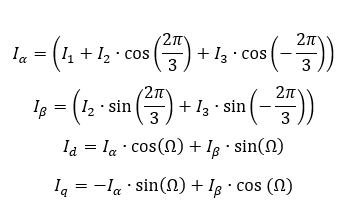
Die Ströme I1, I2 und I3 sind Effektivwertzeiger. Ihr Zeitverhalten ist bereits ausgeblendet. Sie weisen nur noch Länge und Richtung auf. Die Phasen (Richtungen) der Stromzeiger sind konstant. Wird der Spitzenwert aller drei Ströme verändert, dann ändern sich die Längen dieser Effektivwertzeiger. Damit das System symmetrisch belastet wird, sind die Spitzenwert der drei Ströme normalerweise gleich groß.
Die zweite veränderliche Variable in den Gleichungen oben ist der Rotorwinkel Ω. Alle anderen Parameter sind konstant. Wir können aus den Effektivwerten der Ströme und dem Rotorwinkel die Ströme Id und Iq berechnen.
Wenn der Statorstrom in Richtung q zeigt, dann zeigt der Stromraumzeiger immer um 90° in Drehrichtung vor den Rotor. Wir brauchen die Transformation also anders herum. Wir geben einen q-Strom als Sollwert vor, und müssen dann die Ströme I1, I2 und I3 berechnen. Die inverse zweite Transformation lautet:
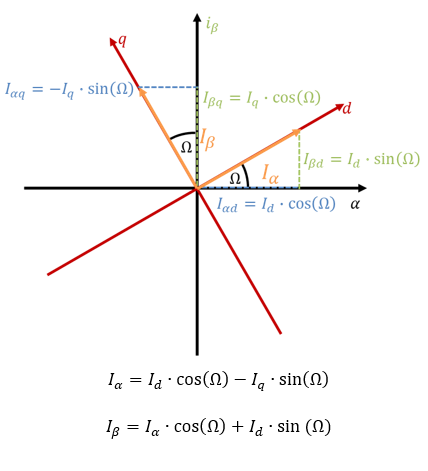
Die allgemeine Lösung der Inversion der ersten Transformation lautet:
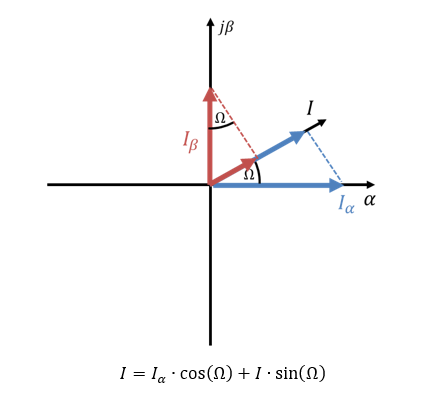
Wir wenden diese Formeln auf die festen Winkel der drei Statorströme an:
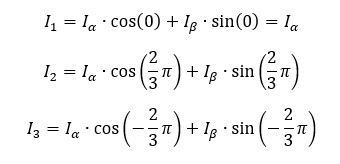
Angenommen ein Motor benötigt einen q-Strom in Höhe von Iq = 1A. Wie berechnen wir dazu die richtigen Ströme durch die Spulen?
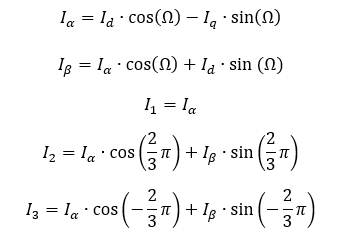
Der Anwender gibt vor, wie hoch d- und q-Ströme sind. Diese Angaben werden i. A. zur Steuerung der Maschinen eingestellt. Das Motorsteuergerät berechnet daraus für jeden Rotorwinkel die passenden Ströme an den Spulen.
Das d/q-Koordinatensystem zeigt immer mit der d-Achse in Richtung Südpol des Stators.
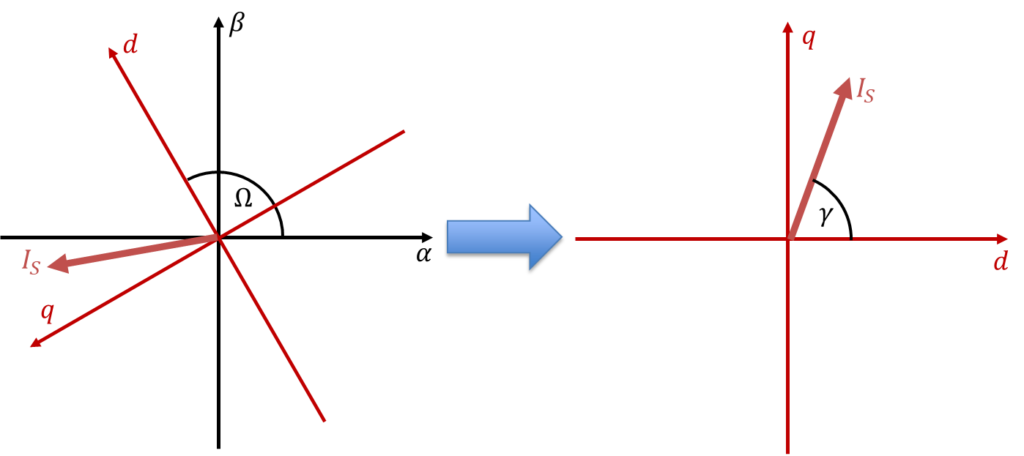
In dem Beispiel oben zeigt der Südpol des Stators auf 120°, also beträgt der Rotorwinkel Ω = 120°. Wenn sich der Rotor weiterdreht, dann zeigt die d-Achse ständig in eine andere Richtung. Wenn wir Ströme im d/q-Koordinatensystem betrachten, dann drehen wir das Koordinatensystem immer so, dass die d-Richtung nach rechts und die q-Richtung nach oben zeigt. Wir wissen, dass die d-Achse sich mit dem Rotor dreht. Wir tun bei der Transformation aber so, als ob unsere Blickrichtung immer nach rechts zeigen würde, wenn wir auf dem Rotor sitzen.
Ab jetzt verwenden wir die rechte Darstellung. In dieser Darstellung ist es völlig egal, wohin der Permanentmagnet zeigt. Wichtig ist nur, wie der Statorstromzeiger relativ zum Permanentmagneten ausgerichtet ist. Der Statorstromzeiger IS in der linken Abbildung dreht sich. In der rechten Abbildung steht er still. Damit kommen alle drehenden Größen zur Ruhe, sie werden statische Größen. Der Winkel Ω verschwindet konsequenterweise aus den Abbildungen.
Wir führen einen neuen Winkel γ ein, der die Verschiebung des Statorstromzeigers relativ zur d-Achse angibt. Dieser Winkel γ ist über einer Rotorumdrehung konstant. Er gibt nur an, wie der Statorstrom relativ zum Permanentmagneten verschoben ist. Bisher haben wir angenommen, dass γ immer -90° beträgt. Damit zeigt der Statorstromzeiger während der Rotordrehung immer 90° hinter den Südpol des Permanentmagneten.
Winkel Ω ändert sich während einer Rotorumdrehung, Winkel γ ist konstant. Der Rotor zeigt in Richtung Ω, das Statorfeld zeigt in Richtung Ω + γ.
Es folgt eine Animation zur Veranschaulichung des Transformationsschritte, die von Eirik Haustveit und Yngve Solbakken für ihrem Blog
switchcraft erstellt worden ist:
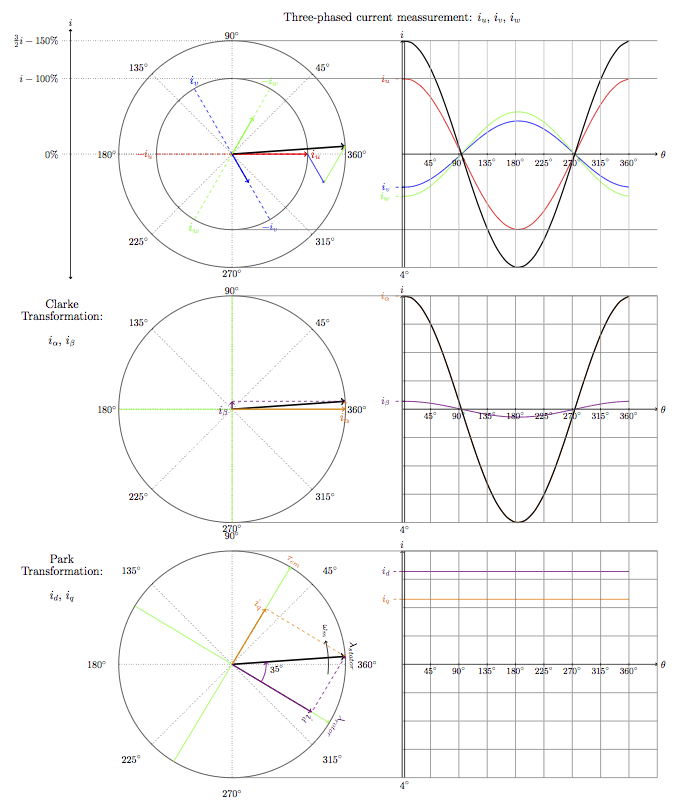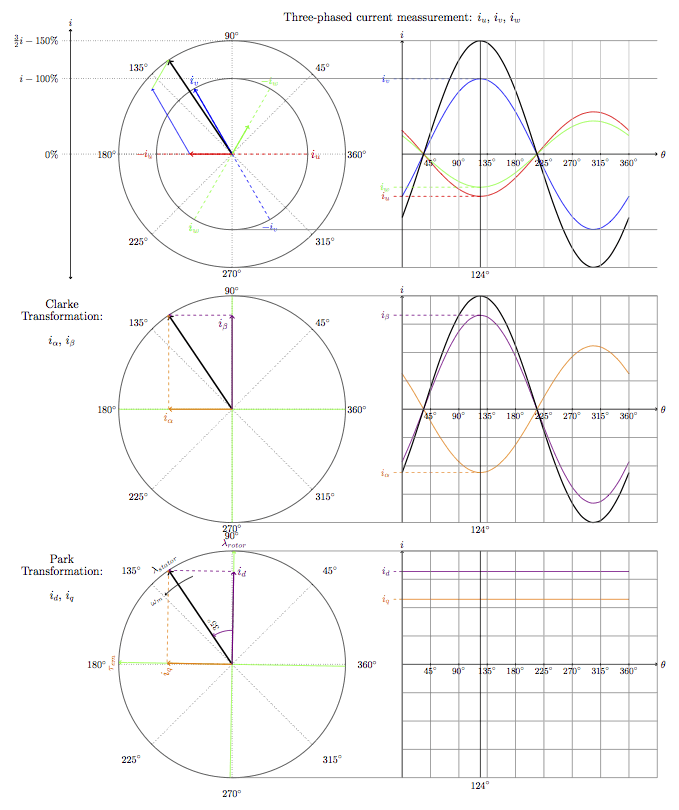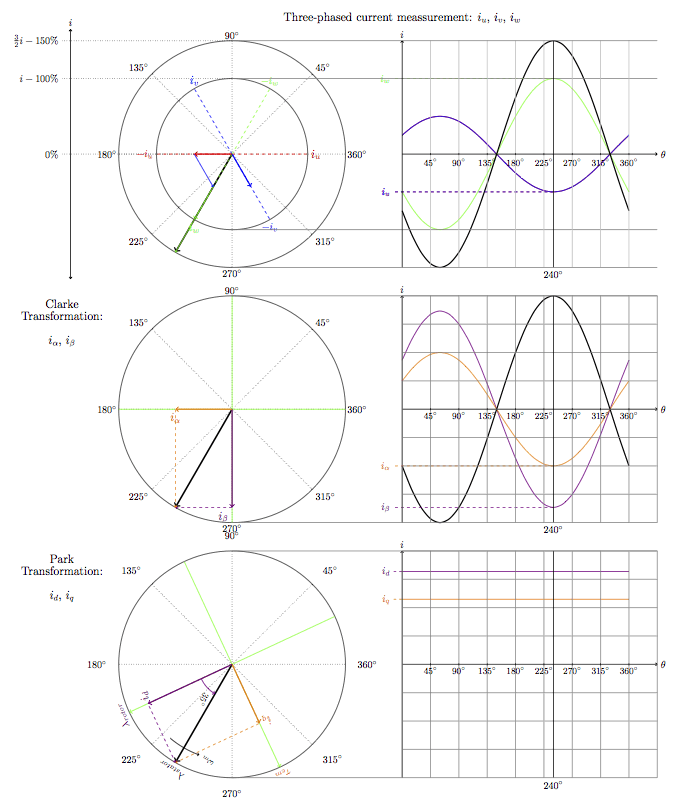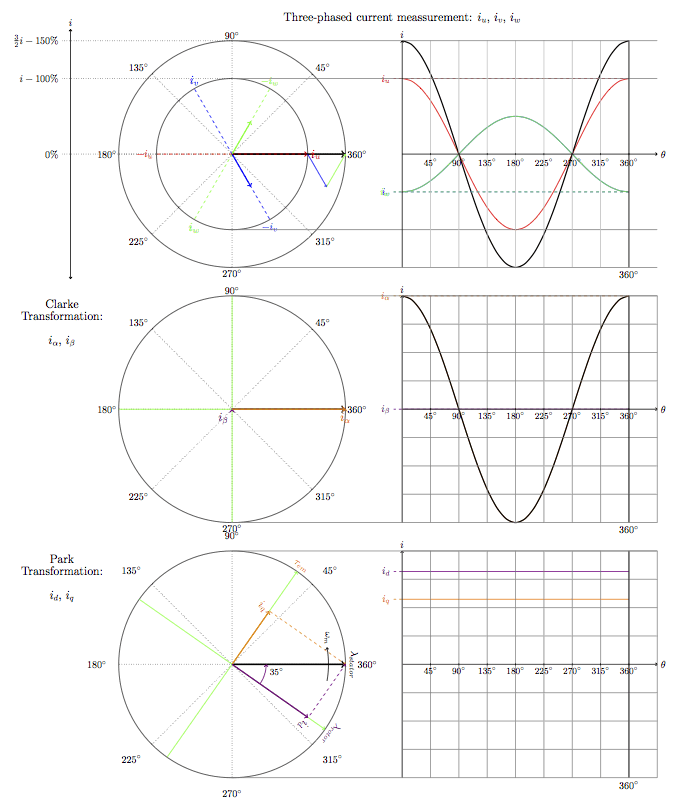
Im obersten Bild werden die drei Statorströme zu einem Raumzeiger zusammengesetzt. Darunter sieht man im mittleren Bild den Statorstrom in Alpha / Beta – Koordinaten. Im untersten Bild sieht man diesen Strom in d/q-Koordinaten.
Weiter