Dieser Teil des Tutorials ist nur für Studierende der ETR prüfungsrelevant.
Bisher haben wir nur Widerstände bei Wechselspannung betrachtet. Betrachten wir als Nächstes Netzwerke aus Widerständen und Speichern. Als Beispiel nehmen wir einen Widerstand und einen Kondensator. Wir rechnen wie im ersten Beispiel im letzten Kapitel.
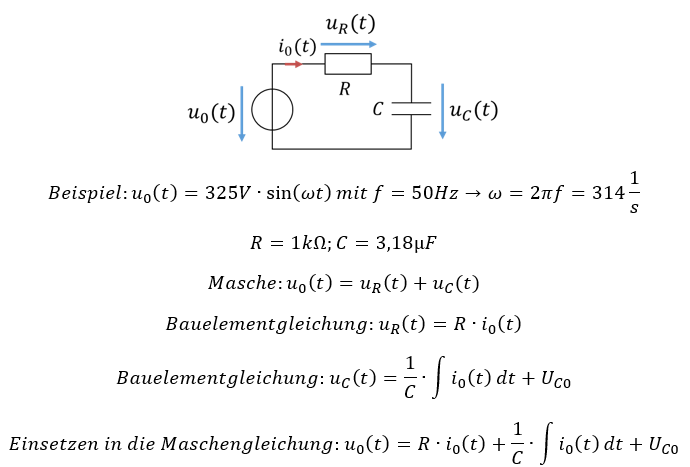
Wir haben innerhalb einer Gleichung den Strom und das Integral über den Strom enthalten. Das bezeichnen die Mathematiker als „Differenzialgleichung“. Sie haben wahrscheinlich noch nicht gelernt, wie Differenzialgleichungen gelöst werden. Selbst wenn Sie es gelernt haben – die Mathematik dafür ist heftig. Wir sind an einem Punkt angekommen, an dem wir mit unserer Mathematik nicht weiterkommen.
Sobald Speicher in einem Wechselspannungsnetzwerk auftauchen, können wir Spannungen und Ströme nicht mehr „von Hand“ berechnen. So lange nur Widerstände im Netzwerk enthalten sind, ist noch alles gut. Der Rest des Kapitels zum Thema Wechselstrom beschäftigt sich mit der Berechnung von Speichern in Wechselspannungsnetzwerken.
Wer versucht, mit Sinus-Größen zu multiplizieren oder zu dividieren, der stellt schnell fest, dass diese Mathematik nicht mehr „von Hand“ gerechnet werden kann. Integrieren und Ableiten von Sinus-Größen ist auch nicht witzig. Selbst das Addieren funktioniert nur, wenn die Phasenwinkel der Sinus-Größen gleich sind. Das ist beim ersten Netzwerk mit den beiden Widerständen der Fall. Simulations-Tools rechnen mit Sinus-Größen. Sie nutzen aber auch mehrere Milliarden Rechenoperationen pro Sekunde dafür, dann ist so eine Integration kein Problem.