Das Rechnen mit Sinus und Cosinus im Zeitbereich ist insbesondere dann unschön, wenn Signalverläufe über der Zeit Integriert oder differenziert werden. Dies ist bei Speichern in einer Schaltung grundsätzlich der Fall, siehe Kapitel Rechnen mit Speichern.
Die Laplace-Transformation bietet auch hier eine deutliche Vereinfachung der Mathematik: Eine Integration über der Zeit im Zeitbereich entspricht im Frequenzbereich einer Division durch Term jω. Eine Ableitung nach der Zeit im Zeitbereich entspricht im Frequenzbereich einer Multiplikation mit dem Term jω.
Für Spannung und Strom am Kondensator lautet die Formel im Zeitbereich (mit uC0 = 0V)
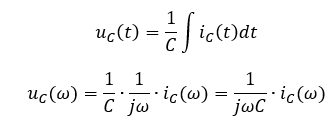
An der Spule können wir den Zusammenhang von Spannung und Strom ebenfalls vereinfachen:
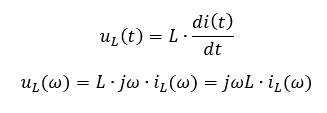
Wir verifizieren die Gültigkeit der Vereinfachung an einer Formel, bei der wir bereits wissen was als Lösung herauskommt. An einem Kondensator gilt bei einer Wechselspannung im Zeitbereich:
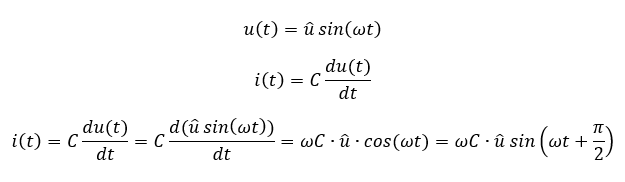
Die Ableitung vom sin(ax) ist a ∙ cos(ax). Dafür brauchen wir die Kettenregel mit der inneren Ableitung. Der Cosinus kann als um π/2 verschobener Sinus ausgedrückt werden. Die Verschiebung um π/2 entspricht einer Multiplikation mit j. Also gilt
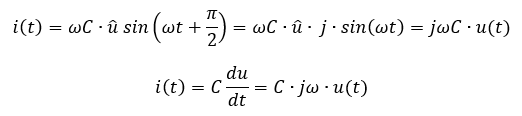
Wir sehen anhand der zeitlichen Ableitung, dass die vorher angenommen Rechnung stimmt.
Achtung: Hier habe ich Zeit- und Frequenzbereich gemischt. Das j gibt es eigentlich im Zeitbereich nicht. Mit dieser etwas unsauberen Vorgehensweise kann dennoch gezeigt werden, dass die Vereinfachungen für Ableitung und Integration stimmen. Wenn Sie das einem Mathematiker zeigen wird er sich die Augen auskratzen, aber es klappt. Für die Integration können Sie den Nachweis selbst versuchen.
Weiter