Wechselstrom mit Speichern

Integration und Ableitung

Wenn wir mit Speichern rechnen, dann müssen wir integrieren oder ableiten. Wie geht das bei sinusförmigen Größen? Es gilt bei einer beliebigen Konstante a:

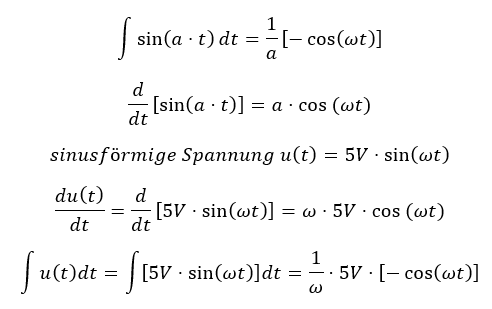
Beim Integrieren und Ableiten ändert sich ein Sinus in einen Cosinus und anders herum. Das ist kein Problem für uns, denn Sinus und Cosinus unterscheiden sich nur dadurch, dass sie zueinander um 90° verschoben sind. Es gilt:

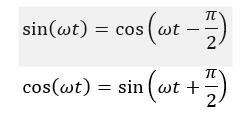
Die Betrachtung der Phase an einem Speicher führt zu einer sehr komplexen Mathematik. Die Reduktion auf die Spitzenwerte kann mit einfacher Mathematik beschrieben werden. Deshalb wird für den Studiengang BMT ab jetzt nur noch der Spitzenwert betrachtet. Wen die komplexe Mathematik interessiert, der muss im Kurs Elektrotechnik für ETR schauen. Das dauert viele Stunden dies nachzulesen – ist aber interessant.

Wenn uns die Verschiebung der Phase egal ist, wir also nur Spitzenwerte betrachten, dann können wir Sinus oder Cosinus fast gleichbehandeln.

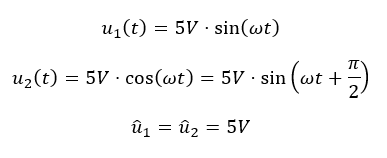
Die Spitzenwerte beider Spannungen sind gleich.

Addition von Sinus und Cosinus

Was passiert, wenn wir beide Spannungen addieren? Man könnte einen Spitzenwert von 10V erwarten, wenn zwei Wechselspannungen mit jeweils 5V Spitzenwert addiert werden. Aus der Grafik der beiden Funktionen erkennt man aber, dass es so einfach nicht ist. Die Summenspannung U_S berechnet sich nach:

In blau ist die Spannung u₁ dargestellt. Sie ist sinusförmig. In rot ist die cosinusförmige Spannung u₂ dargestellt. Die Summe beider Spannungen u₁ + u₂ ist in grau dargestellt. Der Spitzenwert der Summe beträgt nicht die erwarteten 10V, sondern etwas über 7V. Das liegt daran, dass beide Maxima nicht zeitgleich auftreten, so dass niemals 5V + 5V gerechnet wird.

Wir können die Berechnung aus dem Einheitskreis ableiten. Die Länge des schwarzen Pfeils beträgt 1. Er zeigt auf den Umfang des Kreises mit dem Radius 1. Wir können am rechtwinkligen Dreieck aus schwarzem, blauem und rotem Pfeil mit dem Pythagoras und mit Katheten rechnen.

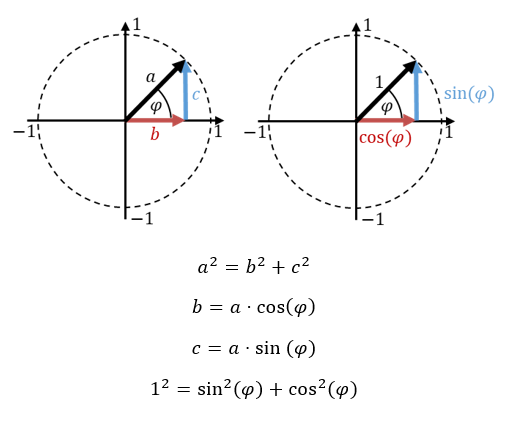
Am Dreieck werden Sinus und Cosinus nicht einfach addiert, sie werden quadratisch addiert. Das nutzen wir für die Spitzenwertberechnung bei Sinus und Cosinus:

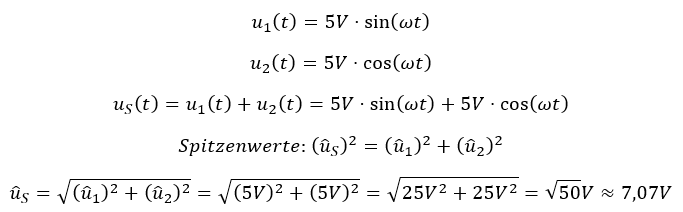
Wir können den Spitzenwert berechnen, nicht aber die Phase der Summenspannung. Wie in der Abbildung unten noch einmal dargestellt ist die Summenspannung verschoben zum Sinus und zum Cosinus. Dieser Verschiebewinkel kann mit der vereinfachten Berechnungsweise nicht ermittelt werden. Man kann das Ergebnis der Summenspannung jetzt so schreiben:

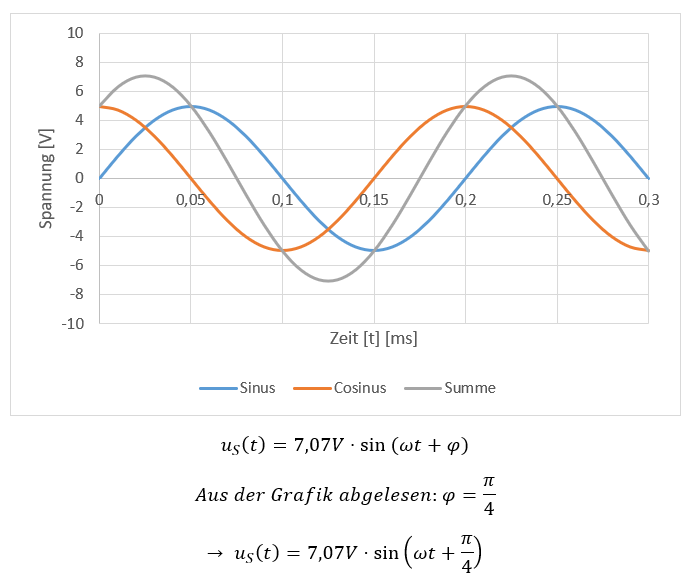
Sie lernen in diesem Kurs nur, die Spitzenwerte zu berechnen. Die Phasen sind nicht prüfungsrelevant. Die Phase im oberen Beispiel wäre anders, wenn die Spitzenwerte nicht zufällig gleich groß gewählt wären. Darauf gehen wir hier nicht weiter ein, Sie sollen nur wissen, dass die Phase nicht immer Pi/4 beträgt.

Merke: Wenn man den Spitzenwert einer Summe zweier Spannungen berechnet, dann muss überprüft werden, ob Sinus oder Cosinus in den Funktionen vorliegen. Wenn zwei Sinus-Spannungen addiert werden, dann werden die Spitzenwerte einfach addiert. Wird ein Sinus mit einem Cosinus addiert, dann werden die Spitzenwerte quadratisch addiert.

Beispiele

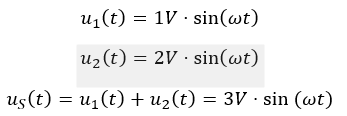
Werden 2 Sinus-Funktionen addiert, werden die Spitzenwerte „normal“ addiert.

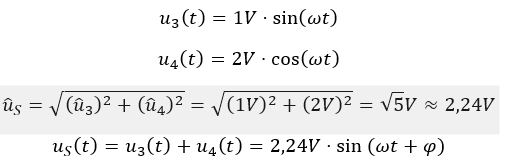
Wird ein Sinus mit einem Cosinus addiert, muss „quadratisch“ addiert werden.

Weiter