Wenn wir magnetisch leitendes Material für die Erzeugung von Feldern für Antriebe nutzen, haben wir einen gewaltigen Hebel zur Optimierung in der Hand. Der Wert von µ
Der Parameter µ
Welche Materialeigenschaft führt dazu, dass die magnetische Flussdichte bei fester magnetischer Feldstärke so viel größer wird? Magnetisch leitfähiges Material besteht aus winzig kleinen magnetischen Dipolen. Das sind Mini-Magnete innerhalb des Materials, die die beiden magnetischen Pole Nordpol und Südpol aufweisen. Das Material besteht aus winzigen Elementarmagneten, die auch als „Weiß´sche Bezirke“ bekannt sind. Diese weisen jeweils einen magnetischen Nordpol und einen magnetischen Südpol auf. Jeder Elementarmagnet ist von einem speziellen magnetischen Feld umgeben.
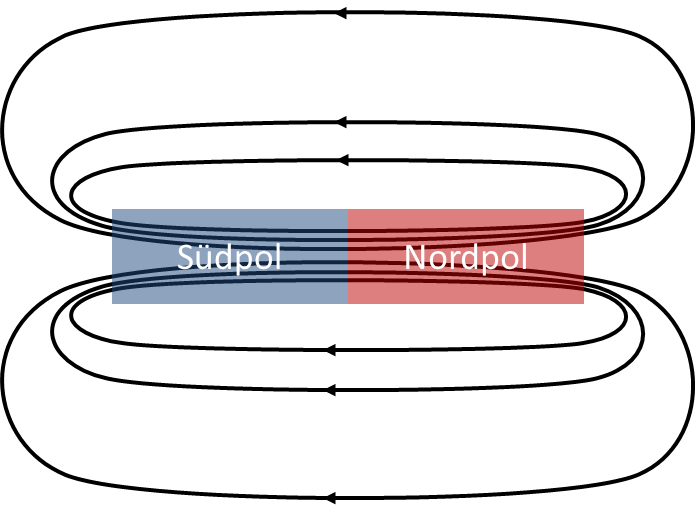
Die Elementarmagnete erzeugen nur magnetische Flussdichte B. Sie weisen ein sehr hohes µr auf. Es gibt in diesem Feld im Inneren des Elementarmagneten nahezu keine magnetische Feldstärke. Ein Elementarmagnet verhält sich analog zu einer elektrischen Stromquelle, an der die Spannung U = 0V anliegt. Magnetische Feldlinien sind allerdings immer geschlossen. Deshalb müssen sie durch Luft hindurch geschlossen werden. Sobald eine Feldlinie durch Luft verläuft, gibt es eine magnetische Feldstärke.

In Luft sind magnetische Feldlinien vom Nordpol zum Südpol gerichtet. Oft werden nur die Feldlinien außerhalb des Magneten dargestellt, weil sich nur dort ein nennenswertes H-Feld einstellt.
Ein Beispiel für magnetisch leitfähiges Material ist z. B. Eisen. Eisen ist zunächst nach außen nicht magnetisch, Sie können damit keine Kraft ausüben. Im Inneren besteht es aber aus vielen Elementarmagneten, die alle zufällig in irgendeine Richtung ausgerichtet sind.

Da sich die B-Felder aller Elementarmagneten überlagern, löschen sie sich aufgrund der zufälligen Ausrichtung gegenseitig aus. Wir halten jetzt das Stück Eisen in ein magnetisches Feld. Dann richten sich die Elementarmagnete im Eisen in Richtung des äußeren Felds aus. Es braucht Energie, um die Elementarmagneten zu drehen, denn sie sitzen fest in einer Struktur. Sie drehen sich nur gegen einen mechanischen Widerstand. Sie drehen sich i. A. nicht vollständig in Feldrichtung.
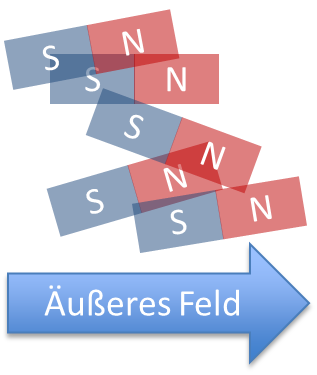
Wenn wir anschließend das äußere Magnetfeld wieder entfernen, bleiben viele der Elementarmagneten ausgerichtet. Sie verhaken sich mechanisch in der neuen Position ineinander, so dass erneut Energie notwendig wäre, sie wieder zurückzudrehen. Durch diese Ausrichtung erzeugt die Überlagerung aller Elementarfelder ein nach Außen wirksames magnetisches Feld des Eisenstücks: Das Stück Eisen ist selbst zu einem Permanentmagneten geworden. Es erzeugt jetzt selbst ein Feld, da die Elementarmagnete sich makroskopisch wie ein einziger Magnet verhalten.
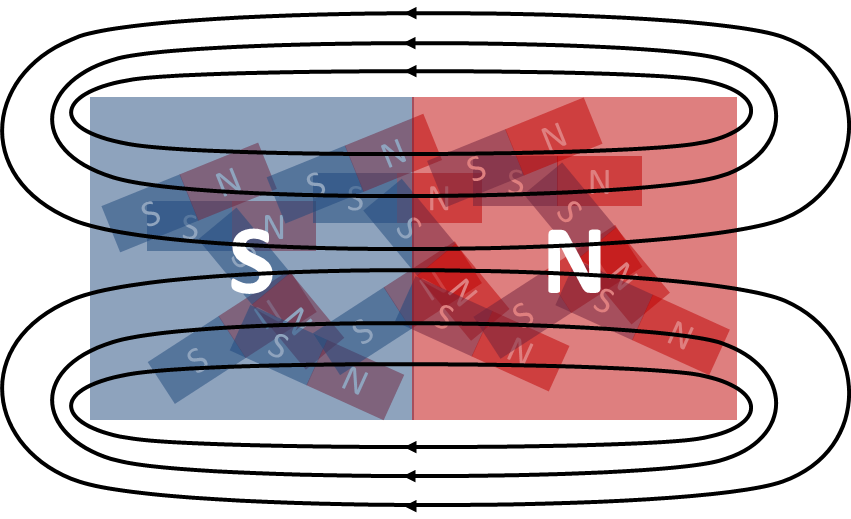
Das Magnetfeld verhält sich genauso wie das eines Elementarmagneten. Im Inneren gibt es fast kein H-Feld und fast nur B-Feld. Im Außenbereich sind B- und H-Feld vorhanden.
Mit dem neuen Magneten können Sie andere Eisenstücke anziehen. Da das Eisenstück dauerhaft magnetisch bleibt, sprechen wir von einem Permanentmagneten. Das Feld einer Spule existiert nur so lange, wie Strom fließt, deshalb ist dies kein permanentes Feld.
Betrachten wir jetzt den Parameter µr genauer. Es gilt:
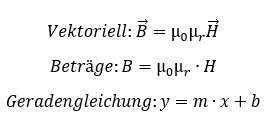
Die Parameter µ0∙µr gibt also die Steigung m an, wenn wir B über H eines magnetisierbaren Materials zeichnen. µ0 ist konstant. Spannend ist der Parameter µr. Dazu betrachten wir eine Spule mit einem Eisenkern.
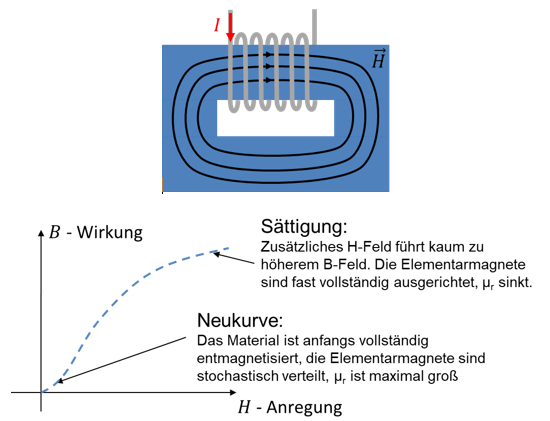
H auf der X-Achse wird als Anregung bezeichnet, weil wir mit einem Strom zunächst ein H-Feld erzeugen. Auf der Y-Achse ist B als Wirkung bezeichnet, weil B sich als Folge der magnetischen Leitfähigkeit einstellt.
Zu Beginn der Betrachtung ist das Material (z. B. Eisenblock) nicht magnetisiert. Alle Elementarmagneten sind stochastisch ausgerichtet. Es fließt kein Strom und es gibt kein Feld. Wir sind am Punkt B = 0 und H = 0 im Diagramm.
Anschließend wird der Strom in der Spule erhöht. Es bildet sich ein H-Feld im Kern, das proportional zum Strom ist. Aufgrund des H-Felds richten sich die Elementarmagneten im Eisenkern aus. Je größer das H-Feld ist, desto mehr Elementarmagneten drehen sich. Dadurch steigt das B-Feld an. Wird H noch weiter erhöht, drehen sich kaum noch Elementarmagneten in Feldrichtung, weil fast alle bereits ausgerichtet sind. B wird nur noch sehr langsam größer, wenn H weiter erhöht wird. Jetzt sind wir rechts oben im Diagramm.
Durch das Ausrichten der Elementarmagnete im Kern ändert sich das H-Feld nicht. Da die Feldlinien im Kern nicht durch Luft gehen, erzeugen sie kein nennenswertes H-Feld. H wird trotz Kern nur vom Spulenstrom vorgegeben.
Jetzt wird der Strom abgeschaltet. Das H-Feld der Spule erlischt, es gilt H = 0. Die Elementarmagnete drehen sich leicht zurück. Sie bleiben aber zu einem Teil in der neuen Position ausgerichtet. Deshalb bleibt ein B-Feld im Kern erhalten. Das B-Feld hat kein H-Feld zur Folge. Die verbleibende magnetische Flussdichte wird als „Remanenzflussdichte“ BR bezeichnet.
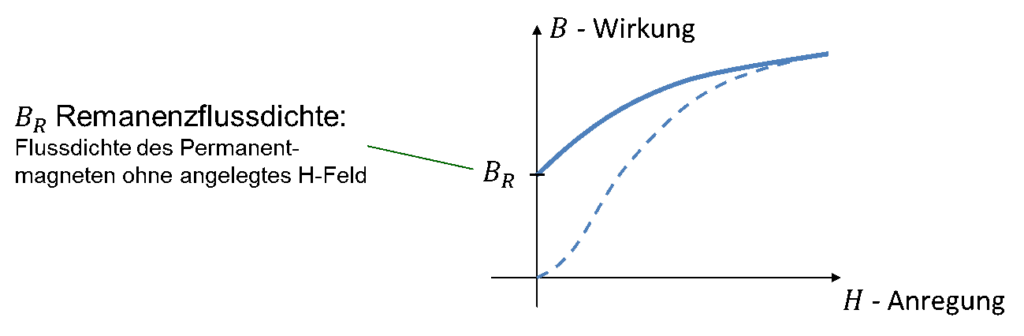
Es ist möglich, den Kern zu entmagnetisieren. Dafür wird ein H-Feld benötigt, das in die andere Richtung zeigt. Drehen wir die Stromrichtung um, dreht sich auch die Richtung des H-Felds um. Dadurch werden die Elementarmagnete so weit zurückgedreht, dass wieder eine stochastische Ausrichtung vorliegt. Das H-Feld, das nötig ist, um den Kern vollständig zu entmagnetisieren, wird als Koerzitivfeldstärke HC bezeichnet.
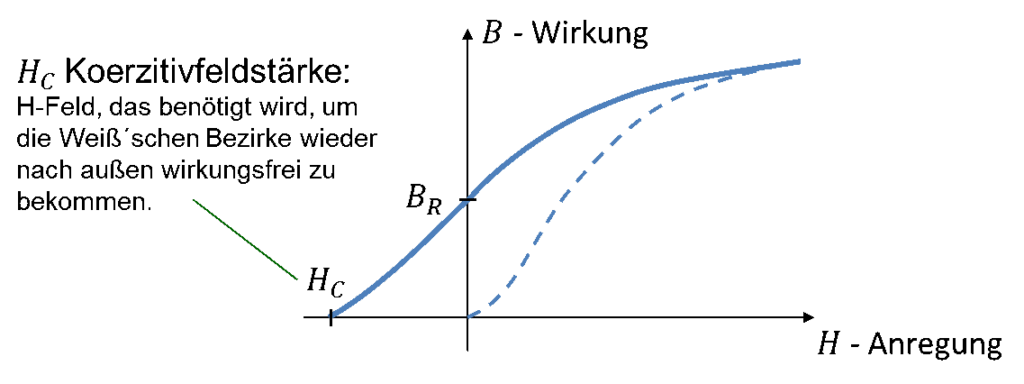
Wird das H-Feld weiter in negative Richtung erhöht, drehen sich die Elementarmagnete weiter in die Richtung des Felds. Auch in diese Richtung weist der Kern eine Sättigung auf. Der Kern ist symmetrisch bezüglich der Strom- und Feldrichtung. Deshalb ergibt sich das folgende Diagramm:

Wenn der Strom langsam von I = 0A bis zum maximalen Strom aufgedreht wird, gelangen wir auf der gestrichelten Neukurve in die rechte obere Ecke des Diagramms. Ändert sich der Strom anschließend langsam auf den maximal negativen Wert, wandern wir entlang der oberen blauen Linie in die linke untere Ecke des Diagramms. Wenn der Strom anschließend wieder bis zum positiven Maximum erhöht wird, laufen wir die untere blaue Kurve entlang in die obere rechte Ecke. Wir müssen die Kurve nicht vollständig durchlaufen. Es ist auch möglich, z. B. immer nur positiven Strom an- und abzuschalten. Dann bewegen wir uns immer entlang der oberen blauen Kurve von links nach rechts.
Die magnetische Flussdichte einer Kernspule ist also abhängig vom Strom, der das H-Feld bestimmt. Sie ist zusätzlich abhängig davon, auf welchem Punkt der Kennlinie wir waren, bevor der Strom eingeschaltet wurde. Waren wir vor der Bestromung auf der oberen Remanenzflussdichte, bewirkt ein positiver Strom nur wenig B-Änderung über BR hinaus. Waren wir auf der unteren Remanenzflussdichte der unteren Kurve, steigt das B-Feld viel stärker an. Es ist zunächst negativ und ändert dann das Vorzeichen. Das B-Feld ist also abhängig von seiner zeitlichen Vergangenheit. Das Verhalten von B-Feld und H-Feld weist eine Hysterese auf.
Bei einer Luftspule ohne Kern gilt µr = 1. Wird bei einer Luftspule der Strom eingeschaltet, stellt sich das gleiche ein H-Feld wie bei einer Kernspule ein. Aufgrund der magnetischen Leitfähigkeit der Luft stellt sich ein kleines B-Feld ein. Zum Vergleich sind unten zwei Verläufe einer Luft- und einer Kernspule dargestellt.
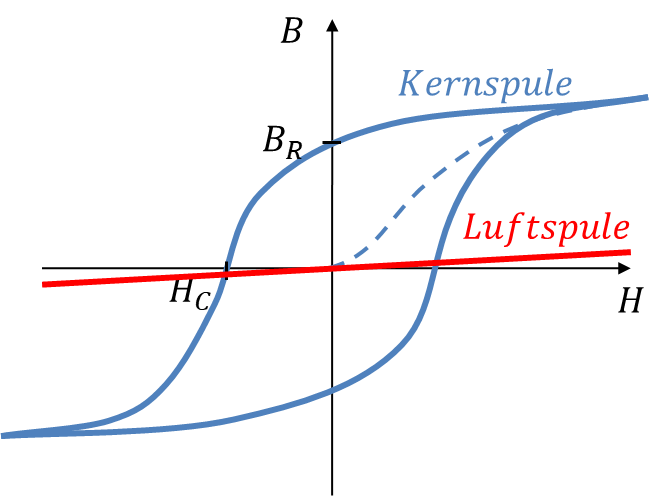
Das B-Feld der Spule mit Kern ist deutlich größer als das der Luftspule. Die Steigung des Verlaufs von B über H ist der Term µ0 ∙ µr. Bei der Luftspule ist die Steigung konstant. Bei der Kernspule ist offenbar µr keine Konstante. Es für Berechnungen von Hand nahezu unmöglich ist zu wissen, welchen Wert B bei gegebenem H annimmt, weil B immer von der Vergangenheit des Felds abhängt. Deshalb verwenden wir für händische Berechnungen erneut eine ziemlich heftige Näherung: Wir setzen einen konstanten Wert für µr für einen Kern an, obwohl die Steigung des B-H-Verlaufs sich – je nach Arbeitspunkt – sehr stark ändert.
Spätestens hier muss jedem klar sein, wie unsinnig es ist, von Hand genaue Feldberechnungen nach unseren Formeln durchzuführen. Alle Formeln, die Sie für Feldberechnungen an Spulen finden, sind ziemlich schlechte Näherungen. Wir dürfen nähern, nur dürfen wir dann nicht so tun, als wäre das Ergebnis genau. Es dient immer nur der Plausibilisierung einer Simulation.
Sie müssen einen Permanentmagneten immer zuerst magnetisieren. Das Material alleine ist magnetisierbar, aber es ist im Rohzustand noch kein Magnet. Die Magnetisierung erfolgt entweder mit einer stromdurchflossenen Spule oder mit einem anderen Magnet, den Sie in die Nähe des zu magnetisierenden Materials halten. Einen Kern können wir auch mechanisch entmagnetisieren. Dazu setzen wir ihn heftigen Erschütterungen aus, die die Elementarmagnete wieder stochastisch ausrichten. Wenn Sie einen Permanentmagneten heftig auf den Boden werfen, wird er einen Teil seiner Magnetkraft verlieren.
Verschiedene Kerne aus unterschiedlichem Material weisen unterschiedliche Werte von HC und BR auf. Diese Parameter charakterisieren einen Kern bzw. magnetisch leitfähiges Material. Wenn Sie einen guten Permanentmagneten bauen wollen, dann muss BR groß sein. Schließlich soll der Permanentmagnet ohne äußeres Feld ein hohes B-Feld aufweisen. Der Kern sollte auch ein großes HC aufweisen. Sonst würden schon kleine äußere Felder sein B-Feld abbauen. Ein guter Permanentmagnet weist prinzipiell folgenden B-H-Verlauf auf:
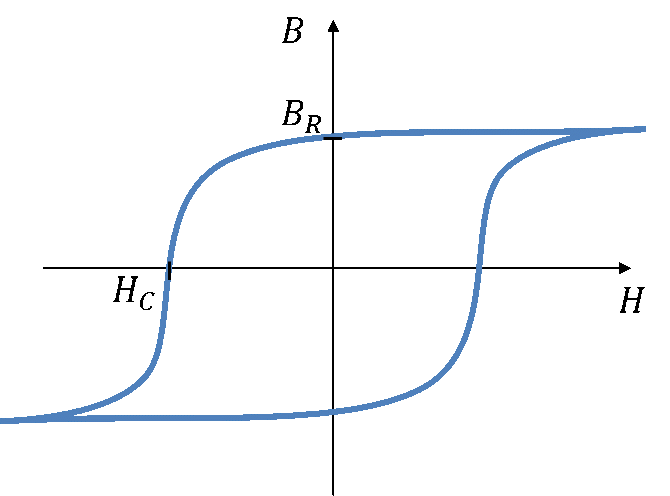
Ein möglichst linearer Kern (lineares µr), der ohne Spulenstrom gar kein Permanentmagnet sein soll, weist eher so einen B-H-Verlauf auf:
